非线性系统的混沌特性分析方法–相图/分岔图分析法
混沌映射被用于生成混沌序列,这是一种由简单的确定性系统产生的随机性序列。一般混沌序列具有以下主要特征:
- 非线性;
- 对初值的敏感依赖性;
- 遍历性;
- 随机性;
- 奇异吸引子(混沌吸引子);
- 分数维持性;
- 整体稳定局部不稳定;
- 长期不可预测性;
- 轨道不稳定性及分叉;
- 普适性和Feigenbaum常数。
由于非线性系统的动力学特性的复杂性,如何判断非线性系统中的混沌行为,一直是混沌学研究的重要课题。一般地,判断系统混沌特性的方法有相轨线(相图)分析法、自功率谱分析法、Lyapunov特征指数法、分数维分析法、分频采样法、赝相空间法、Poincare截面法、0-1测试法和复杂度测度法等。
非线性系统一般有两种类型,离散混沌系统与连续混沌系统,绘制的相图的方法,主要是通过求解微分方程的数值解,常用的是简单的欧拉法,龙格库塔方法等。
相图分析法
相图分析法是一种直接观测法,混沌运动的往复非周期运动特性可以利用相平面图的几何方法表示出来。周期运动每隔一个周期就要重复以前的运动,其运动的相轨迹曲线是一条封闭的曲线。混沌运动是非周期性运动,因而混沌运动的相轨迹曲线是一条永远不封闭的曲线,而运动的往复型则反映在相轨迹曲线局限于一个有界的区域内,不会发散到无穷远,也不会收敛于稳定点,从而形成奇异吸引子。所以,如果对非线性系统进行仿真,画出系统的相图,就可以直观地初步确定非线性系统的动力学行为,包括极限环、周期运动和混沌运动等。相轨线图的缺点是,当周期运动的周期很长时,仅根据相平面图难以准确区分周期运动和混沌运动。
混沌吸引子具有复杂的拉伸、折叠和伸缩的结构,使得按指数规律发散的系统保持在有限的空间内,它是动力学系统整体稳定性和局部不稳定性共同作用的结果。由于整体的稳定性,时的一切位于吸引子之外的云动都向吸引子靠拢,运动轨道收敛到吸引子上;而局部的不稳定,使得一切到达吸引子内部的运动轨道相互排斥,在某些方向上发散,成为不稳定的因素。微小的扰动对混沌吸引子来说都是稳定的,终将到达吸引子上。但是,在混沌吸引子内部,系统运动状态对初始条件非常敏感,即进入混沌吸引子的位置稍有差别,随着时间演化,这一差别会以指数形式增长,最终导致混沌轨道的截然不同。混沌吸引子又具有分形性质,是一个分形集;混沌吸引子具有无穷嵌套的自相似结构;混沌吸引子具有分维性,它是对我们所熟知的整数维空间中维数概念的扩展。
分岔图分析法
当系统参数变化时,其庞加莱映射在某一坐标轴上的投影可构成该参数变化时的分岔图。对于确定不变的系统参数,分岔图上一个信号点或者与系统周期数相等的儿个信号点可以表示系统周期稳定的状态。而混沌图中画出的无数个点则表示出现混沌现象时存在无数个周期信号点从不落到相同的位置上。因此,在分岔图中,可以很清晰地描绘出系统性能随系统参数变化的特征。
离散混沌系统案例
-
分段线性映射
1.1 Tent映射
x n + 1 = { a x n , 0 ≤ x n < 0.5 a ( 1 − x n ) , 0.5 ≤ x n < 1 μ ∈ ( 0 , 2 ] x_{n+1}= \begin{cases} ax_n, 0\le\ x_n \ < \ 0.5\ \\ a(1-x_n),0.5\le\ x_n \ <\ 1\ \\ \mu \in(0,2] \end{cases} xn+1=⎩ ⎨ ⎧axn,0≤ xn < 0.5 a(1−xn),0.5≤ xn < 1 μ∈(0,2]
clc; clear all; close all; axis([0,1,0,1]); %% 初始值 x0=0.1;t=800;M=850; r=0:0.01:1; [m,n]=size(r); hold on for i=1:n if x0<0.5 x(1)=2*r(i)*x0; end if x0>=0.5 x(1)=2*r(i)*(1-x0); end for j =2:M if x(j-1)<0.5 x(j)=2*r(i)*x(j-1); end if x(j-1)>=0.5 x(j)=2*r(i)*(1-x(j-1)); end end xn{i}=x; %%pause(0.1); plot(r(i),xn{i},'b.','Markersize',2); xlabel('r');ylabel('x(i)'); end%% Tent y_2=zeros(1,10^5); y_2(1)= 0.152; Beta = 0.4; for i = 1 : 10^5-1 if (y_2(i)<=Beta && y_2(i)>0) y_2(i+1) = y_2(i)/Beta; else y_2(i+1)=(1-y_2(i))/(1-Beta); end end figure h2=histogram(y_2,200); h2.FaceColor=[0 0 1]; xlim([0,1])%设置x轴范围 xlabel('Tent map')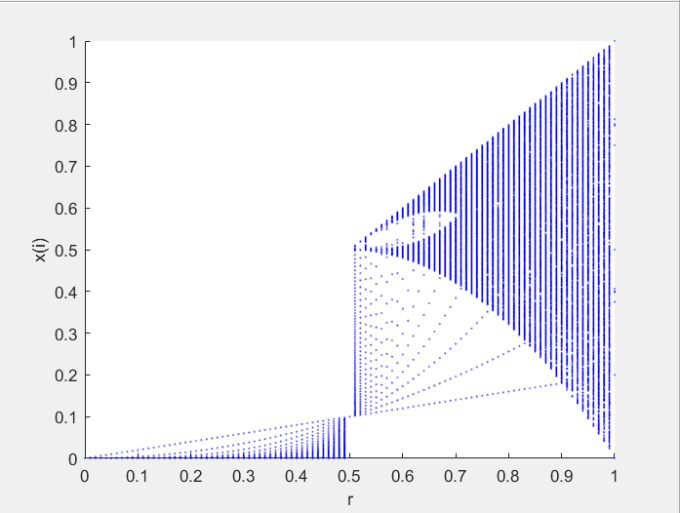

1.2 Bernoulli映射
clc;clear all;close all axis([0,1,0,1]); x0=0.1;t=800;M=850; r=0:0.01:1; [m,n]=size(r); hold on for i=1:n if x0<0.5 x(1)=2*r(i)*x0; end if x0>=0.5 x(1)=2*r(i)*(x0-1)+1; end for j =2:M if x(j-1)<0.5 x(j)=2*r(i)*x(j-1); end if x(j-1)>=0.5 x(j)=2*r(i)*(x(j-1)-1)+1; end end xn{i}=x; %%pause(0.1); plot(r(i),xn{i},'b.','Markersize',2); xlabel('r');ylabel('x(i)'); end

x n + 1 = { a x n , 0 ≤ x n < 0.5 a ( x n − 1 ) + 1 , 0.5 ≤ x n < 1 x_{n+1}=\begin{cases} ax_n,0\le\ x_n\ < \ 0.5\ \\ a(x_n-1)+1,0.5\le\ x_n \ <\ 1\ \\ \end{cases} xn+1={axn,0≤ xn < 0.5 a(xn−1)+1,0.5≤ xn < 1 1.3 抛物线映射(Logistic)
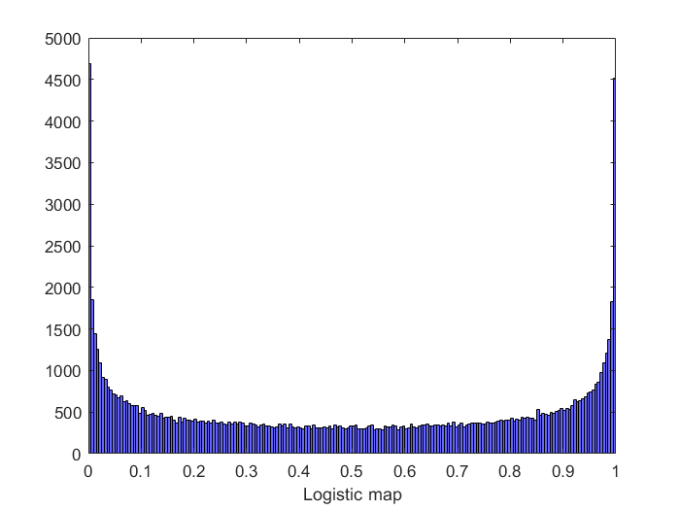
x n + 1 = μ x n ( 1 − x n ) μ ∈ ( 0 , 4 ) x 0 ∈ ( 0 , 1 ) x_{n+1}=\mu x_n(1-x_n)\\ \mu\in (0,4) \\ x_0 \in(0,1) xn+1=μxn(1−xn)μ∈(0,4)x0∈(0,1)
figure(1);
axis([2.7, 4, 0, 1]);
grid
hold on %保持屏幕不动,持续打点
for r = 2.7:0.005:3.9
x = 0.1;
for i =2:200
x(i) = r *x(i-1) *(1-x(i-1));
end
pause(0.1)%暂停函数
for i=151:200
plot(r,x(i),'k.');
end
end
title('Logistic映射分岔图');

- 二维离散送代映射
2.1 Henon映射
{
x
n
+
1
=
1
−
a
x
n
2
+
y
n
y
n
+
1
=
b
x
n
\begin{cases} x_{n+1} = 1-ax_n^2+y_n \\ y_{n+1} = bx_n \\ \end{cases}
{xn+1=1−axn2+ynyn+1=bxn
1.07 ≤ a ≤ 1.4 , b = 0.3 x n ∈ ( − 1.5 , 1.5 ) 1.07\le\ a\le1.4,b=0.3 \\ x_n\in(-1.5,1.5) 1.07≤ a≤1.4,b=0.3xn∈(−1.5,1.5)
当a在这个范围内时,系统处于混沌状态,当a=1.4时,系统的复杂度最大,一般在混沌研究中取a=1.4,b=0.3
clc;
clear all;
a=1.4;
b=0.3;
x(1)=0.5;
y(1)=0.5;
for i=2:1000
x(i)=1-a*x(i-1)^2+y(i-1);
y(i)=b*x(i-1);
end
figure(1)
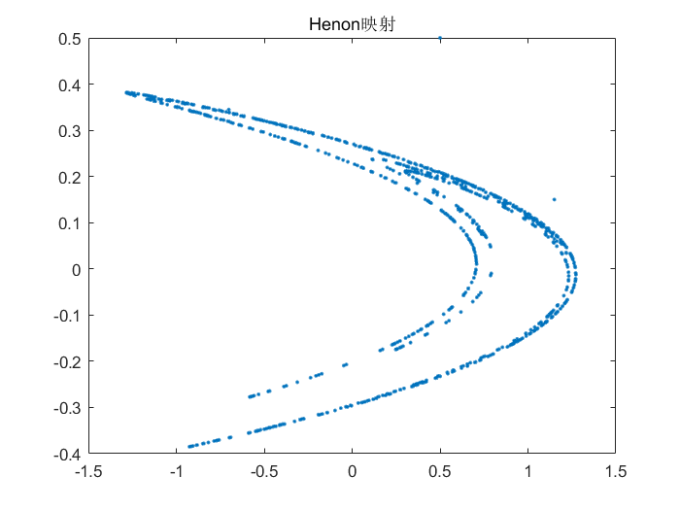
plot(x,y,'.');
title('Henon映射')
clc;
clear all;
figure(1);
axis([0, 1.5, -1, 1]);
grid
hold on
b=0.3;
for a = 0:0.01:1.5
x(1)=0.5;
y(1)=0.5;
for i =2:200
x(i)=1-a*x(i-1)^2+y(i-1);
y(i)=b*x(i-1);
end
pause(0.1)
for i=10:200
plot(a,y(i),'k.');
end
end
xlabel('a');
ylabel('yn');
title('Henon分岔');
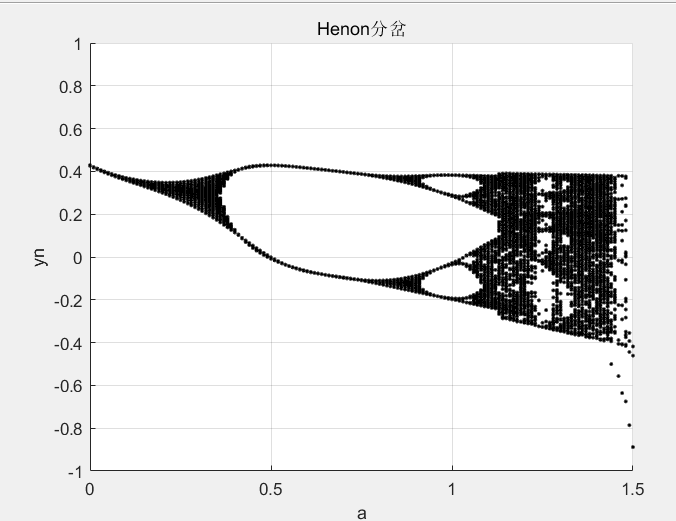
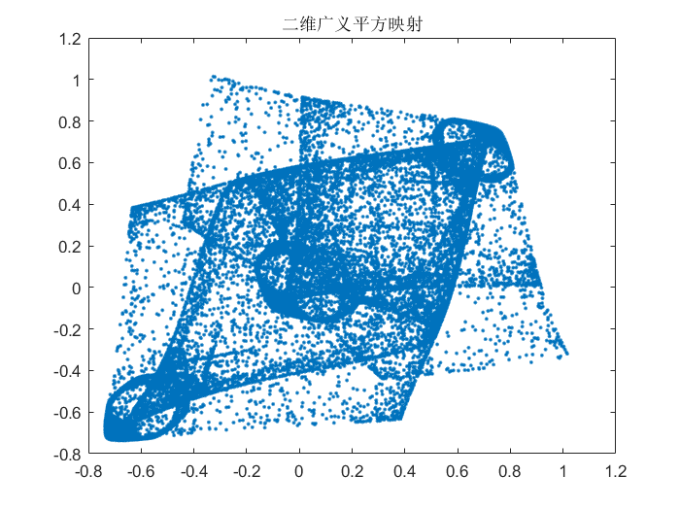
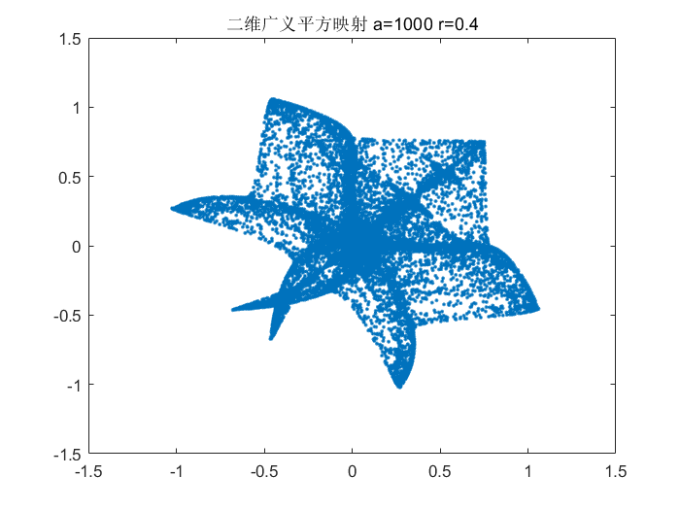
2.2 二维广义平方映射
动力学行为由四个控制参数,r,a, b1, b2决定,若固定参数a=10,选取参数在下面的范围内
r
∈
[
−
1
,
1
]
b
1
=
b
2
=
b
∈
[
−
1
,
1
]
r\in[-1,1] \\ b_1 = b_2 = b \in[-1,1]
r∈[−1,1]b1=b2=b∈[−1,1]
{ x n + 1 = b 1 [ e x p − a x n 2 − x n 2 ] + r y n y n + 1 = b 2 [ e x p − a y n 2 − y n 2 ] + r x n \begin{cases} x_{n+1} = b_1[exp^{-ax_n^2}-x_n^2]+ry_n \\ y_{n+1} = b_2[exp^{-ay_n^2}-y_n^2]+rx_n \\ \end{cases} {xn+1=b1[exp−axn2−xn2]+rynyn+1=b2[exp−ayn2−yn2]+rxn