1.有哪些情况？

今天来实现下小球碰到方块的判定

那么我们首先要明确的就是在什么时候，小球会碰到方块？

1.1 小球在方块左侧

第一个就是小球在方块的左侧的情况：

此时小球圆心的x轴为320，y轴的范围是380~280

1.2 小球在方块上面

第二个是小球在方块上面的情况：

此时小球x轴的变化范围为280~340，y轴为320

1.3 小球在方块右侧

第三个也是最后一个是小球在方块右侧的情况：

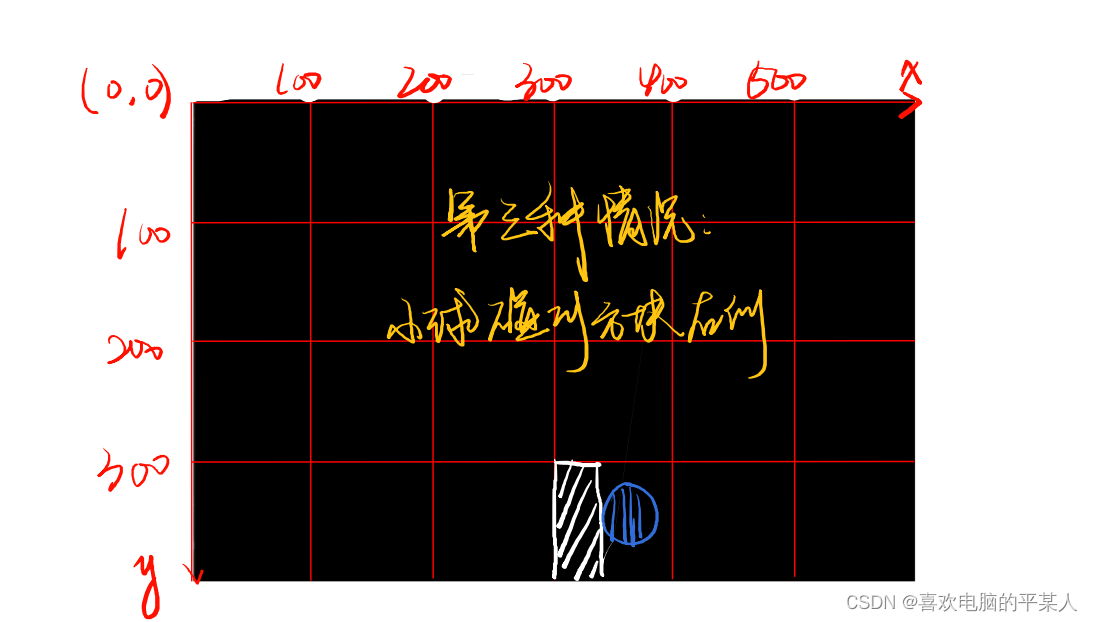
此时小球x轴为340，y轴的变化范围为280~380

2.解决

我们只需写一个if-else语句即可：

if ((rect_left_x <= ball_x + r) && (rect_left_x + rect_width >= ball_x - r)&&(height-rect_height<=ball_y+r)) {
	Sleep(100);
}

也就是碰到方块做一个慢动作的效果
整段代码就是：

#include<graphics.h> 
#include<conio.h>
#include<stdio.h>

int main() {
	double width, height;//定义画面长度、宽度
	width = 600;
	height = 400;
	initgraph(width, height); 

	double ball_x, ball_y,ball_vy, r,g;//定义小球x轴、y轴、y轴方向的速度、半径、重力加速度
	g = 0.6;
	r = 20;
	ball_x = width / 4;//x坐标等于整个画面x轴长度的四分之一
	ball_y = height - r;//y坐标等于画面的y轴长度减去圆的半径（保证圆在画面的最底端）
	ball_vy = 0; //最初小球落在地面上时y轴方向的速度为0

	double rect_left_x, rect_top_y, rect_width, rect_height;//定义方块的各个位置变量
	rect_width = 20;
	rect_height = 100;
	rect_left_x = width * 3 / 4;
	rect_top_y = height - rect_height;

	double rect_vx = -3;//定义方块的移动速度
	while (1){
		if (_kbhit()) {
			char input = _getch();
			if (input == ' ') {
				ball_vy = -16;
			}
		}
		ball_vy = ball_vy + g;//根据牛顿力学定律得
		ball_y = ball_y + ball_vy;//小球y轴方向的变化
		if (ball_y >= height - r) {
			ball_vy = 0;//小球落地以后速度清零
			ball_y = height - r;
		}
		rect_left_x = rect_left_x + rect_vx;
		if (rect_left_x <= 0) {
			rect_left_x = width;//方块消失以后重新出现
		}
		if ((rect_left_x <= ball_x + r) && (rect_left_x + rect_width >= ball_x - r)&&(height-rect_height<=ball_y+r)) {
			Sleep(100);//碰到方块慢动作
		}
		cleardevice();
		fillrectangle(rect_left_x, height - rect_height, rect_left_x + rect_width, height);
		fillcircle(ball_x, ball_y, r);
		Sleep(10);
	}
	_getch();
	closegraph();
	return 0;
}

效果：