x.1 过拟合问题

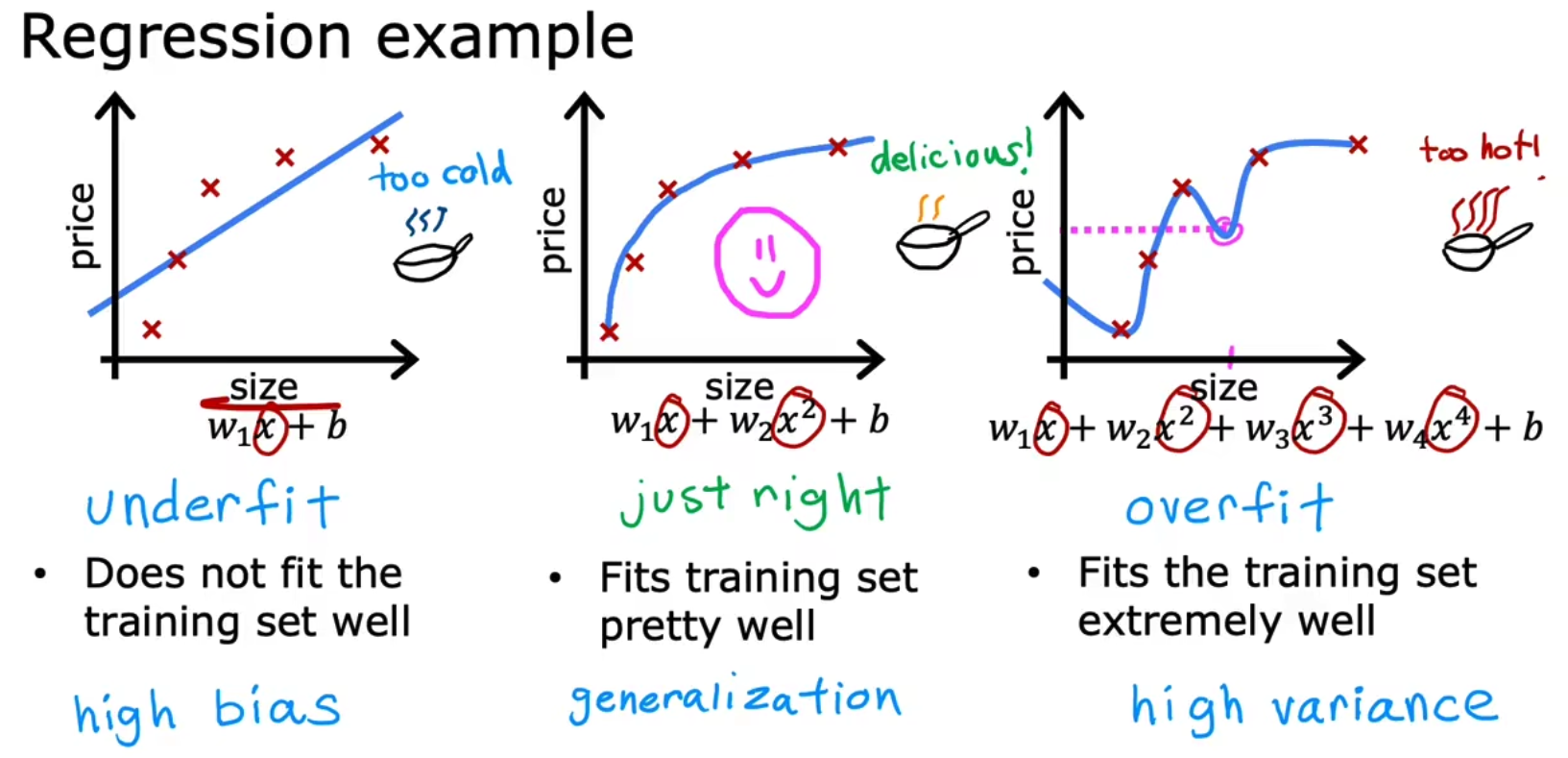
在开始前，让我们先理解一下模型拟合过程中经常出现的三种情况，underfit， just right， overfit/high variance，underfit是指没有足够的特征来拟合现有数据或者iterations训练轮次过少，而overfit是指使用了远大于数据集特征的模型来拟合现有数据。

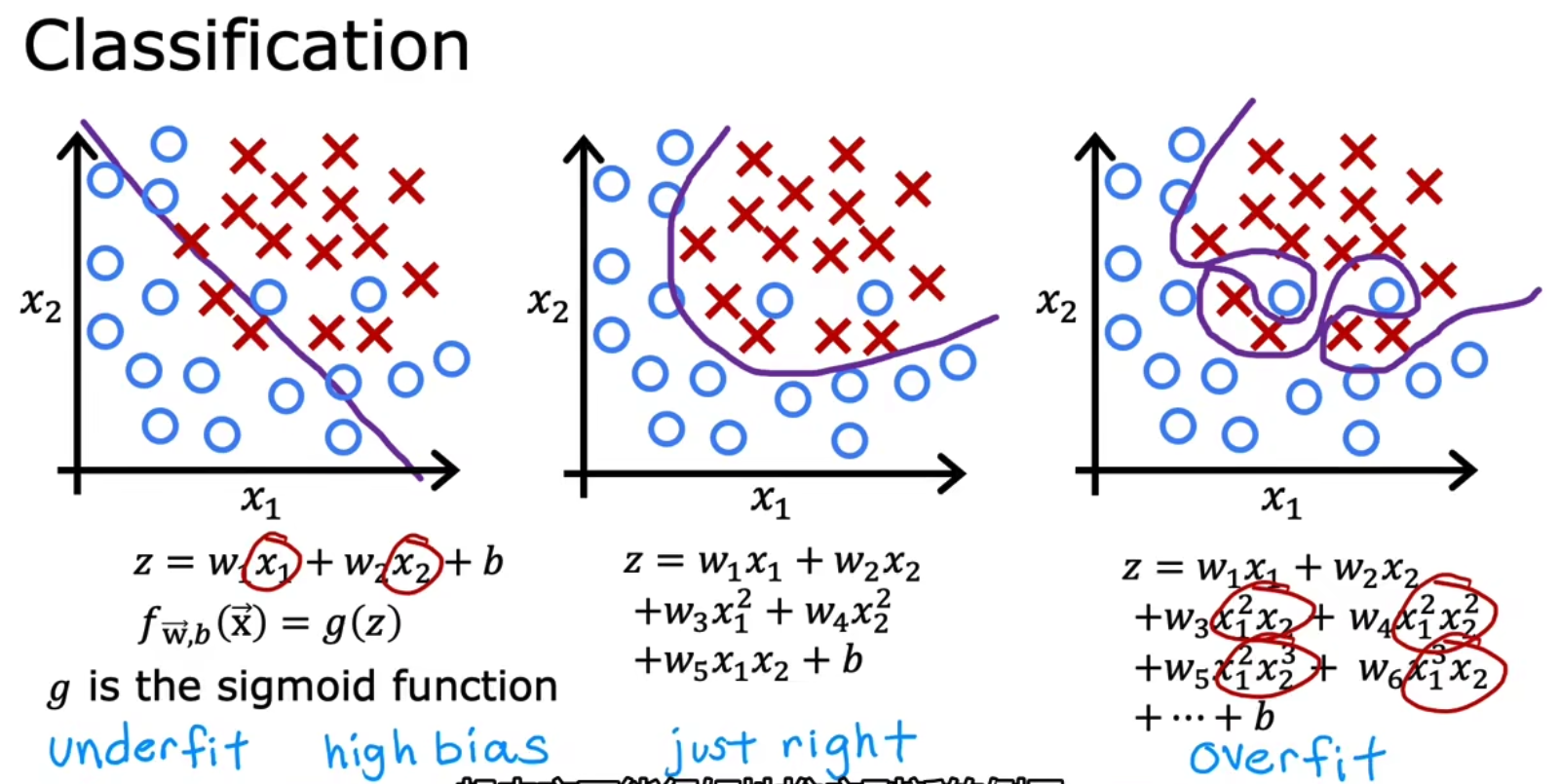
为了更好的理解，让我们再举例一个Classification的例子，

x.2 如何解决过拟合问题

对于解决过拟合问题，其中一个常用的方法是使用更多的training examples训练样本，

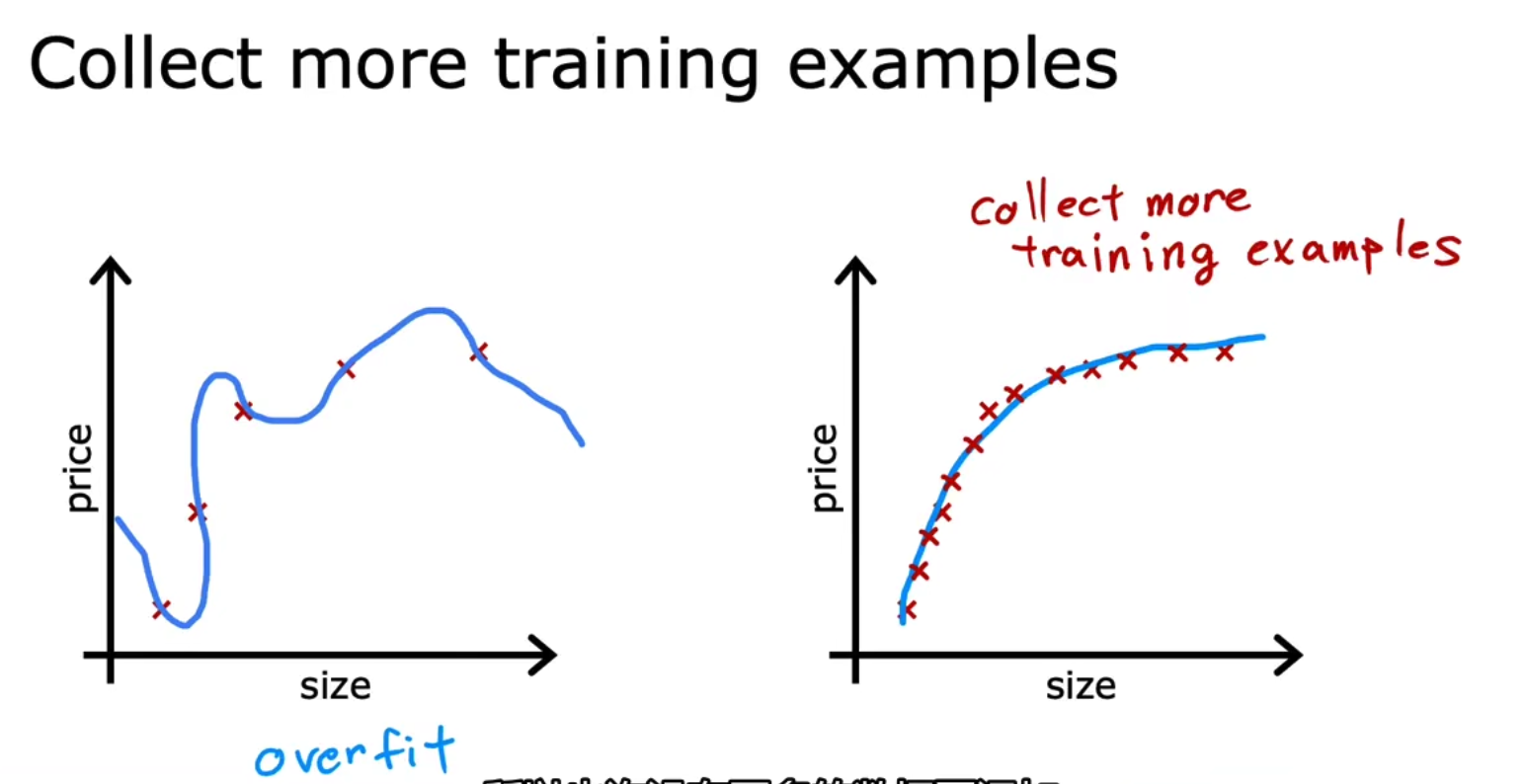
对于解决过拟合问题，我们还有一个方法就是前面提到的特征工程中，进行特征选择的过程，我们可以选择一些直觉上有用的特征以此来达到减少复杂度的目的，当然这种方式也存在一些不好的地方，例如一些有用的特征可能会丢失，

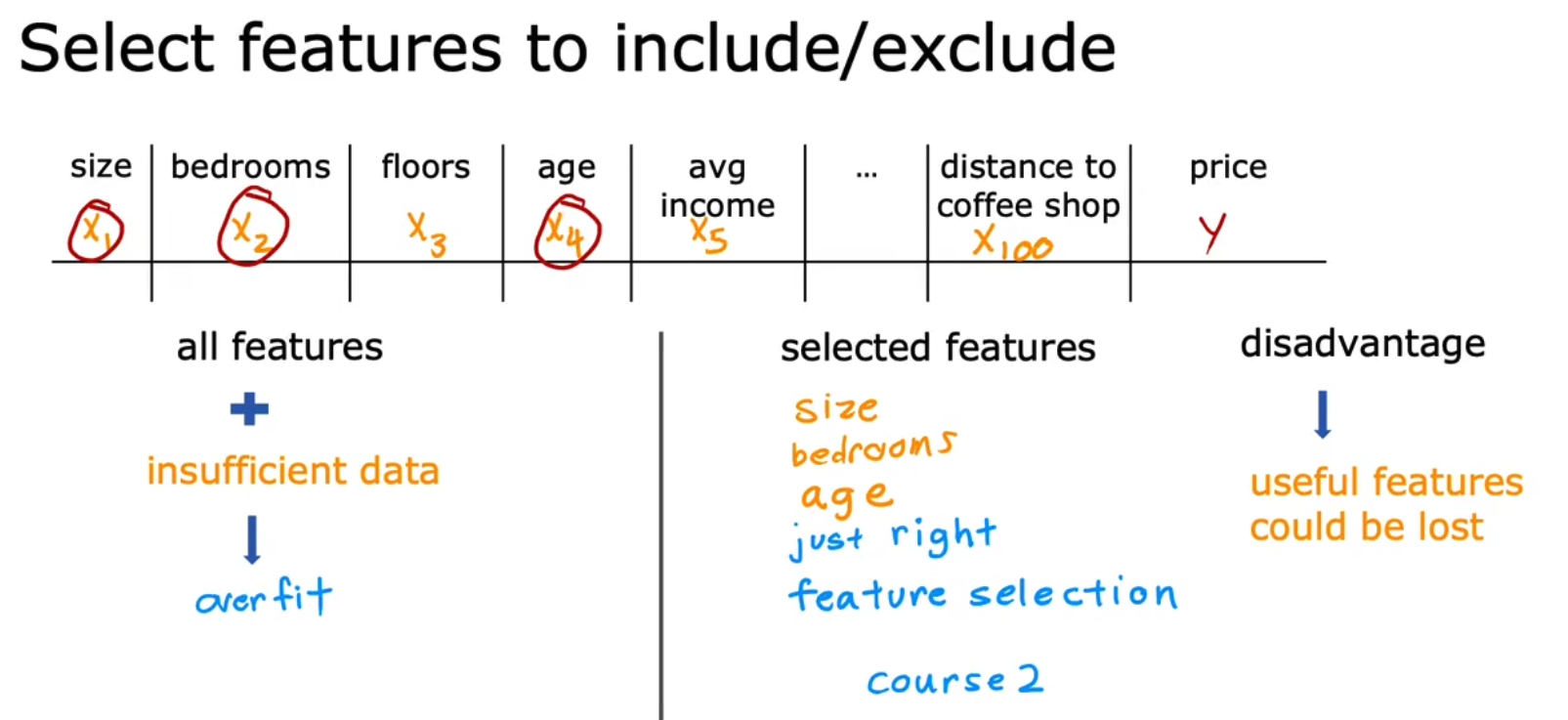
最后一类减少过拟合的方法叫做正则化，而实际上我们最长使用的正则化技术叫做L2正则化，它的原理是通过将部分特征的系数置为一个非常小的数以达到减少特征的作用，如下我们将x四次方的系数设置为0.0001以此达到最小化x四次方对f(x)造成的影响。注意，在实际情况中，我们往往只对weight的值进行L2正则化，而忽视bias，并不对bias的值进行正则化。

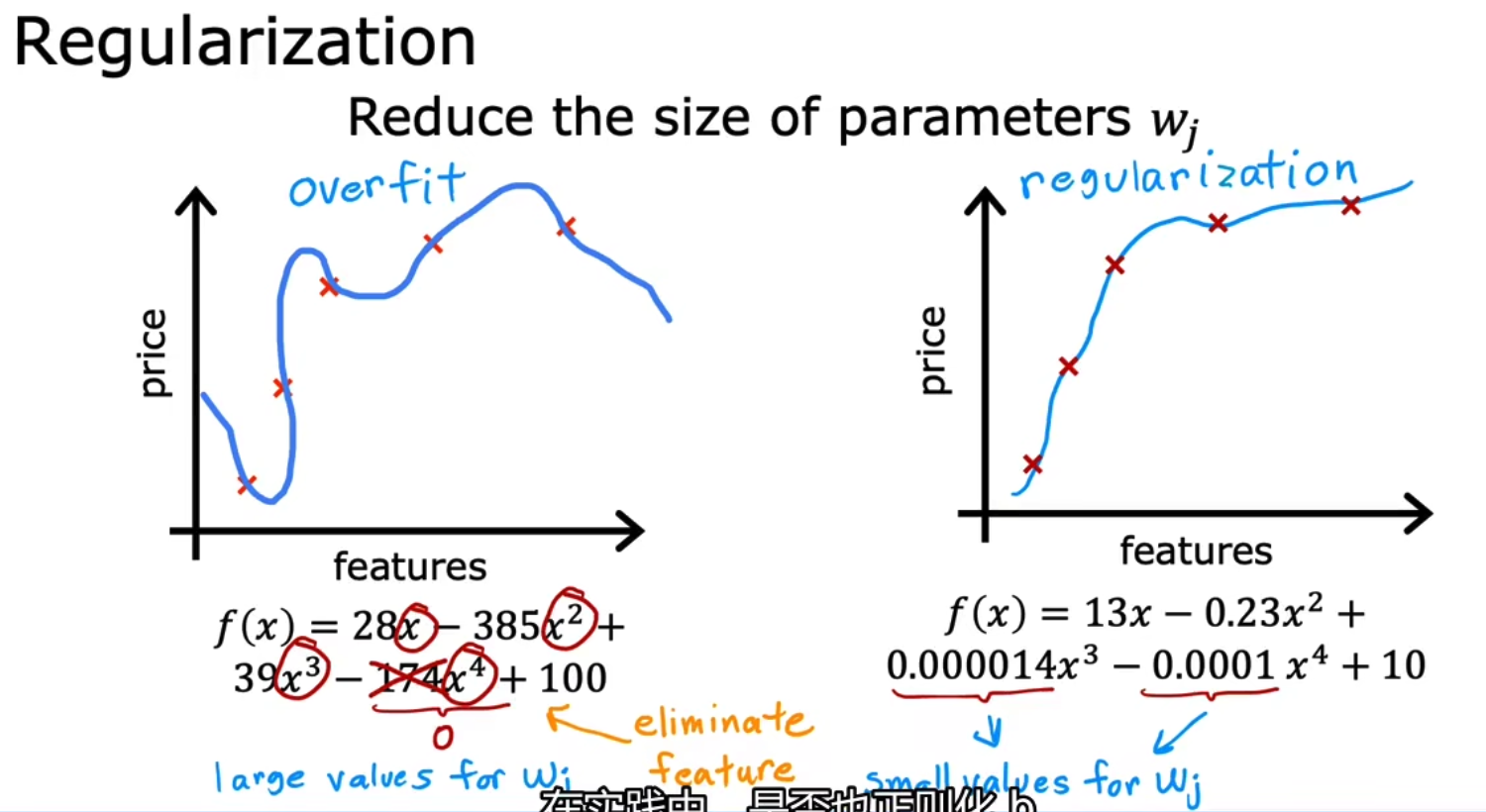
x.3 如何实现L2正则化

实现L2正则化，即将weight权重加入到损失函数中，例如我们不想要x的三次方和x的四次方，我们就把x的三次方和x的四次方前的可学习权重weight加入到我们的loss中，由于我们的策略要做的事情是argmin(loss)，所以我们便会想方设法使得w3和w4小，如下，

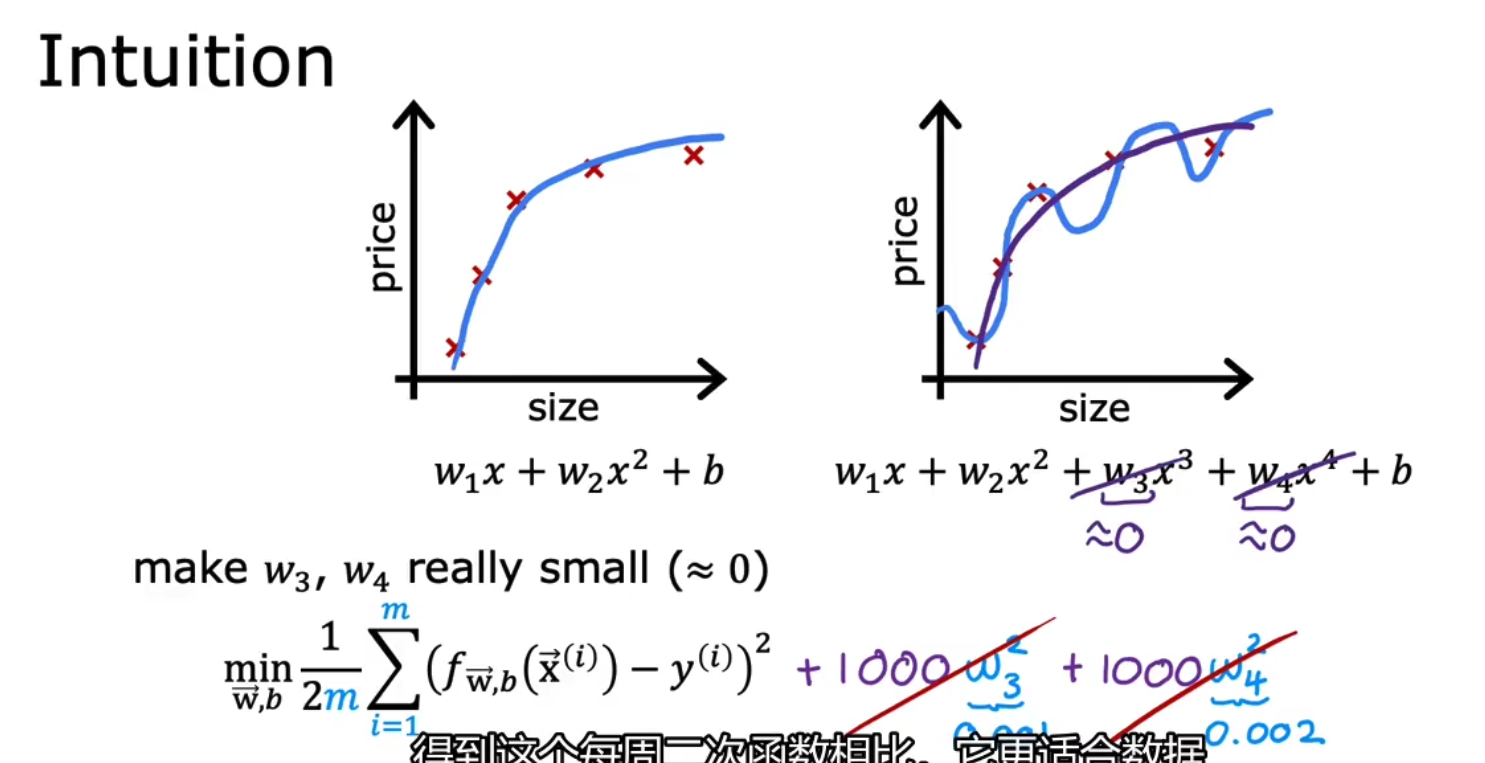
但是往往你并不知道你需要对哪一个特征进行惩罚，所以我们一视同仁地对这些特征进行惩罚，即我们对所有的特征都进行惩罚如下，其中我们往往只对weight进行惩罚而忽视bias，这种全部惩罚的方式被实验证明是极好的。

我们对下面式子的直观理解是，当lambda=0时，等于不添加对权重的乘法，会偏向于overfit过拟合；而当lambda=无穷大时，几乎就等于将权重值全部置为0，会偏向于underfit欠拟合。所以lambda要合适的选择，用于权衡data和weight中的平衡。

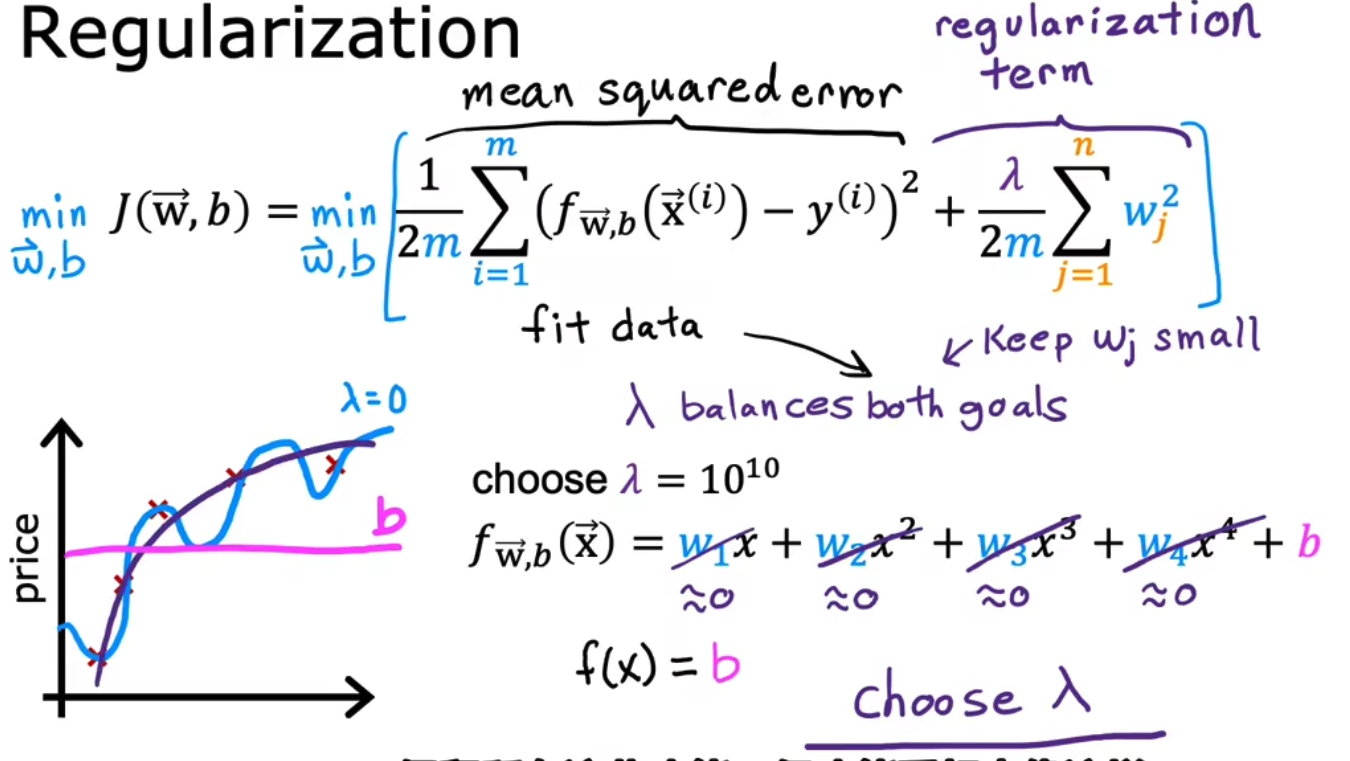
x.4 将L2正则化应用于Linear Regression

接下来我们将梯度下降算法应用于更新的loss，由于我们只增加了对weight的惩罚，所以wj的偏微分会产生变化，如下所示，

针对wj的变换，我们做恒等变换得到$wj(1-\alpha \ast \lambda /m)+...$，我们能够发现省略号…中的部分是不变的，即我们的L2正则化其实只改变了wj前的系数，例如wj * 0.9998，正则化本质上只做了shrink weight缩小权重的作用。

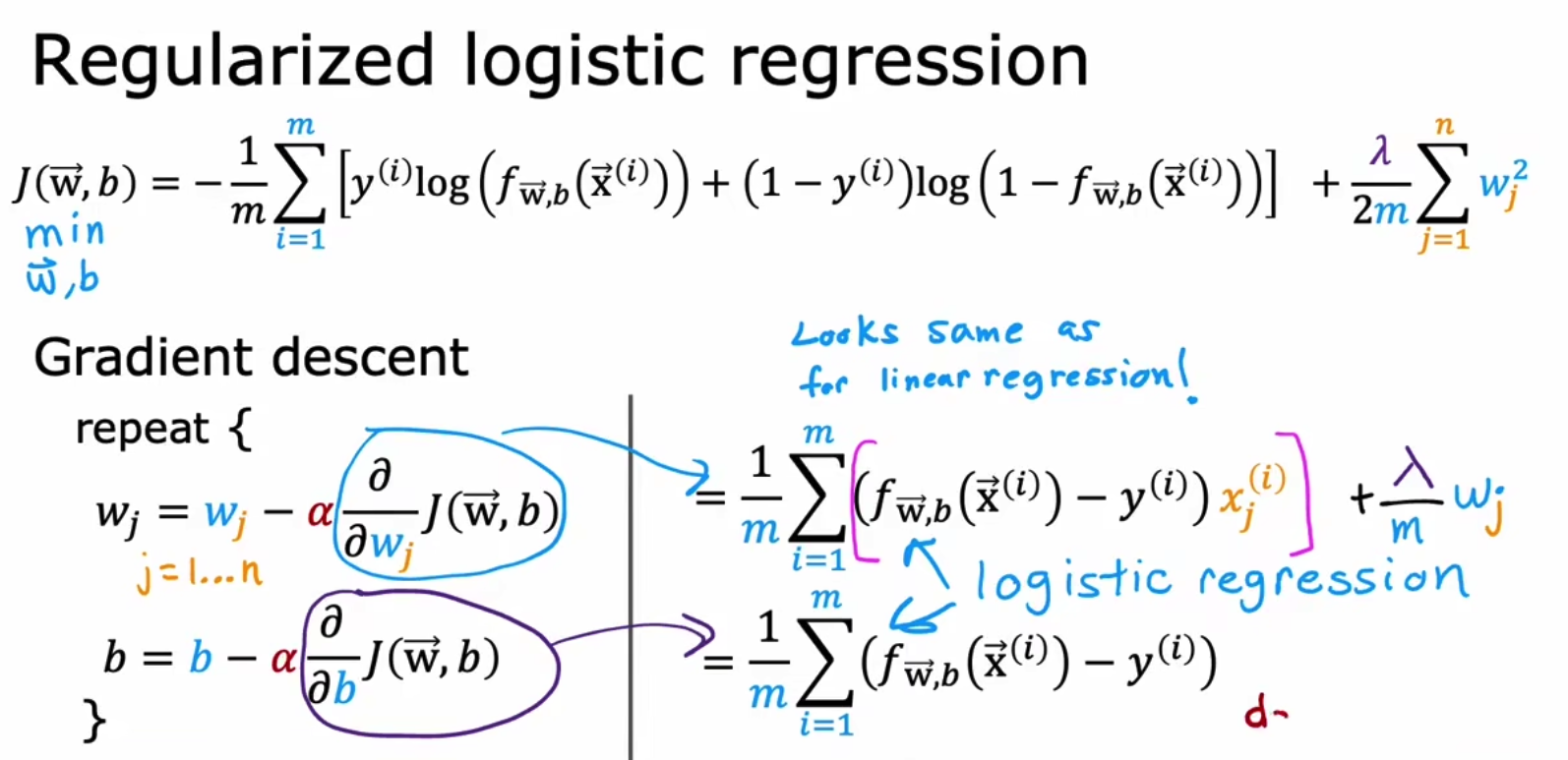
x.5 logistic regression

同样也可以将L2正则化应用于逻辑回归，和线性回归类似，只不过f(x)产生了变化，