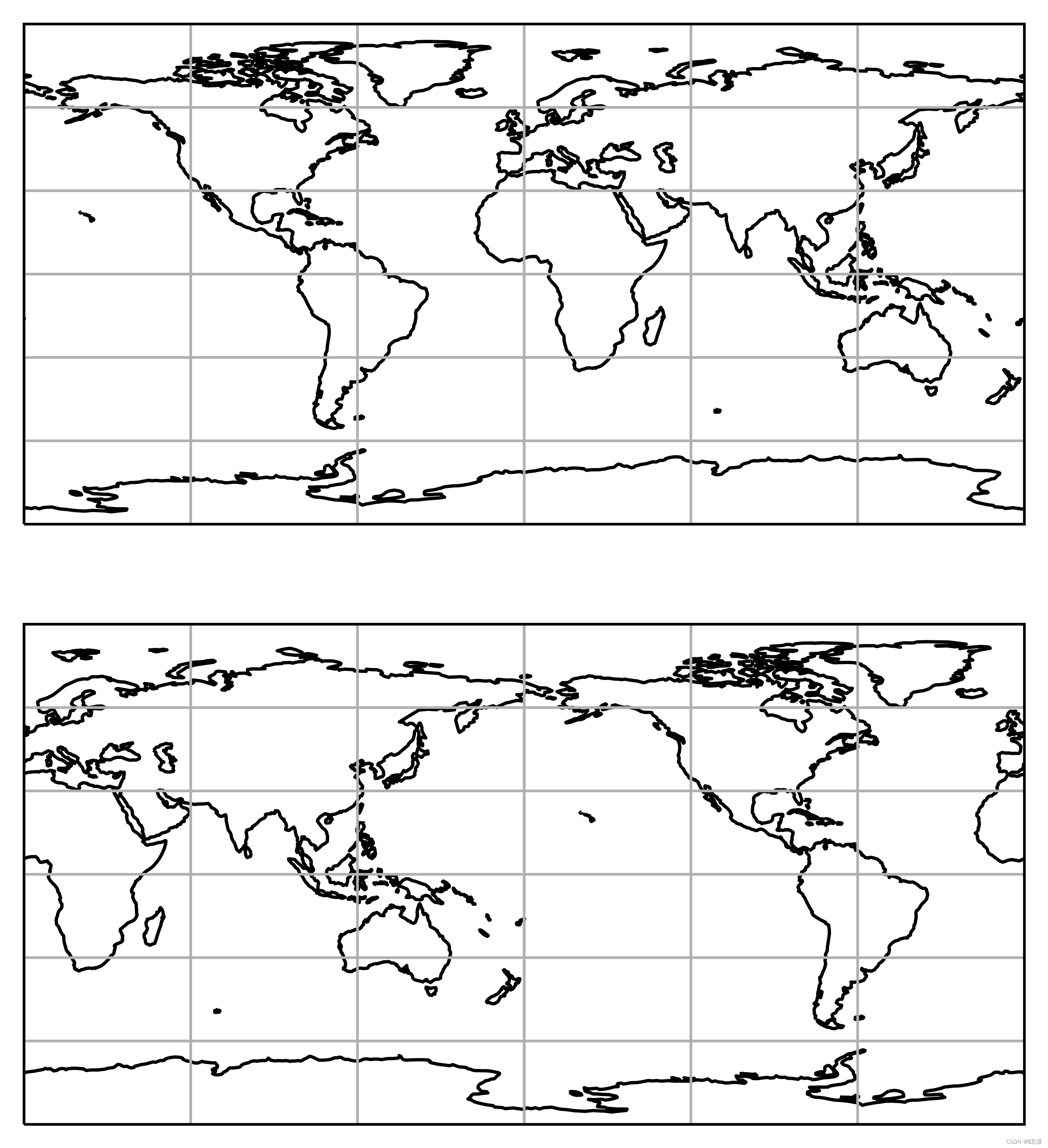
一、PlateCarree（圆柱投影）

PlateCarree 是Cartopy的默认投影，投影将地物投影到圆柱面上再展开，常用来绘制世界地图。该投影具有经线或纬线方向等度数的特点，亦称等经纬度投影。

class cartopy.crs.PlateCarree(central_longitude=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

nplots = 2

fig = plt.figure(figsize=(6, 6))

for i in range(0, nplots):
    central_longitude = 0 if i == 0 else 180
    ax = fig.add_subplot(
        nplots, 1, i+1,
        projection=ccrs.PlateCarree(central_longitude=central_longitude))
    ax.coastlines(resolution='110m')
    ax.gridlines()
plt.show()

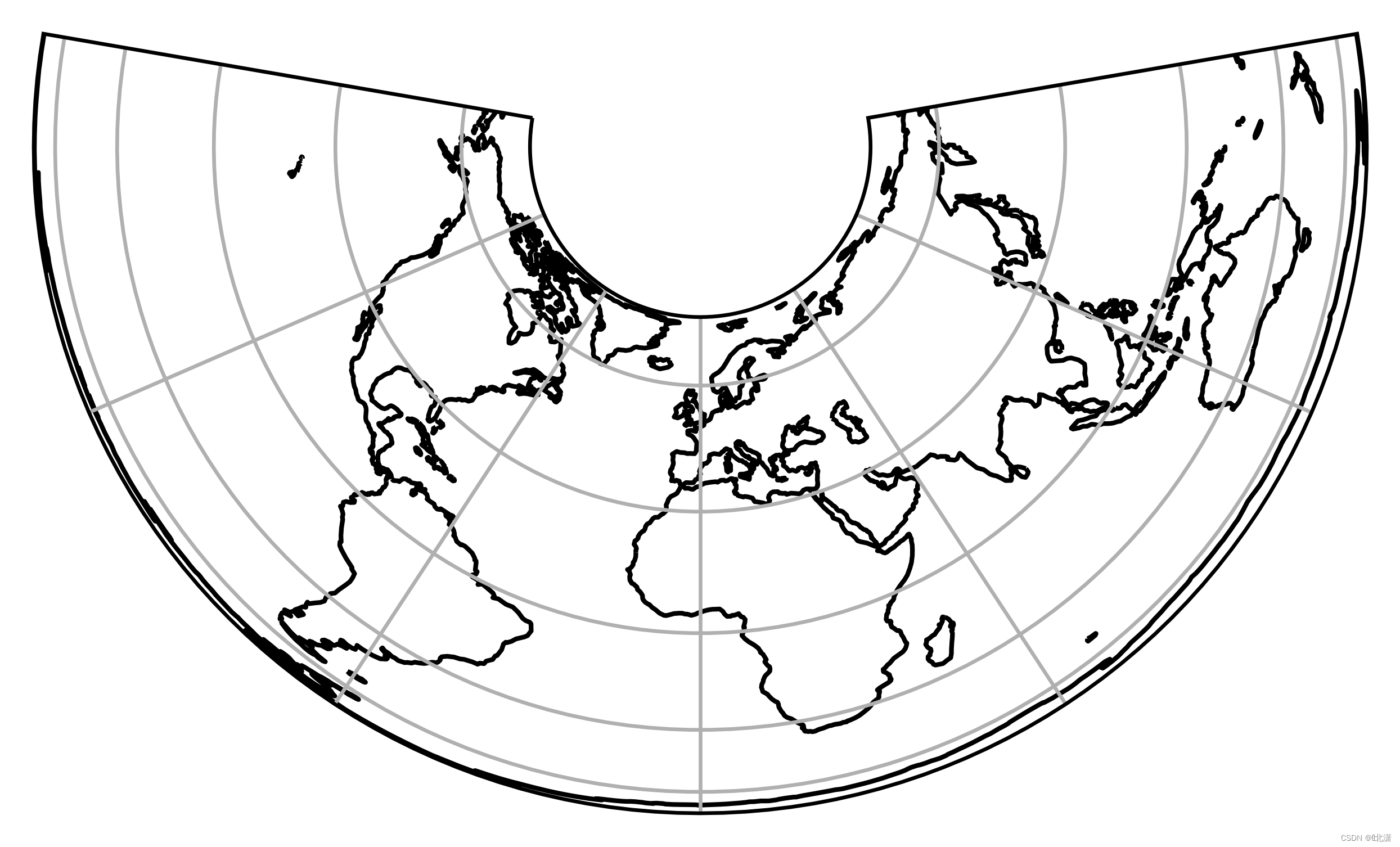
二、AlbersEqualArea（阿尔伯斯等面积投影）

又名“正轴等积割圆锥投影”、“双标准纬线等积圆锥投影”。圆锥投影的一种，为阿尔伯斯（Albers）拟定。纬线为同心圆弧，经线为圆的半径，经线夹角与相应的经差成正比。两条割纬线投影后无任何变形。投影区域面积保持与实地相等。

class cartopy.crs.AlbersEqualArea(central_longitude=0.0, central_latitude=0.0, false_easting=0.0, false_northing=0.0, standard_parallels=(20.0, 50.0), globe=None)[source]

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(5.1299, 3))
ax = plt.axes(projection=ccrs.AlbersEqualArea())
ax.coastlines(resolution='110m')
ax.gridlines()

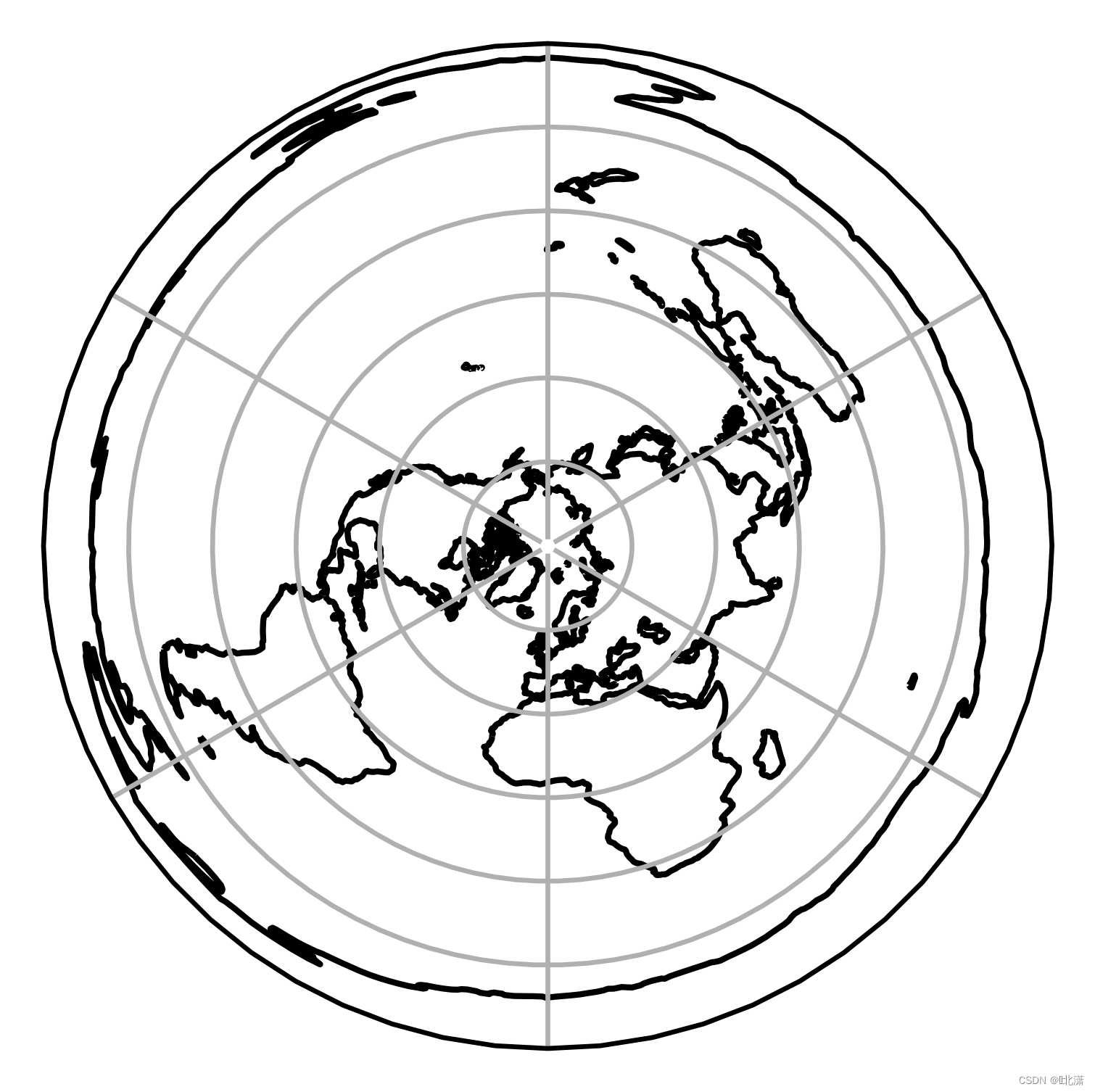
三、AzimuthalEquidistant（等距方位角投影）

等距方位投影是指使图上面积和相应的实际地面面积相等的方位投影，分为正轴，横轴、斜轴投影。其中纬线为同心圆弧，经线为圆的半径。该投影提供了围绕中心位置的精确角度和距离。其他角度、距离或区域可能会变形。

class cartopy.crs.AzimuthalEquidistant(central_longitude=0.0, central_latitude=0.0, false_easting=0.0, false_northing=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.AzimuthalEquidistant(central_latitude=90))
ax.coastlines(resolution='110m')
ax.gridlines()

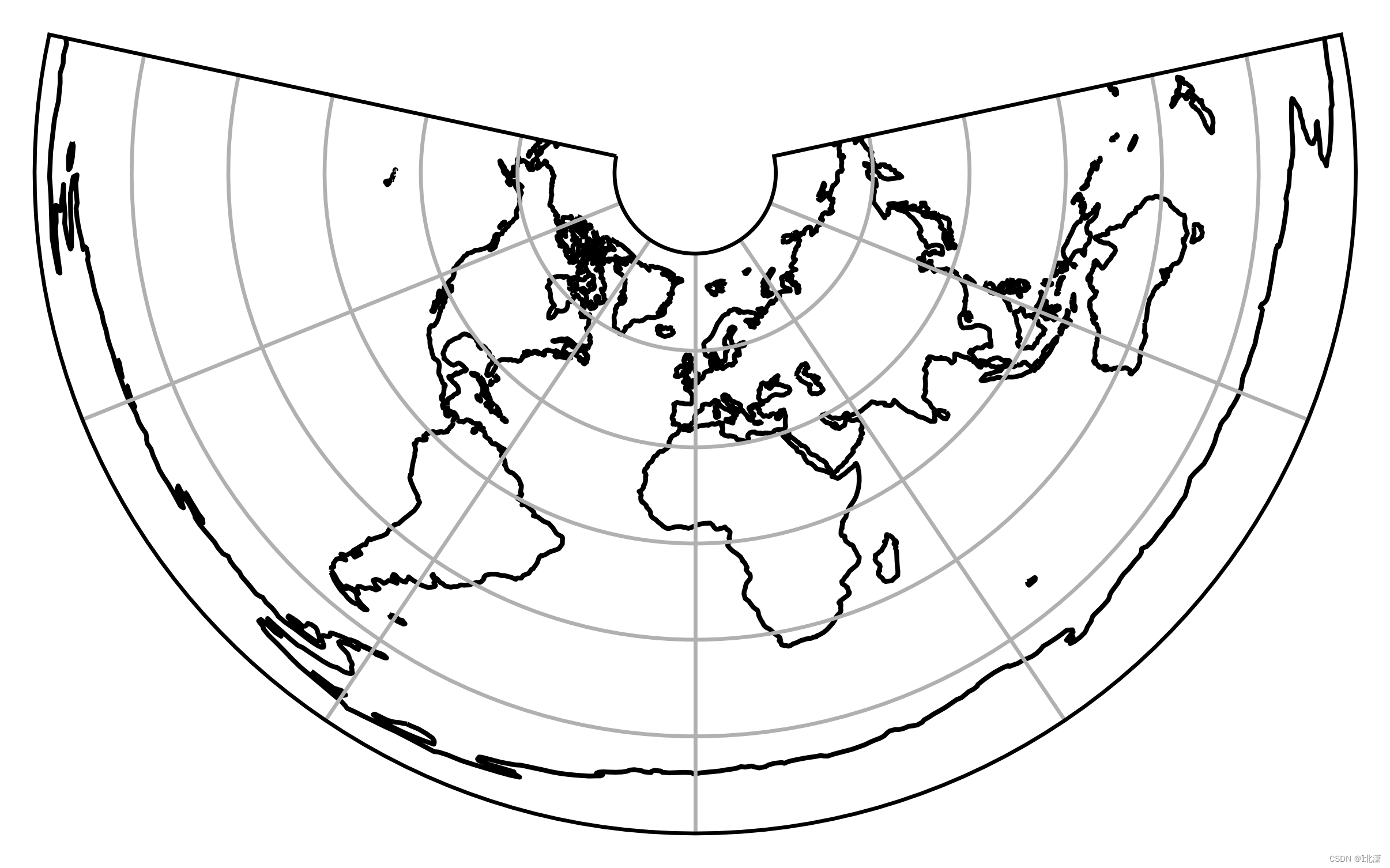
四、EquidistantConic（等距圆锥投影）

等距圆锥投影指沿经线方向长度没有变形的圆锥投影。在这种图上，纬线间距相等，沿经线方向长度没有变形。除经线方向外其它方向的长度都有变形，面积和角度也变形，但变形都不太大。这种投影适于编制各种教学用图和交通图。但在我国使用比较少。在中学使用的世界地图册中的苏联图是采用这种投影。

class cartopy.crs.EquidistantConic(central_longitude=0.0, central_latitude=0.0, false_easting=0.0, false_northing=0.0, standard_parallels=(20.0, 50.0), globe=None)[source]

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(4.9603, 3))
ax = plt.axes(projection=ccrs.EquidistantConic())
ax.coastlines(resolution='110m')
ax.gridlines()

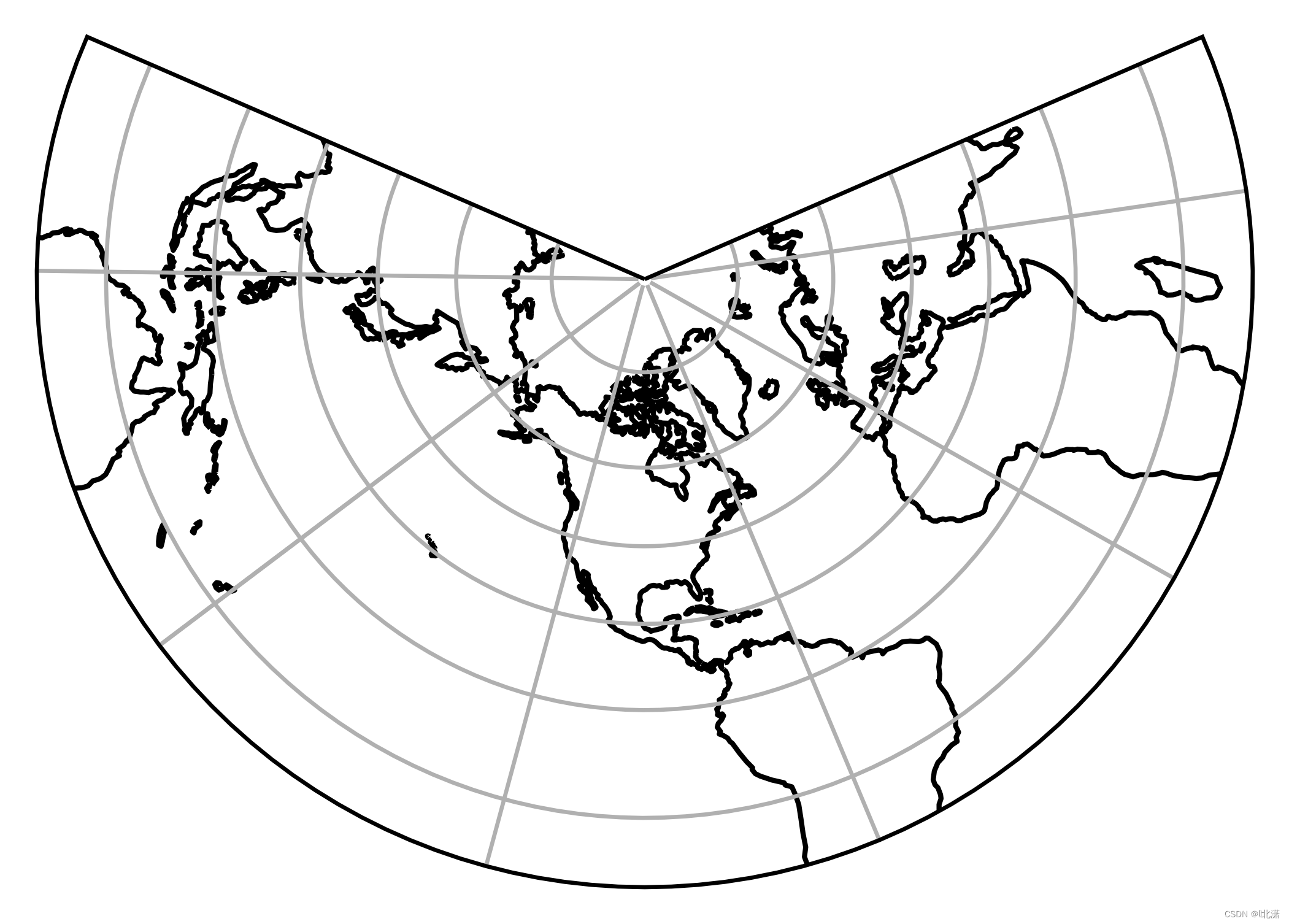
五、LambertConformal（兰伯特等角圆锥投影）

兰勃特投影是由德国数学家兰勃特（J.H.Lambert）拟定的正形圆锥投影。等角圆锥投影。设想用一个正圆锥切于或割于球面，应用等角条件将地球面投影到圆锥面上，然后沿一母线展开成平面。投影后纬线为同心圆圆弧，经线为同心圆半径。没有角度变形，经线长度比和纬线长度比相等。适于制作沿纬线分布的中纬度地区中、小比例尺地图。国际上用此投影编制1∶100万地形图和航空图；

class cartopy.crs.LambertConformal(central_longitude=-96.0, central_latitude=39.0, false_easting=0.0, false_northing=0.0, standard_parallels=(33, 45), globe=None, cutoff=-30)[source]

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(4.2897, 3))
ax = plt.axes(projection=ccrs.LambertConformal())
ax.coastlines(resolution='110m')
ax.gridlines()

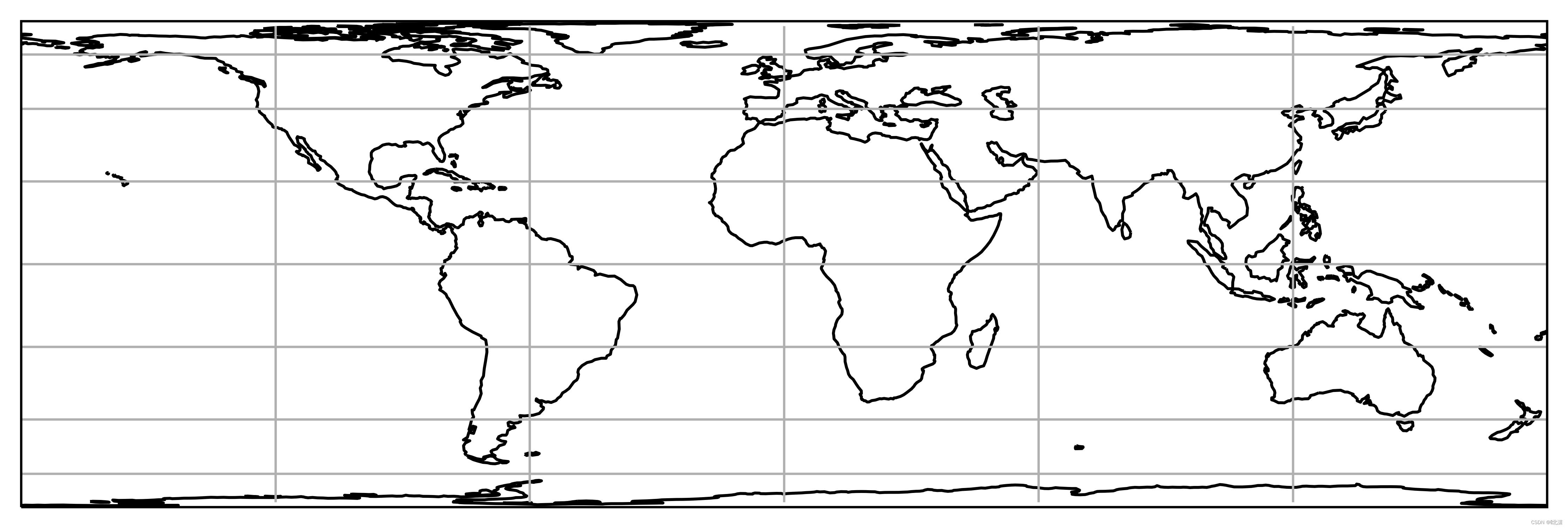
六、LambertCylindrical（兰伯特圆柱投影）

兰伯特圆锥投影的特例，当圆锥顶角为0°，经线成为平行直线，这就成为圆柱投影了，具有等积的特点。

class cartopy.crs.LambertCylindrical(central_longitude=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(9.4248, 3))
ax = plt.axes(projection=ccrs.LambertCylindrical())
ax.coastlines(resolution='110m')
ax.gridlines()

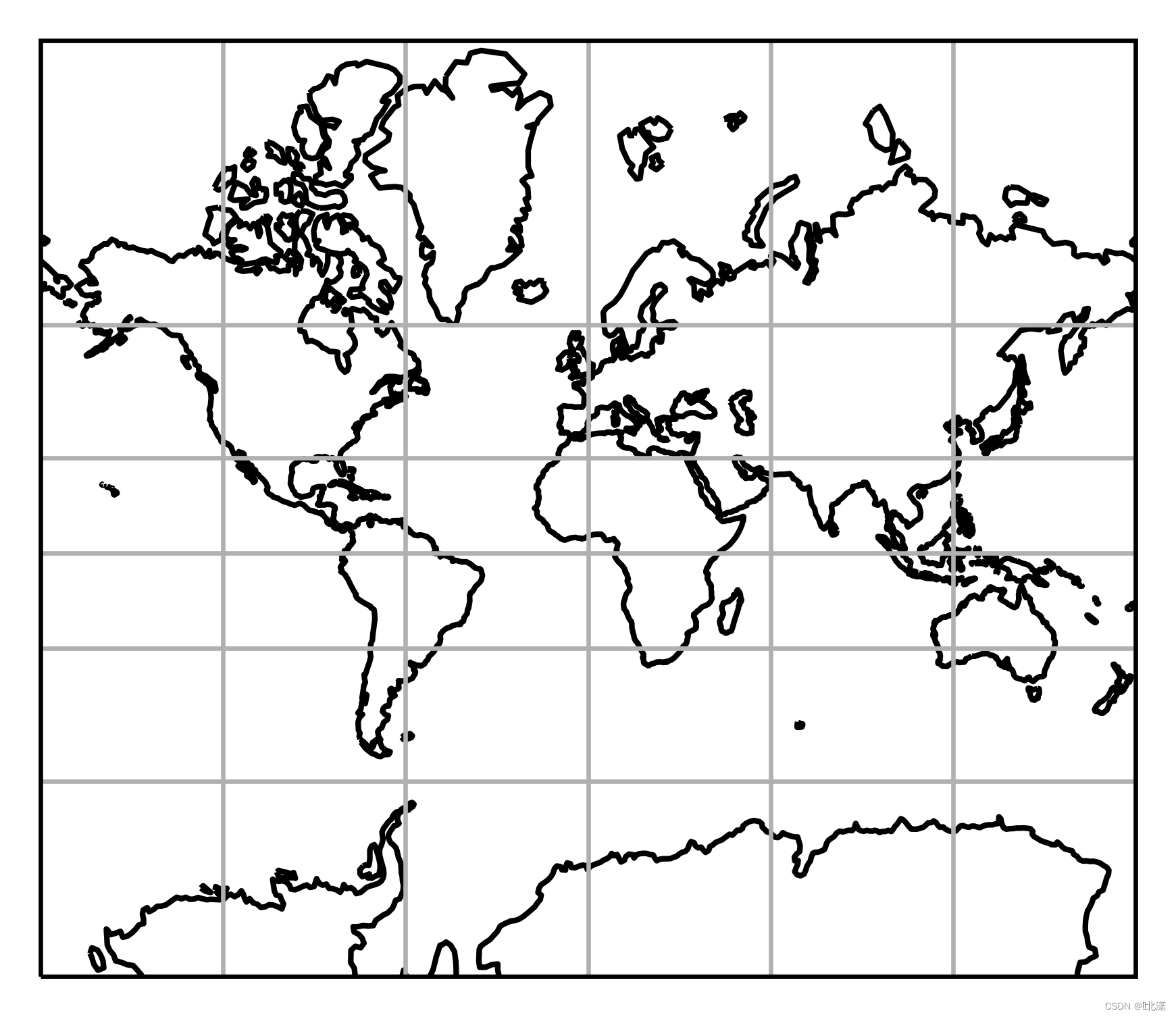
七、Mercator（墨卡托投影）

墨卡托投影，是正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球，按等角条件，将经纬网投影到圆柱面上，将圆柱面展为平面后，即得本投影。墨卡托投影在切圆柱投影与割圆柱投影中，最早也是最常用的是切圆柱投影。

class cartopy.crs.Mercator(central_longitude=0.0, min_latitude=-80.0, max_latitude=84.0, globe=None, latitude_true_scale=None, false_easting=0.0, false_northing=0.0, scale_factor=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3.5091, 3))
ax = plt.axes(projection=ccrs.Mercator())
ax.coastlines(resolution='110m')
ax.gridlines()

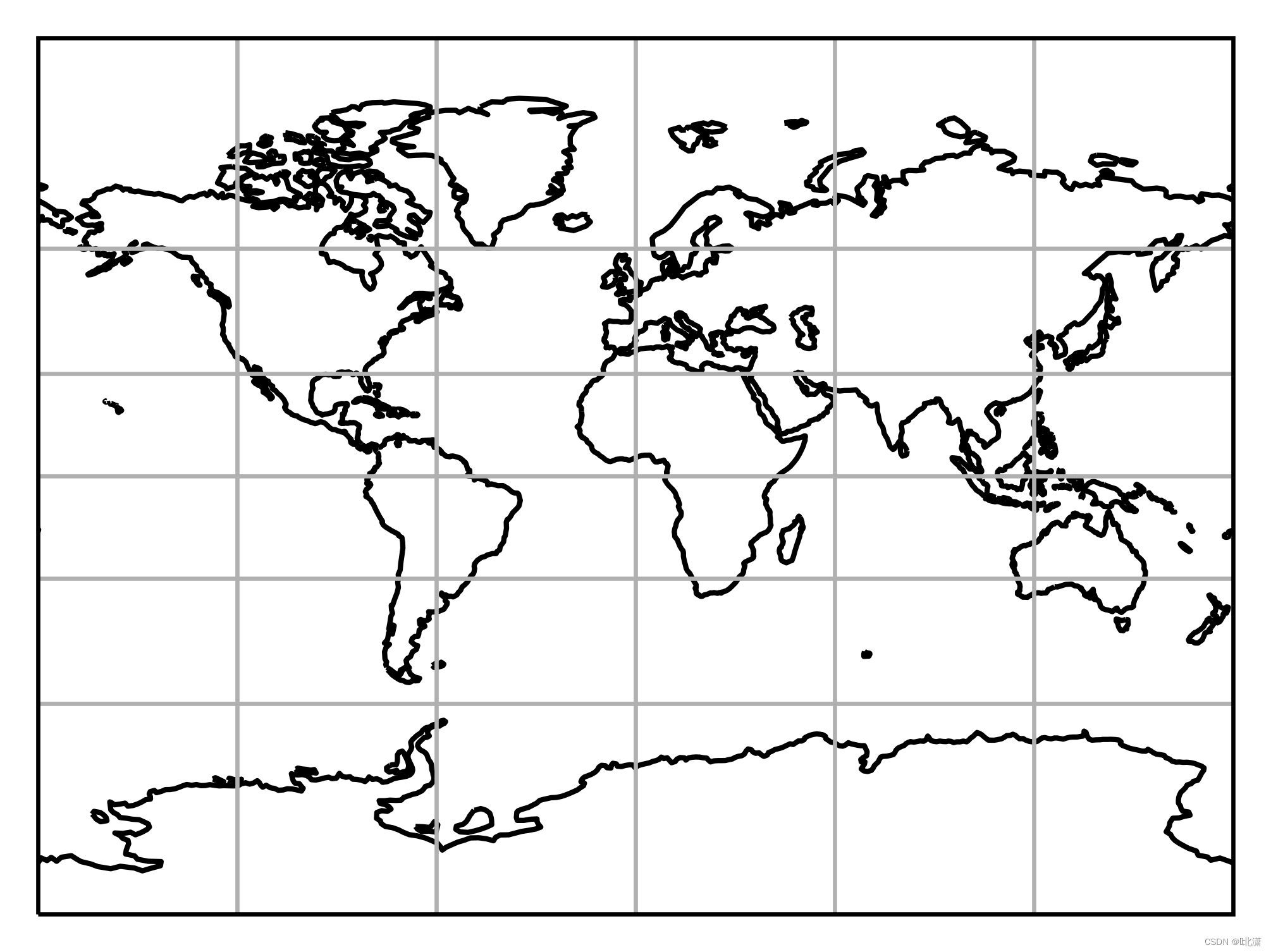
八、Miller（米勒投影）

米勒圆柱投影是一种折衷圆柱地图投影。该投影是墨卡托投影的改良型投影，因此，二者在赤道附近几乎相同。虽然米勒投影不会将极点投影到无穷大，但是极点处的畸变仍然非常严重。

class cartopy.crs.Miller(central_longitude=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(4.0917, 3))
ax = plt.axes(projection=ccrs.Miller())
ax.coastlines(resolution='110m')
ax.gridlines()

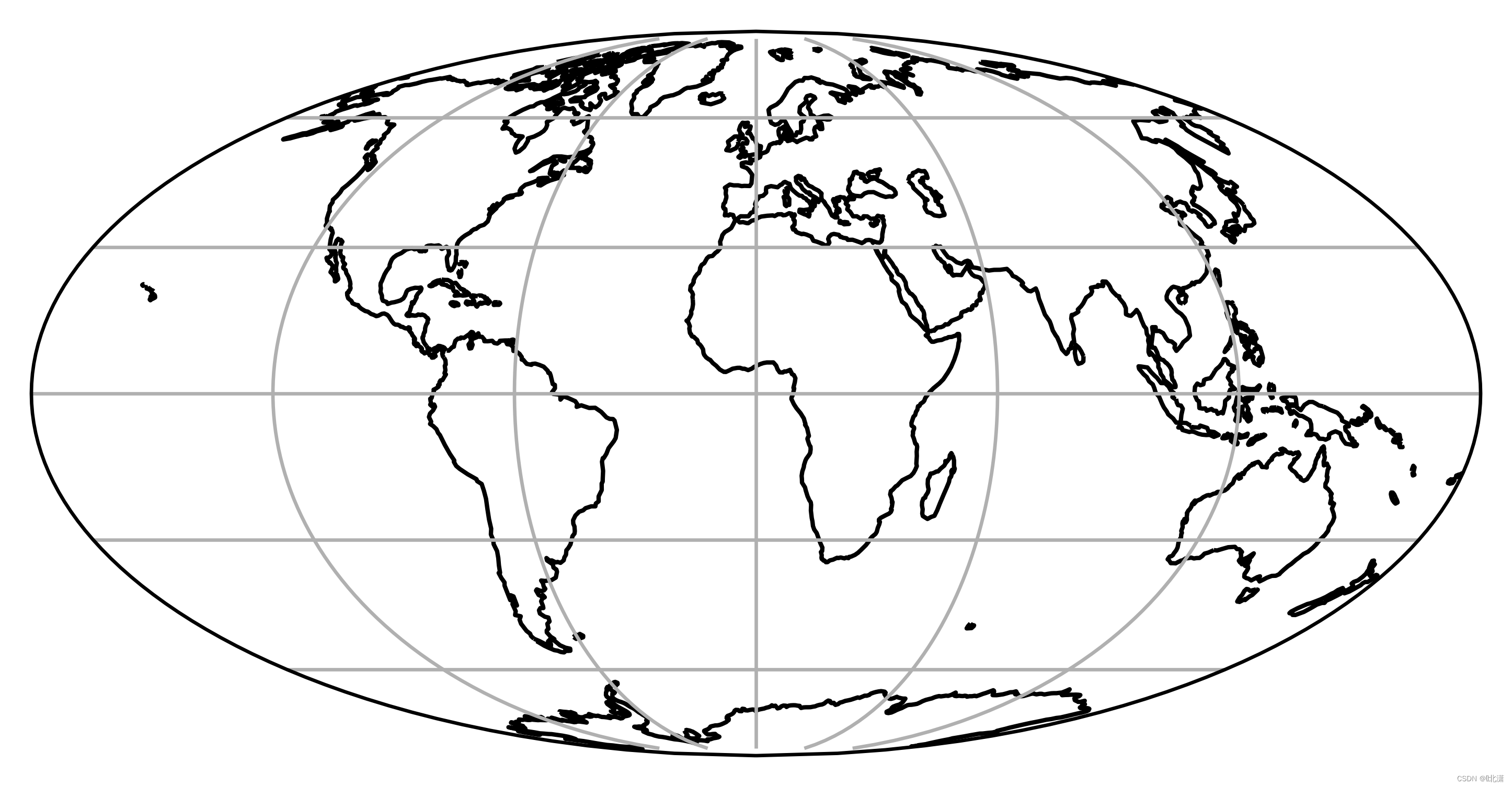
九、Mollweide（摩尔威德投影）

摩尔威德投影（Mollweide Projection）是经线投影成为椭圆曲线的一种等面积伪圆柱投影。这一投影是德国数学家摩尔威德（K.B.Mollweide 1774~1825年）于1805年创立的米勒圆柱投影是一种折衷圆柱地图投影。

class cartopy.crs.Mollweide(central_longitude=0, globe=None, false_easting=None, false_northing=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.Mollweide())
ax.coastlines(resolution='110m')
ax.gridlines()

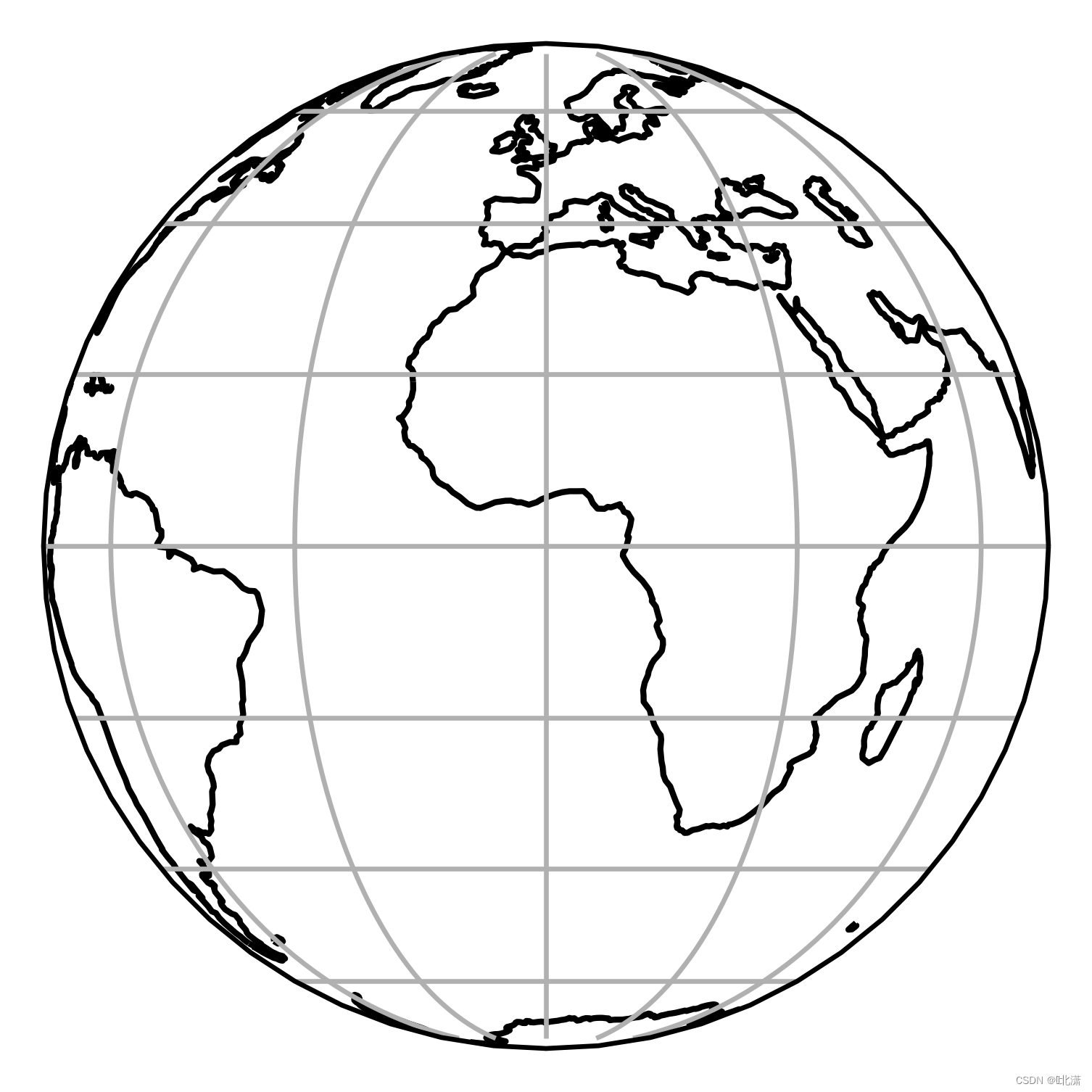
十、Orthographic（正射投影）

正射投影又称“直角投影”。属任意性质的透视方位投影。

class cartopy.crs.Orthographic(central_longitude=0.0, central_latitude=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.Orthographic())
ax.coastlines(resolution='110m')
ax.gridlines()

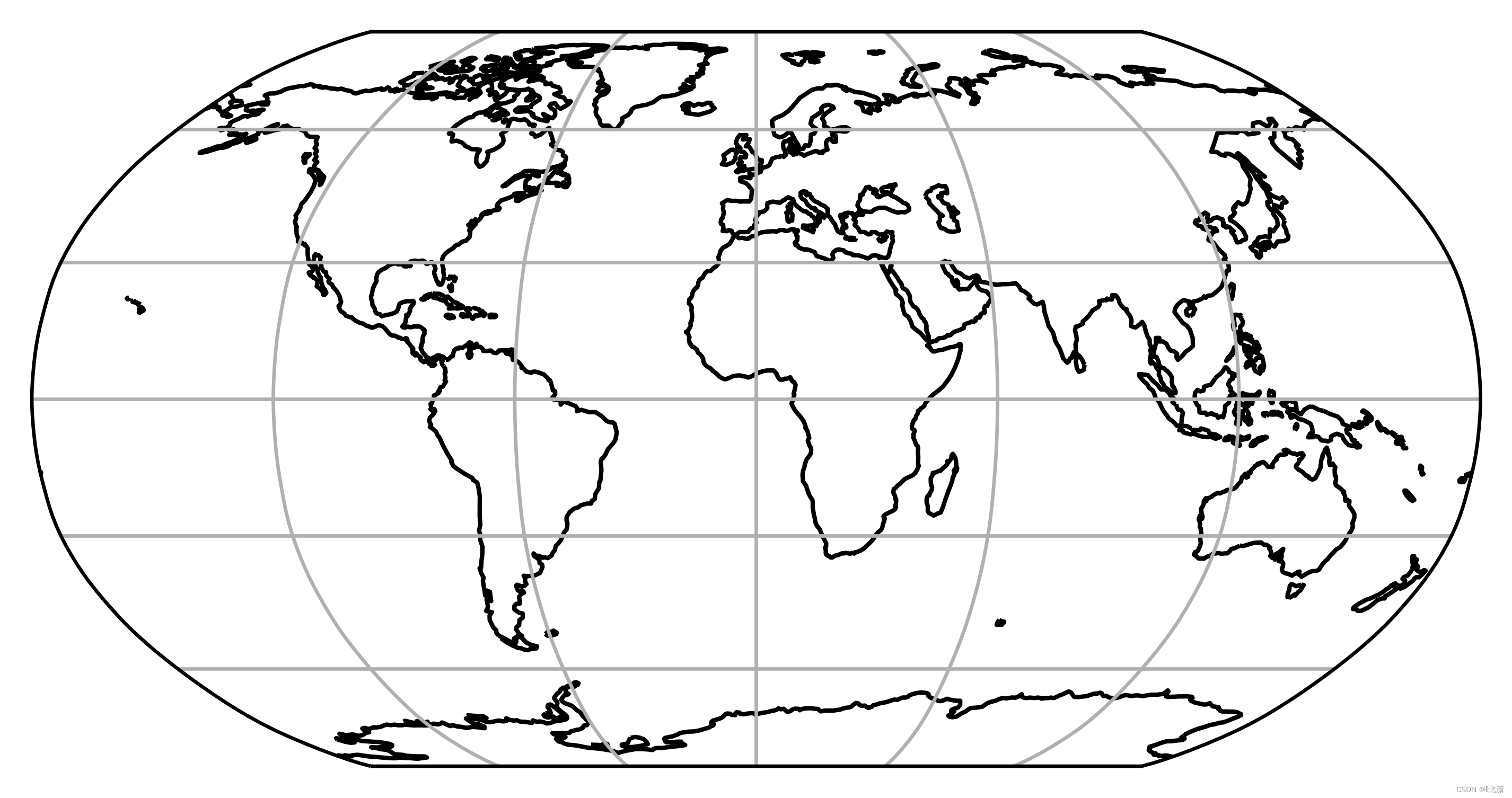
十一、Robinson（罗宾森投影）

伪圆柱投影。类似于椭圆弧的经线等间距分布，并且以中央子午线为中心向两侧凸出。中央子午线是一条直线，其长度为赤道的 0.51 倍。纬线是直线，在南北纬 38° 之间等间距分布，在此范围外的间距减小。极点的投影是长度为赤道 0.53 倍的直线。该投影基于图表坐标，而不是数学公式。

class cartopy.crs.Robinson(central_longitude=0, globe=None, false_easting=None, false_northing=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(5.915, 3))
ax = plt.axes(projection=ccrs.Robinson())
ax.coastlines(resolution='110m')
ax.gridlines()

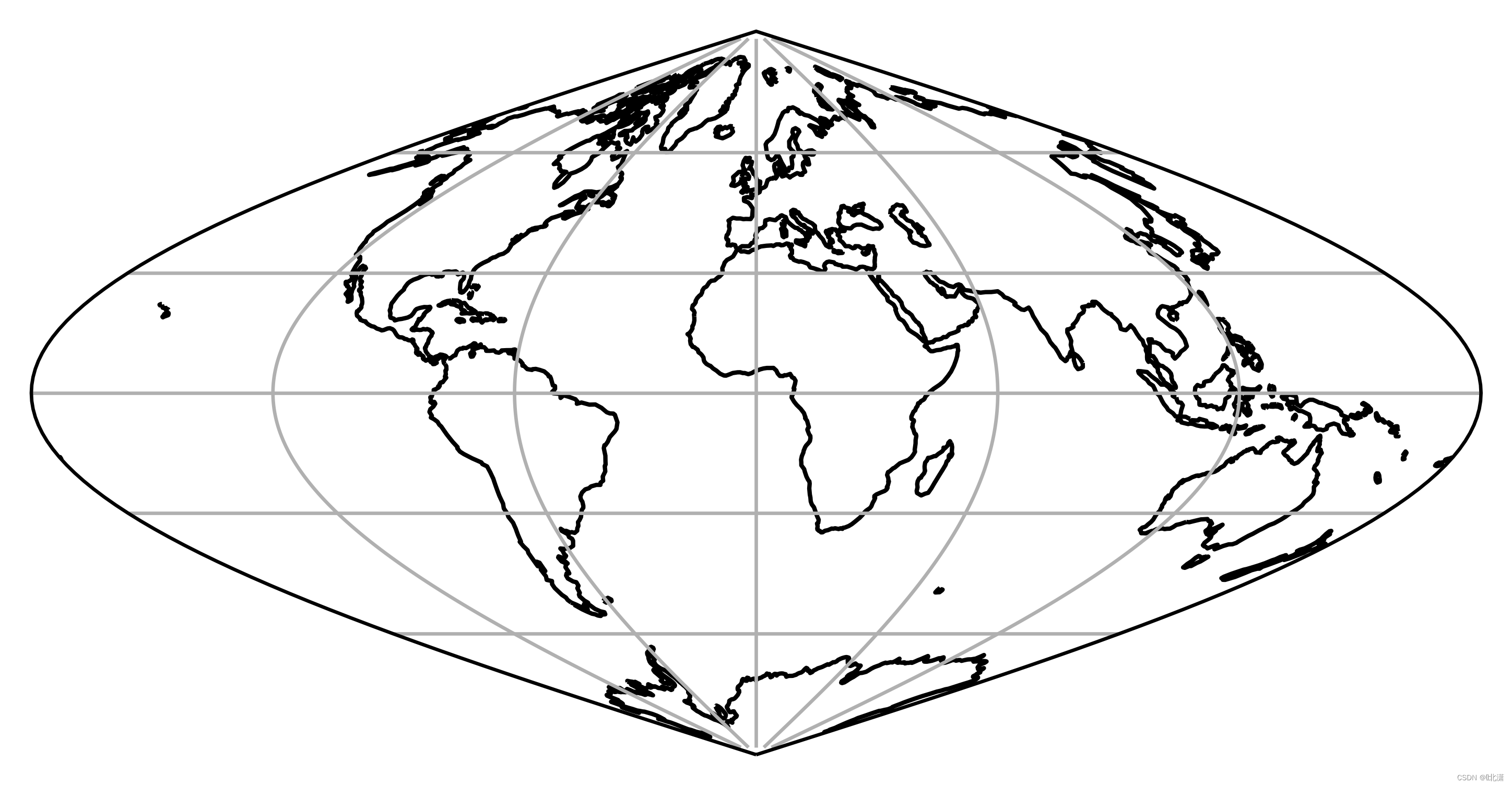
十二、Sinusoidal（正弦投影）

该投影也称为桑逊-弗兰斯蒂德地图投影，用于世界地图时，无论是否存在等角变形，它都能保持等积。其替代形式通过中断海洋投影的连续性，并使各大陆在各自中央子午线附近居中，来减小外侧子午线方向上的变形程度，反之亦然。

class cartopy.crs.Sinusoidal(central_longitude=0.0, false_easting=0.0, false_northing=0.0, globe=None)[source]

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6.0101, 3))
ax = plt.axes(projection=ccrs.Sinusoidal())
ax.coastlines(resolution='110m')
ax.gridlines()

十三、Stereographic（极射赤面投影）

又称平射投影、等角方位投影、球面投影等，透视方位投影的一种。视点位于地球球体表面，投影平面位于视点正对面。球面投影的投影特性为：地面上的圆投影后仍为一个圆，经纬线为相互正交的圆弧线。适于制作圆形区域的小比例尺地图。

class cartopy.crs.Stereographic(central_latitude=0.0, central_longitude=0.0, false_easting=0.0, false_northing=0.0, true_scale_latitude=None, scale_factor=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.Stereographic())
ax.coastlines(resolution='110m')
ax.gridlines()

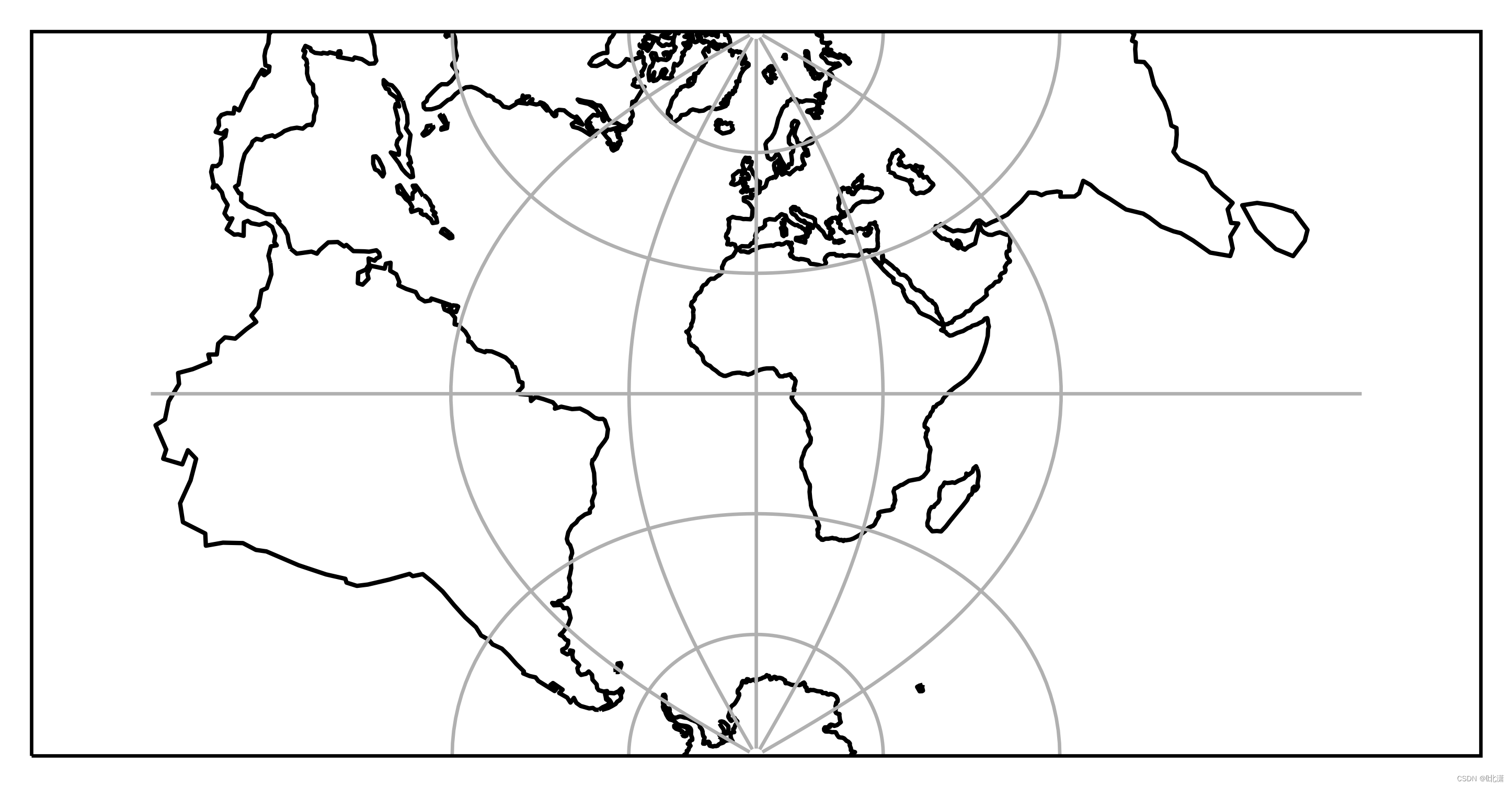
十四、TransverseMercator（横轴墨卡托投影）

墨卡托投影，是正轴等角圆柱投影。由荷兰地图学家墨卡托(G.Mercator)于1569年创立。假想一个与地轴方向一致的圆柱切或割于地球，按等角条件，将经纬网投影到圆柱面上，将圆柱面展为平面后，即得本投影。投影面的轴（圆锥圆柱的轴线，平面的法线）与地球赤道面重合。

class cartopy.crs.TransverseMercator(central_longitude=0.0, central_latitude=0.0, false_easting=0.0, false_northing=0.0, scale_factor=1.0, globe=None, approx=False)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.TransverseMercator(approx=False))
ax.coastlines(resolution='110m')
ax.gridlines()

十五、UTM（通用横轴墨卡托投影）

通用墨卡尔投影是英、美、日、加拿大等国地形图最通用的投影。简称“UTM投影”。属等角横轴割圆柱投影。因投影圆柱与地球相割，中央经线投影后的长度比为0.9996，投影带各部分的长度变形比较平稳，其6°带内长度变形小于0.1%。

class cartopy.crs.UTM(zone, southern_hemisphere=False, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

nplots = 60

fig = plt.figure(figsize=(10, 3))

for i in range(0, nplots):
    ax = fig.add_subplot(1, nplots, i+1, projection=ccrs.UTM(zone=i+1, southern_hemisphere=True))
    ax.coastlines(resolution='110m')
    ax.gridlines()

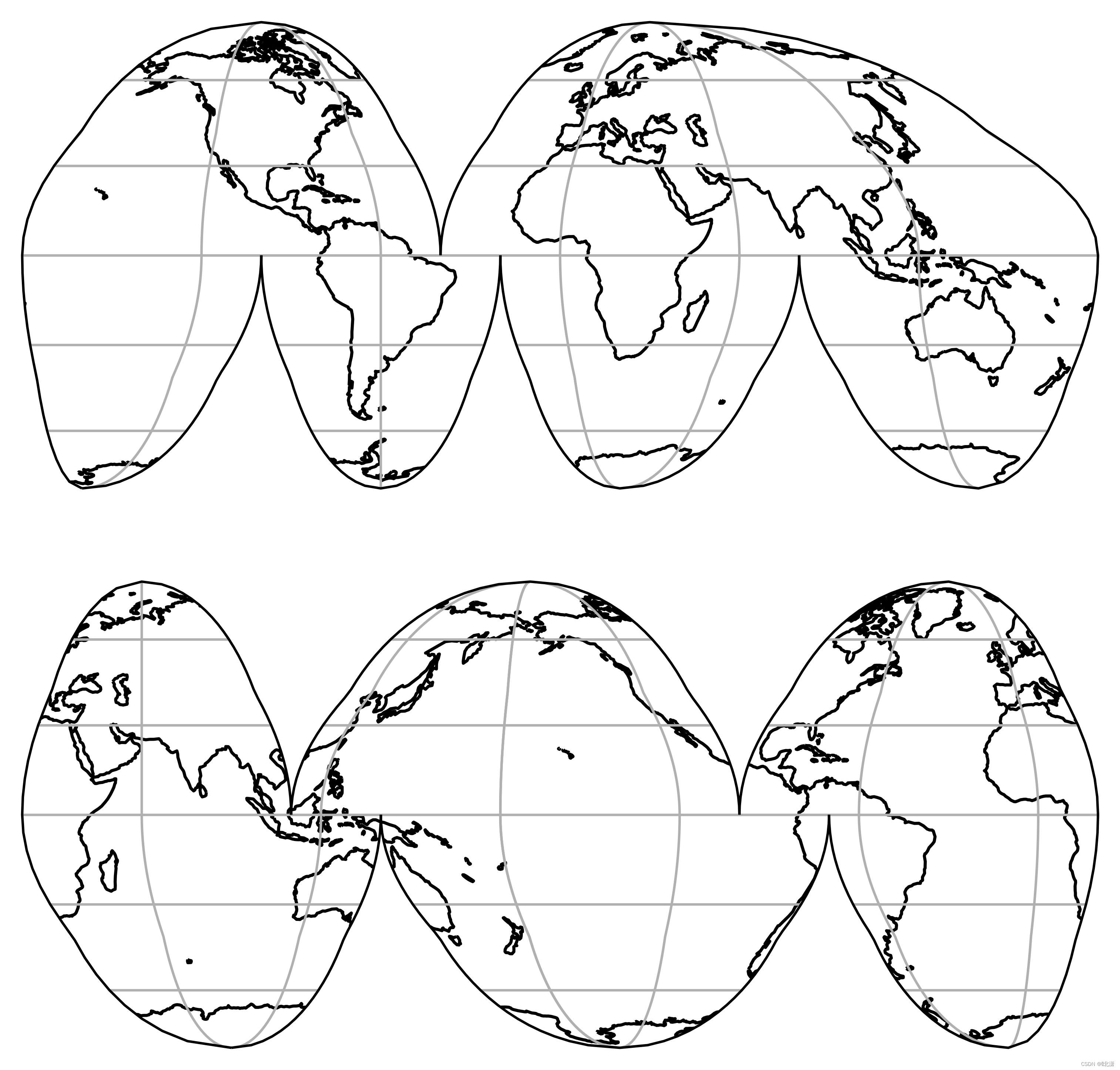
十六、InterruptedGoodeHomolosine（分瓣正弦古德投影）

古德分瓣投影又称“古德投影”、“古德分瓣法”。美国地理学家古德于1923年提出，故名。一种用分瓣法表示的等积伪圆柱投影。

class cartopy.crs.InterruptedGoodeHomolosine(central_longitude=0, globe=None, emphasis='land')

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

fig = plt.figure(figsize=(6.9228, 6))

ax1 = fig.add_subplot(2, 1, 1, projection=ccrs.InterruptedGoodeHomolosine(emphasis='land'))
ax1.coastlines(resolution='110m')
ax1.gridlines()

ax2 = fig.add_subplot(2, 1, 2, projection=ccrs.InterruptedGoodeHomolosine(central_longitude=-160, emphasis='ocean'))
ax2.coastlines(resolution='110m')
ax2.gridlines()

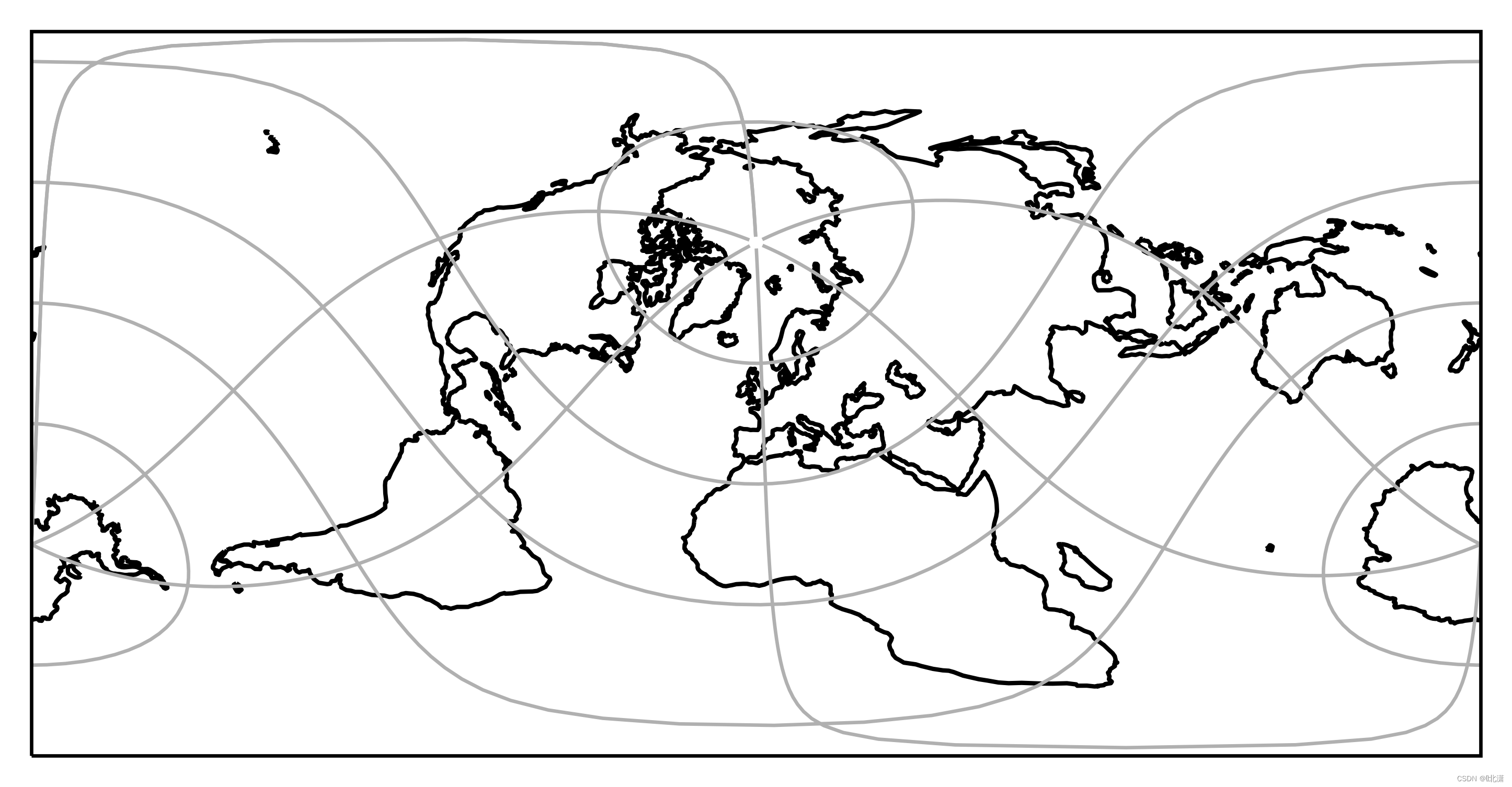
十七、RotatedPole（旋转极投影）

旋转极投影，属于极投影的变体，常被用于天气预测模型中。

class cartopy.crs.RotatedPole(pole_longitude=0.0, pole_latitude=90.0, central_rotated_longitude=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.RotatedPole(pole_latitude=37.5, pole_longitude=177.5))
ax.coastlines(resolution='110m')
ax.gridlines()

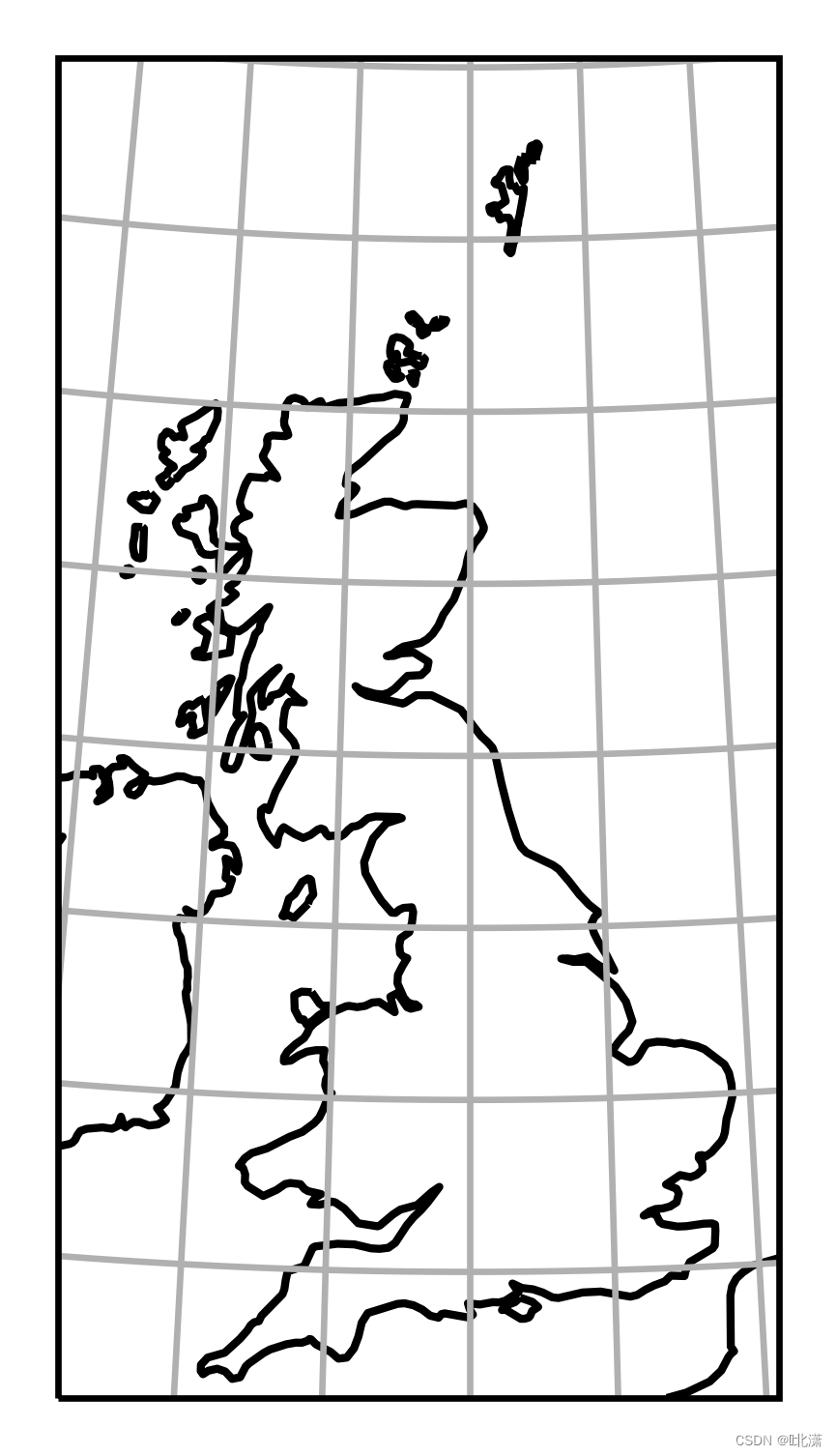
十八、OSGB（倾斜投影）

这是一种投影于 Airy 旋转椭球体之上的横轴墨卡托投影。原点为 49° N 和 2° W。中央子午线的比例为 0.9996012717。如果两个数据集具有不同的比例尺因子值，它们将被视为不同的数据集。用于英国军用测量。

class cartopy.crs.OSGB(approx=False)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(1.6154, 3))
ax = plt.axes(projection=ccrs.OSGB(approx=False))
ax.coastlines(resolution='50m')
ax.gridlines()

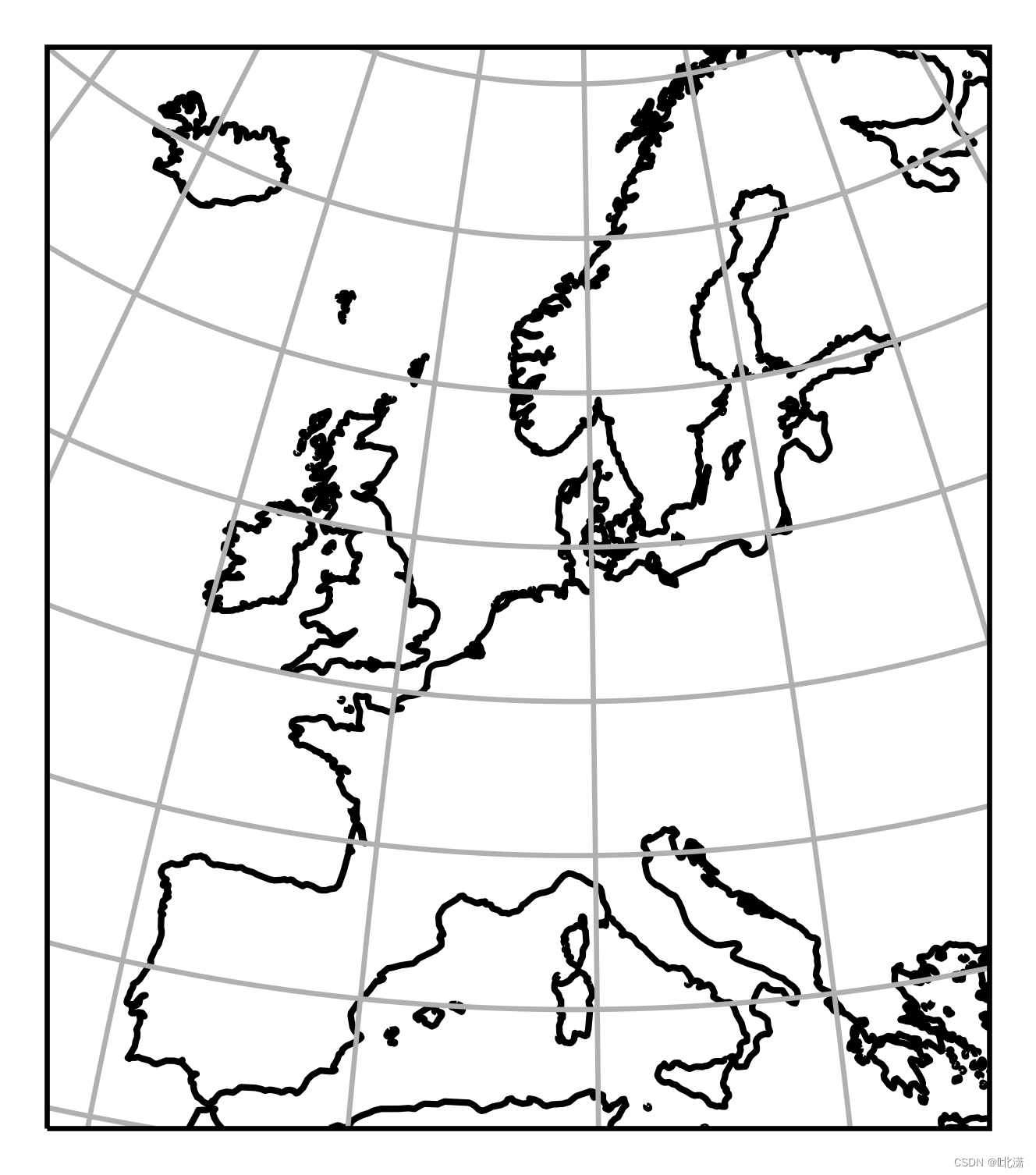
十九、EuroPP（欧洲投影）

用于绘制欧洲地图的一种等距圆锥投影。

class cartopy.crs.EuroPP

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(2.6154, 3))
ax = plt.axes(projection=ccrs.EuroPP())
ax.coastlines(resolution='50m')
ax.gridlines()

二十、Geostationary（对地静止投影）

（地球同步卫星）视角，视点在赤道上空某一点处。这种投影好像在地球同步（GEO）卫星上观察到的地球。

class cartopy.crs.Geostationary(central_longitude=0.0, satellite_height=35785831, false_easting=0, false_northing=0, globe=None, sweep_axis='y')

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.Geostationary())
ax.coastlines(resolution='110m')
ax.gridlines()

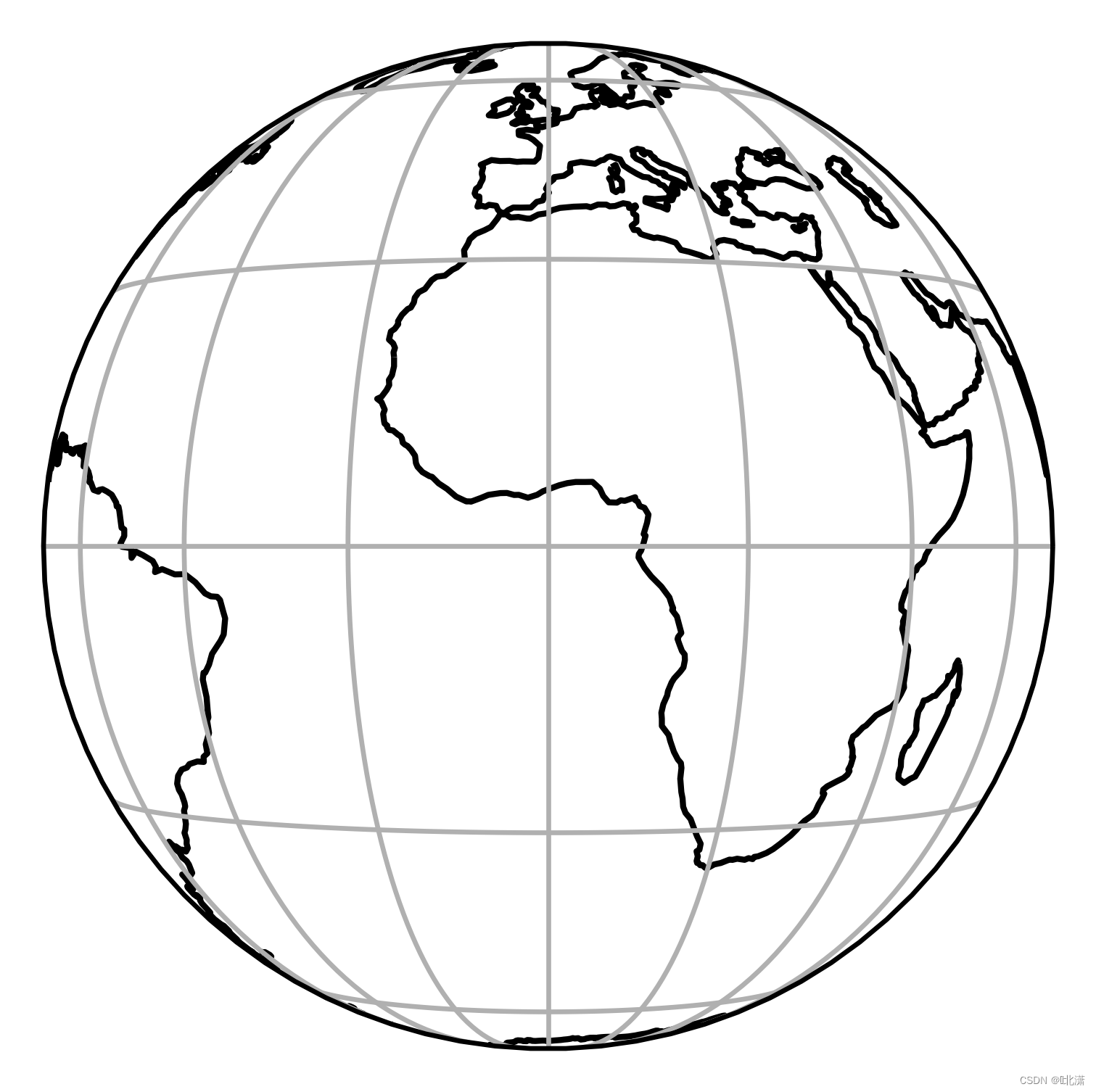
二十一、NearsidePerspective（近侧透视投影）

（驾驶员）视角，视点在地球外某一点处。这种投影好像在高空中某处宇宙飞船驾驶员的视角。

class cartopy.crs.NearsidePerspective(central_longitude=0.0, central_latitude=0.0, satellite_height=35785831, false_easting=0, false_northing=0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.NearsidePerspective(
                        central_latitude=50.72,
                        central_longitude=-3.53,
                        satellite_height=10000000.0))
ax.coastlines(resolution='110m')
ax.gridlines()

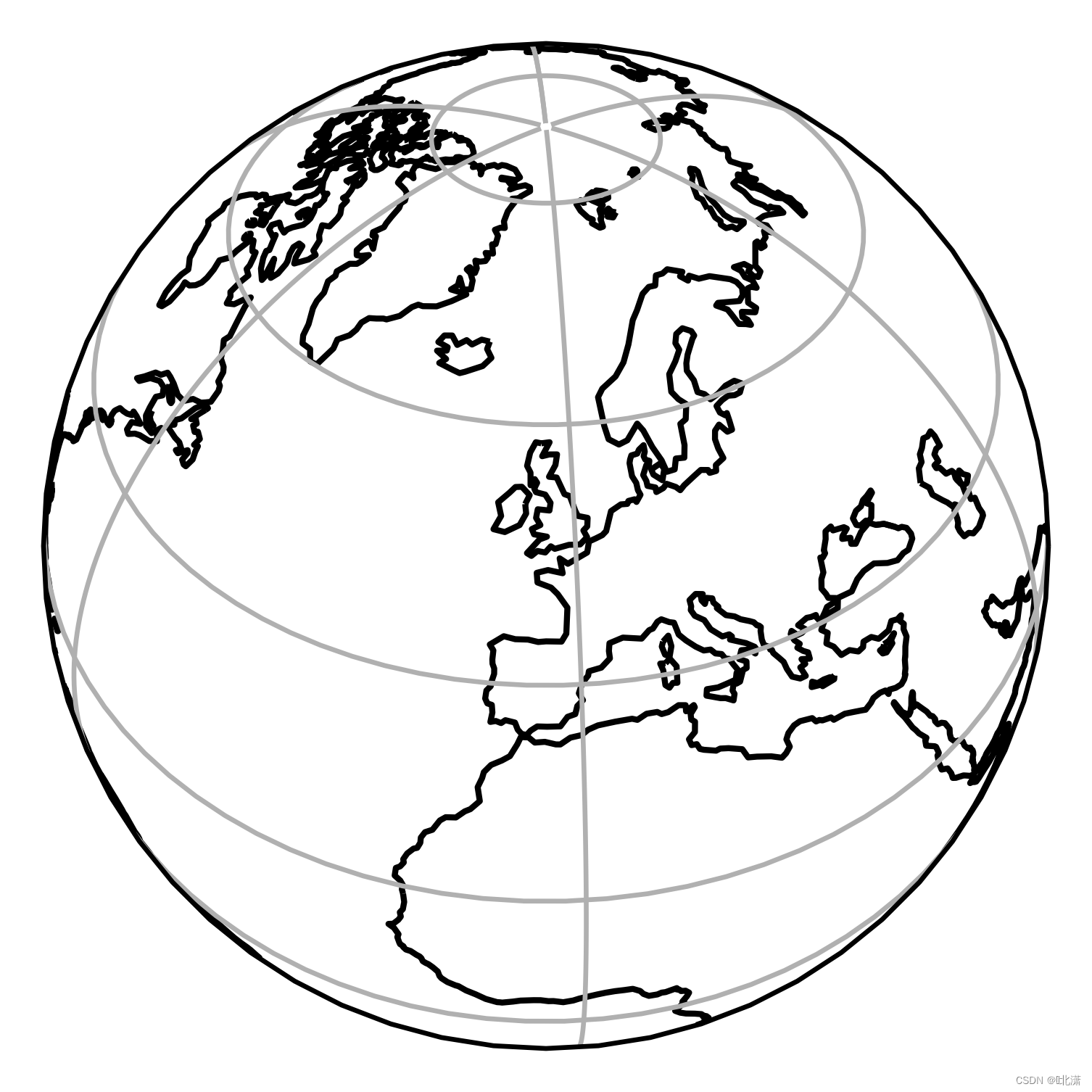
二十二、EckertI（埃克特第一投影）

一种伪圆柱投影，纬线和经线是等间距的直线。极点和中央子午线为直线，其长度是赤道长度的一半。

class cartopy.crs.EckertI(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.EckertI())
ax.coastlines(resolution='110m')
ax.gridlines()

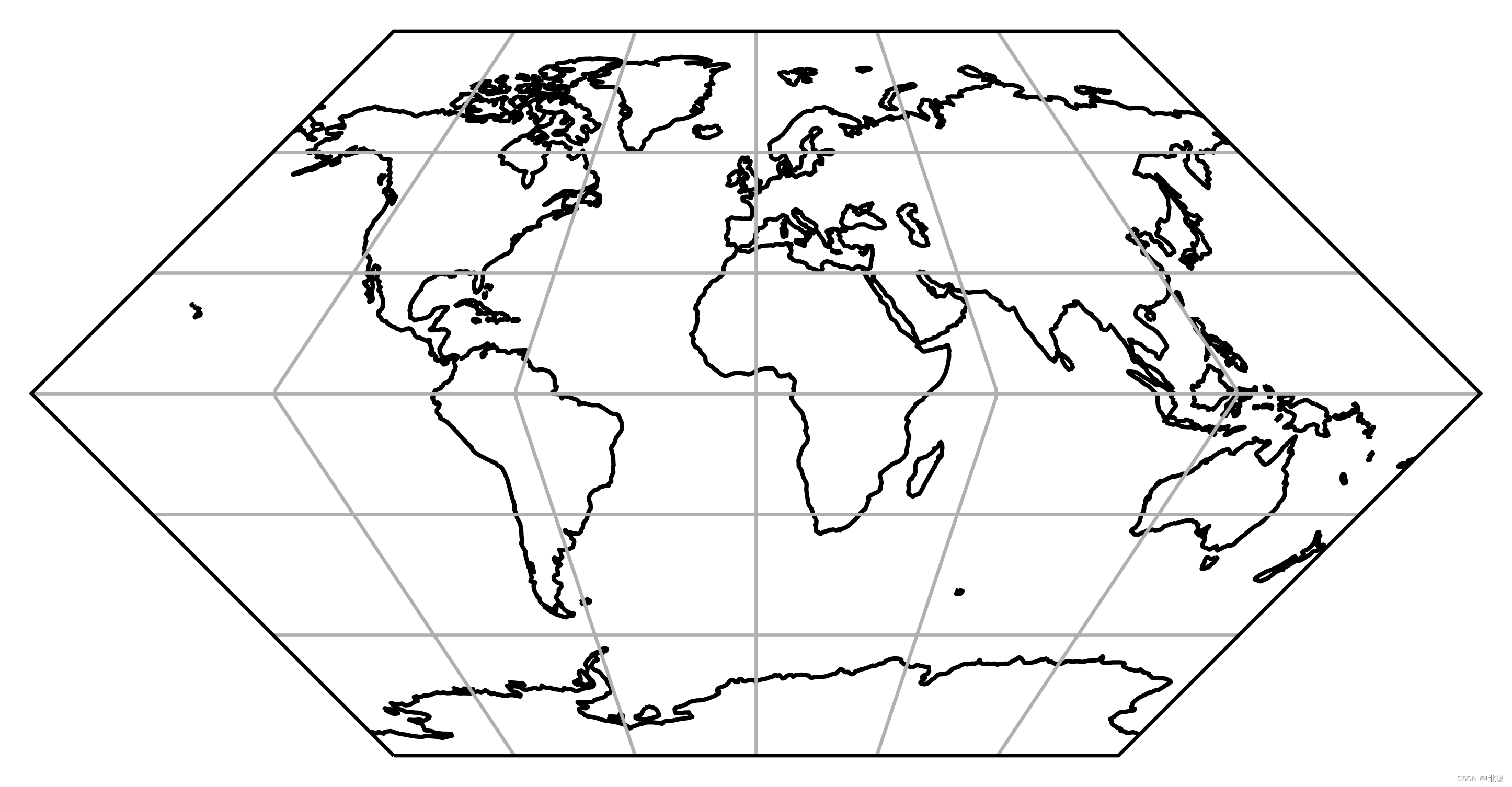
二十三、EckertII（埃克特第二投影）

伪圆柱投影。纬线是非等间距的直线。经线是等间距的直线。极点和中央子午线为直线，其长度是赤道长度的一半。

class cartopy.crs.EckertII(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.EckertII())
ax.coastlines(resolution='110m')
ax.gridlines()

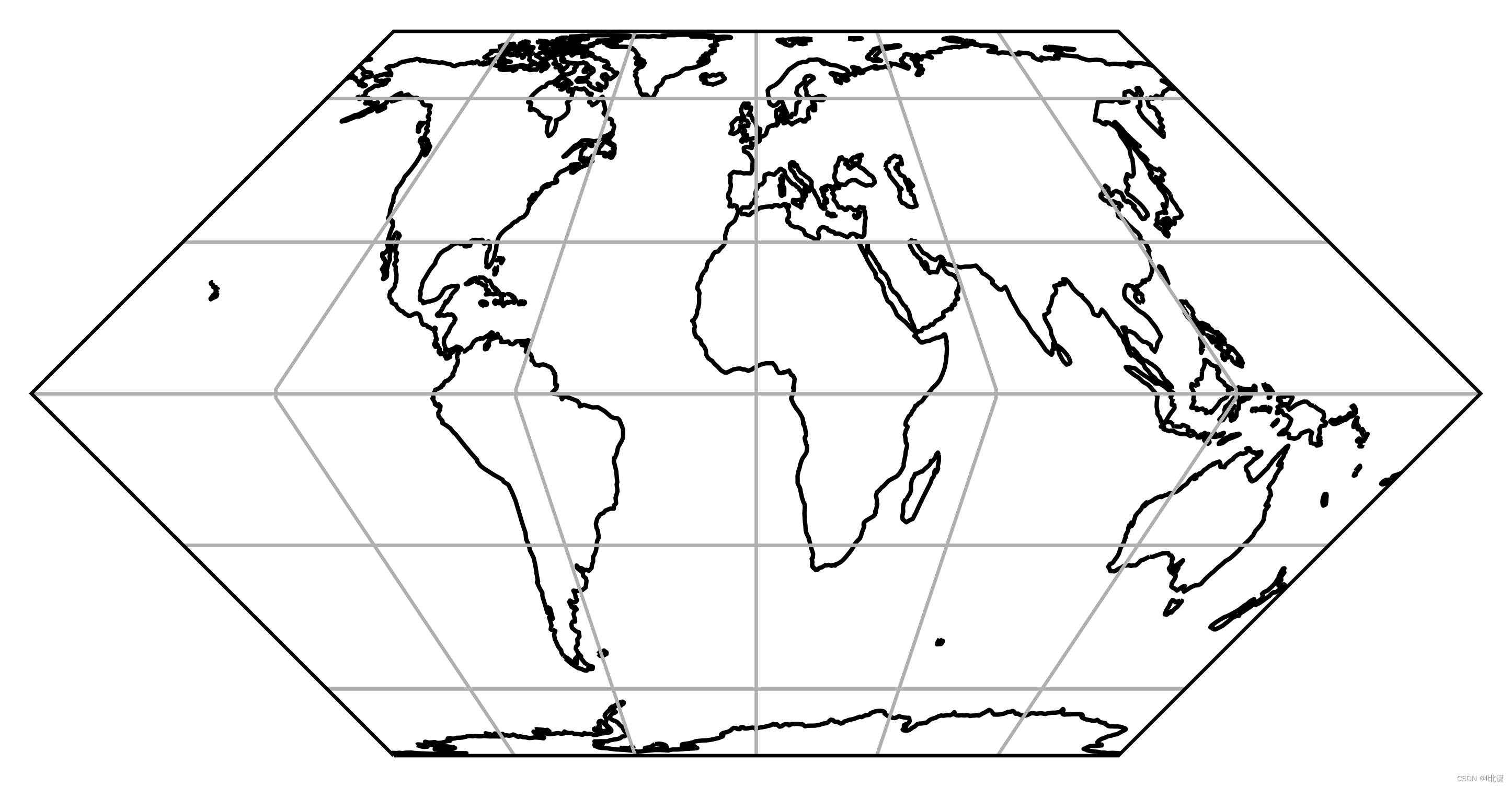
二十四、EckertIII（埃克特第三投影）

伪圆柱投影。纬线是等间距的直线。经线是等间距的椭圆曲线。从中央子午线算起 +/-180° 的经线是半圆形的。极点和中央子午线为直线，其长度是赤道长度的一半。

class cartopy.crs.EckertIII(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.EckertIII())
ax.coastlines(resolution='110m')
ax.gridlines()

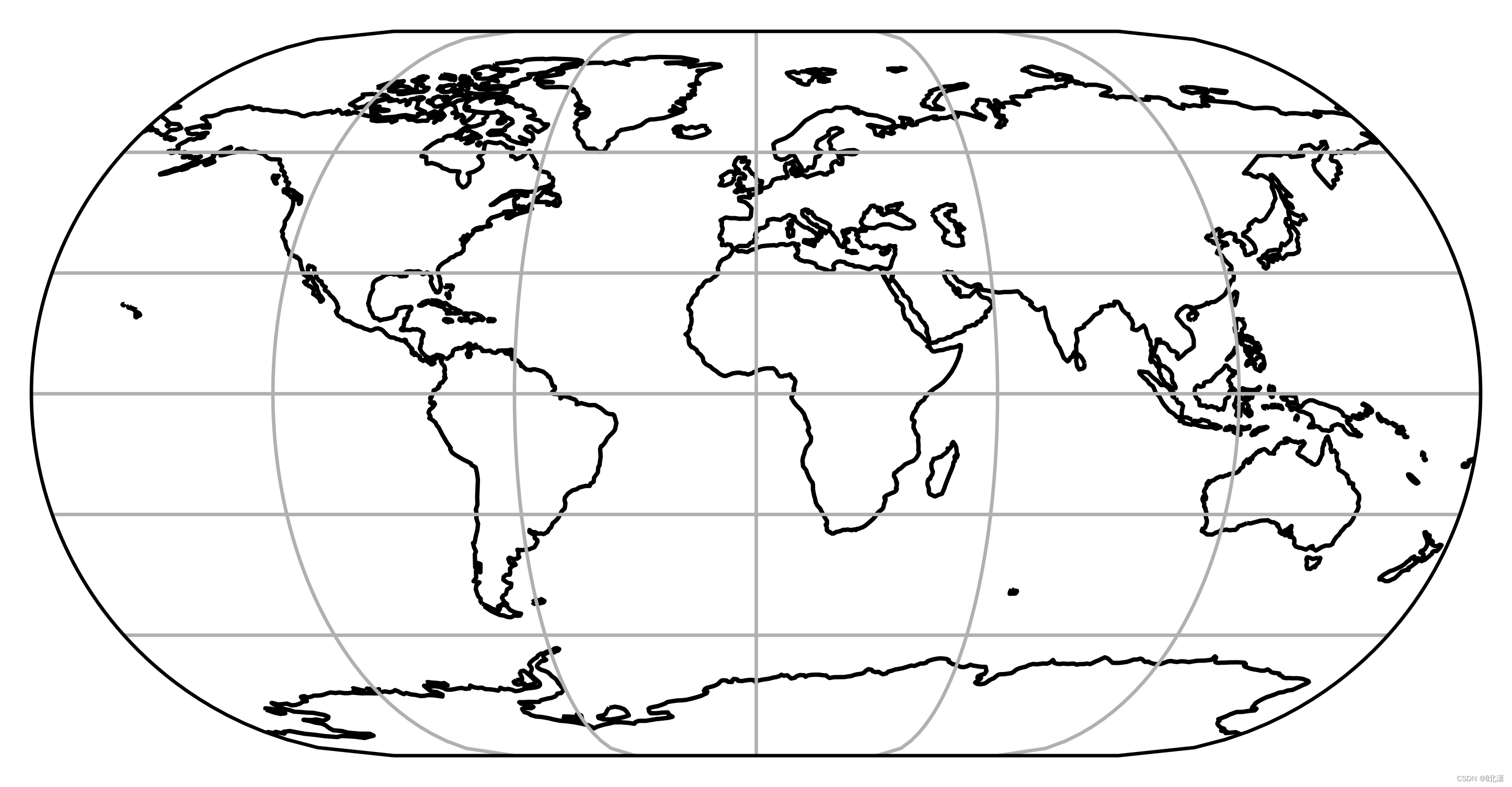
二十五、EckertIV（埃克特第四投影）

伪圆柱等积投影。纬线是非等间距的直线，在极点处较密。经线是等间距的椭圆弧。极点和中央子午线为直线，其长度是赤道长度的一半。

class cartopy.crs.EckertIV(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.EckertIV())
ax.coastlines(resolution='110m')
ax.gridlines()

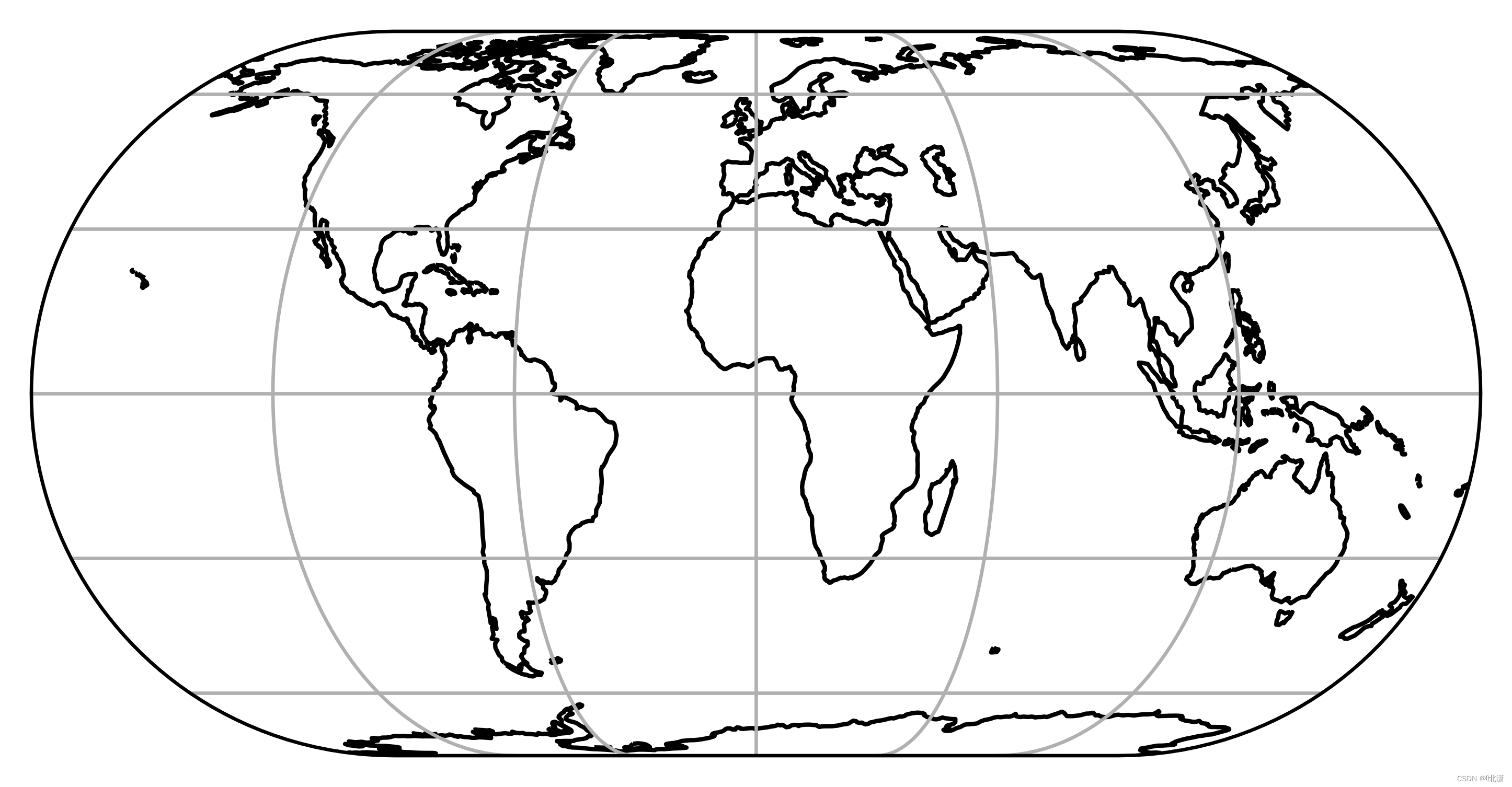
二十六、EckertV（埃克特第五投影）

伪圆柱投影。纬线是等间距的直线。经线是等间距的正弦曲线。极点和中央子午线为直线，其长度是赤道长度的一半。

class cartopy.crs.EckertV(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.EckertV())
ax.coastlines(resolution='110m')
ax.gridlines()

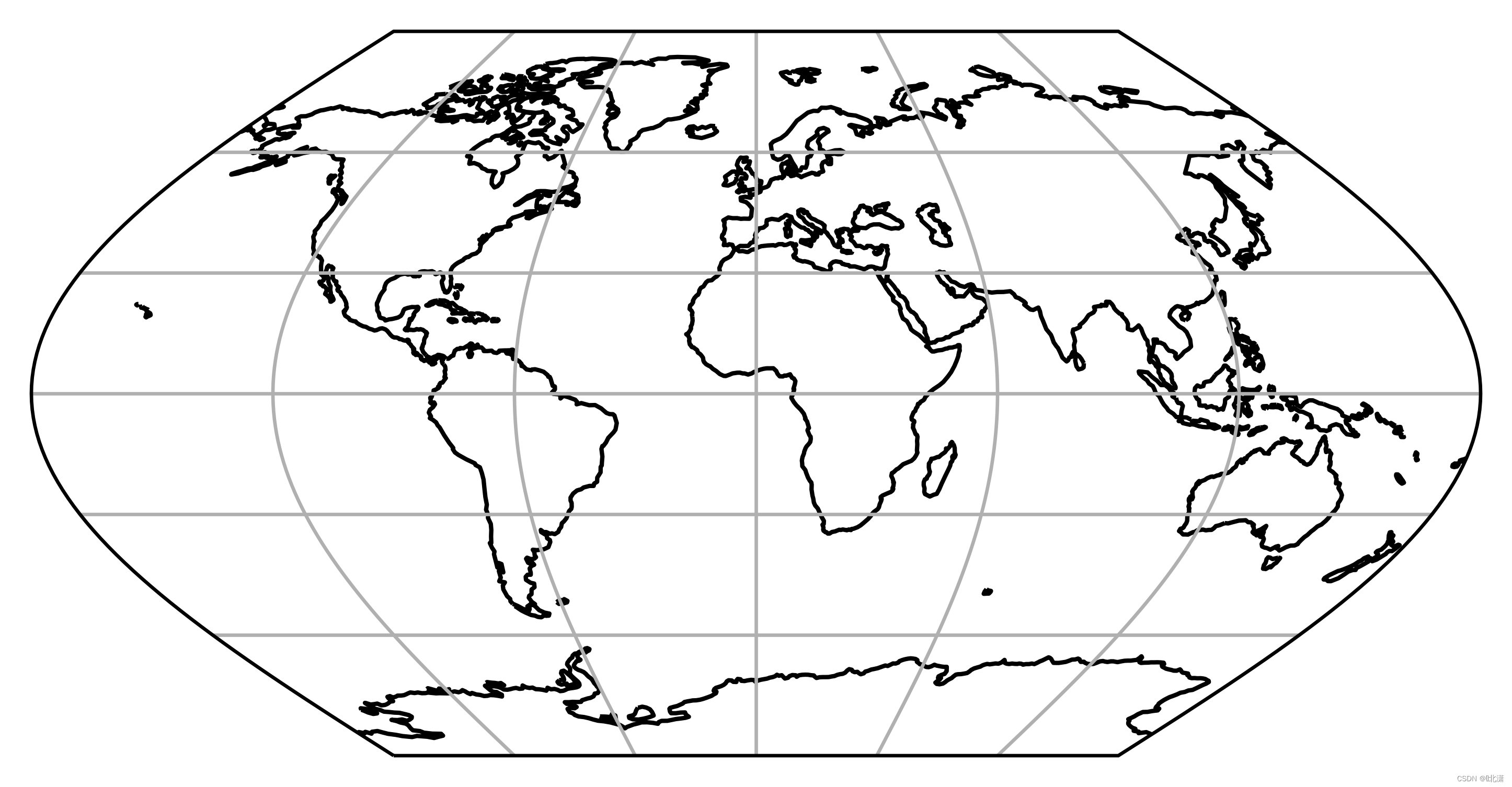
二十七、EckertVI（埃克特第六投影）

伪圆柱等积投影。纬线是非等间距的直线。它们在极点处较密。经线是等间距的正弦曲线。极点和中央子午线为直线，其长度是赤道长度的一半。

class cartopy.crs.EckertVI(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6, 3))
ax = plt.axes(projection=ccrs.EckertVI())
ax.coastlines(resolution='110m')
ax.gridlines()

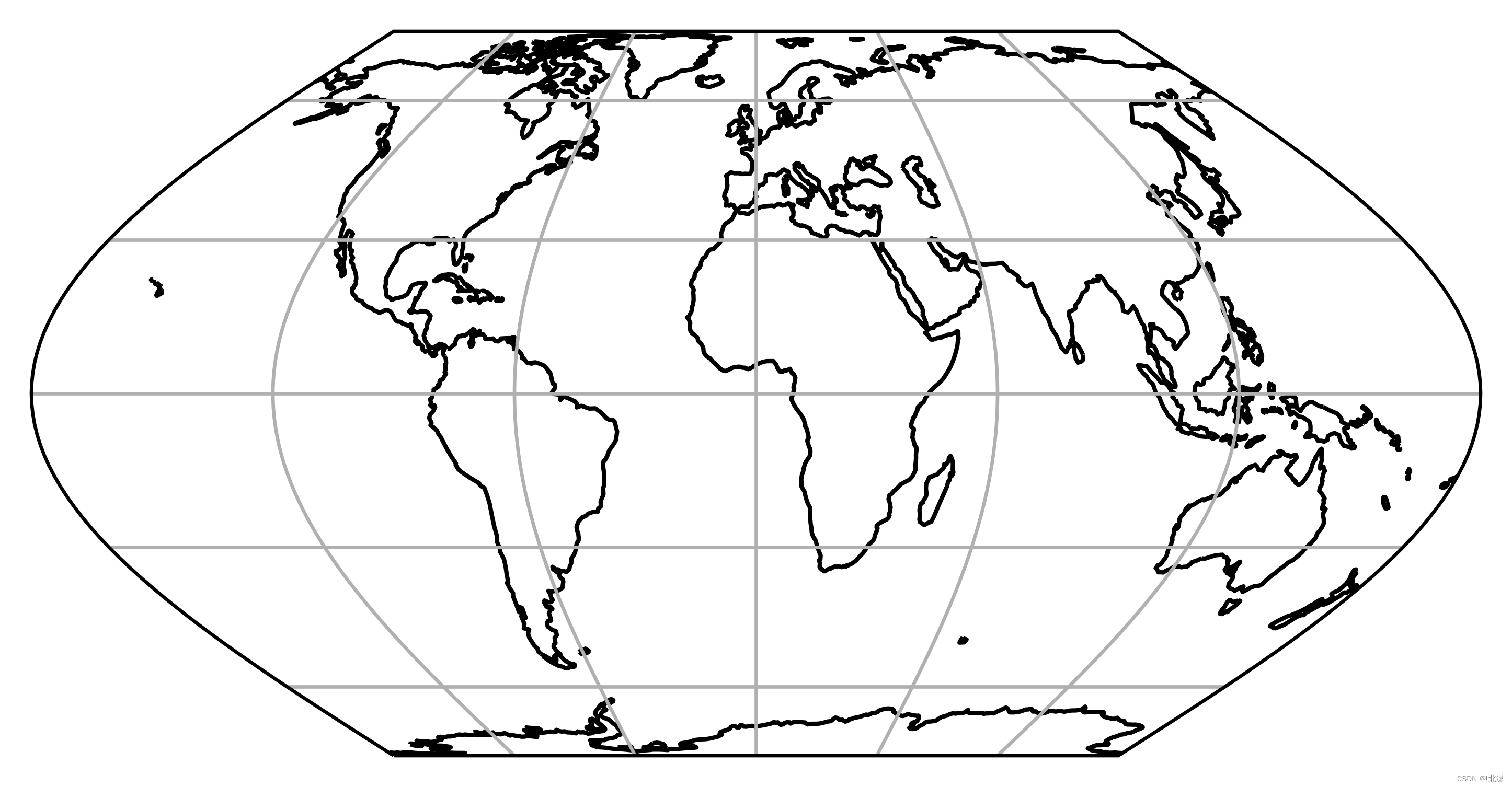
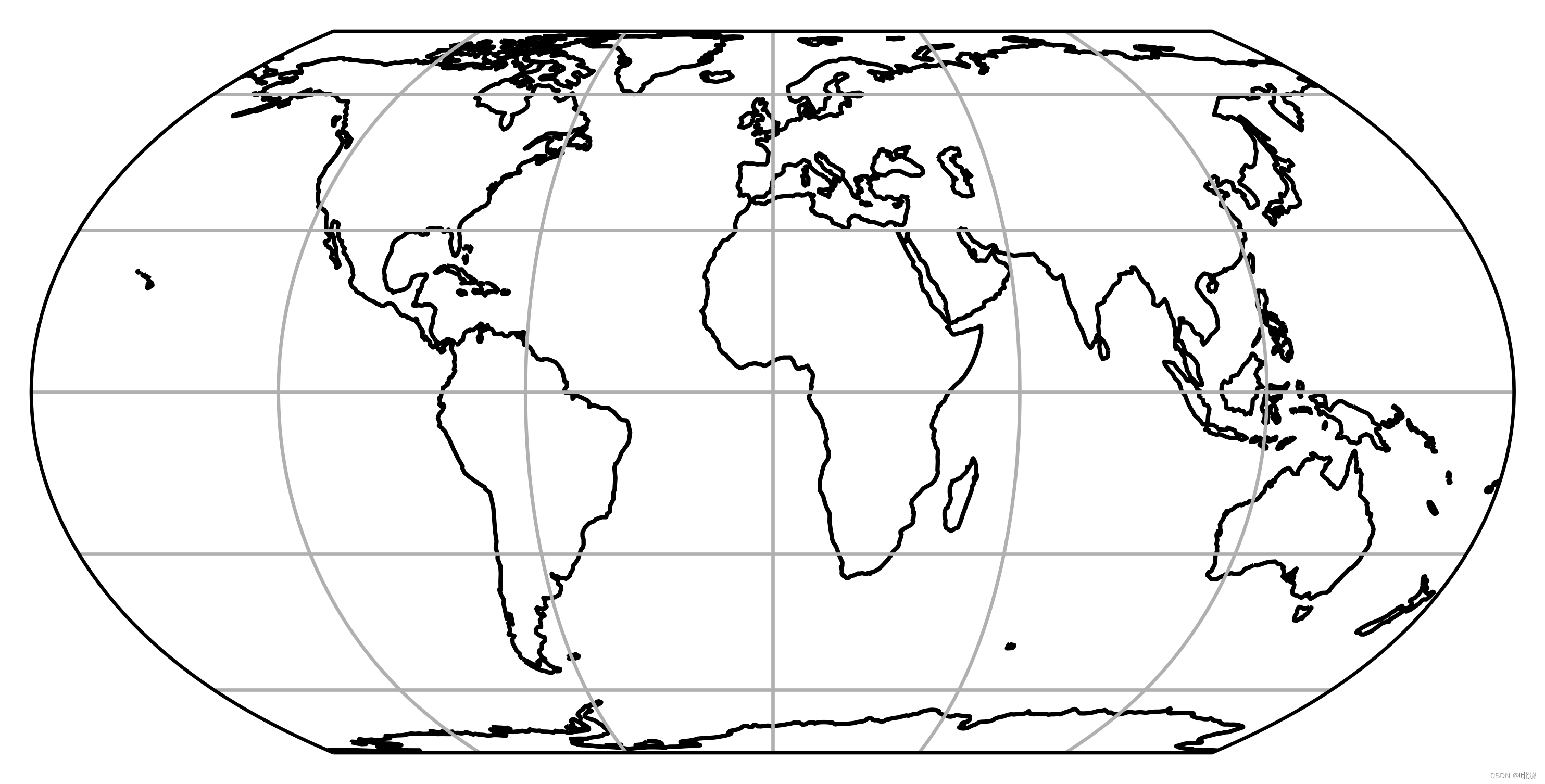
二十八、EqualEarth（等地球投影）

这个投影是伪圆柱的，面积相等。平行线是不等间隔的直线，而子午线是等间隔的弧。它是用来绘制世界地图的。

class cartopy.crs.EqualEarth(central_longitude=0, false_easting=None, false_northing=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(6.1637, 3))
ax = plt.axes(projection=ccrs.EqualEarth())
ax.coastlines(resolution='110m')
ax.gridlines()

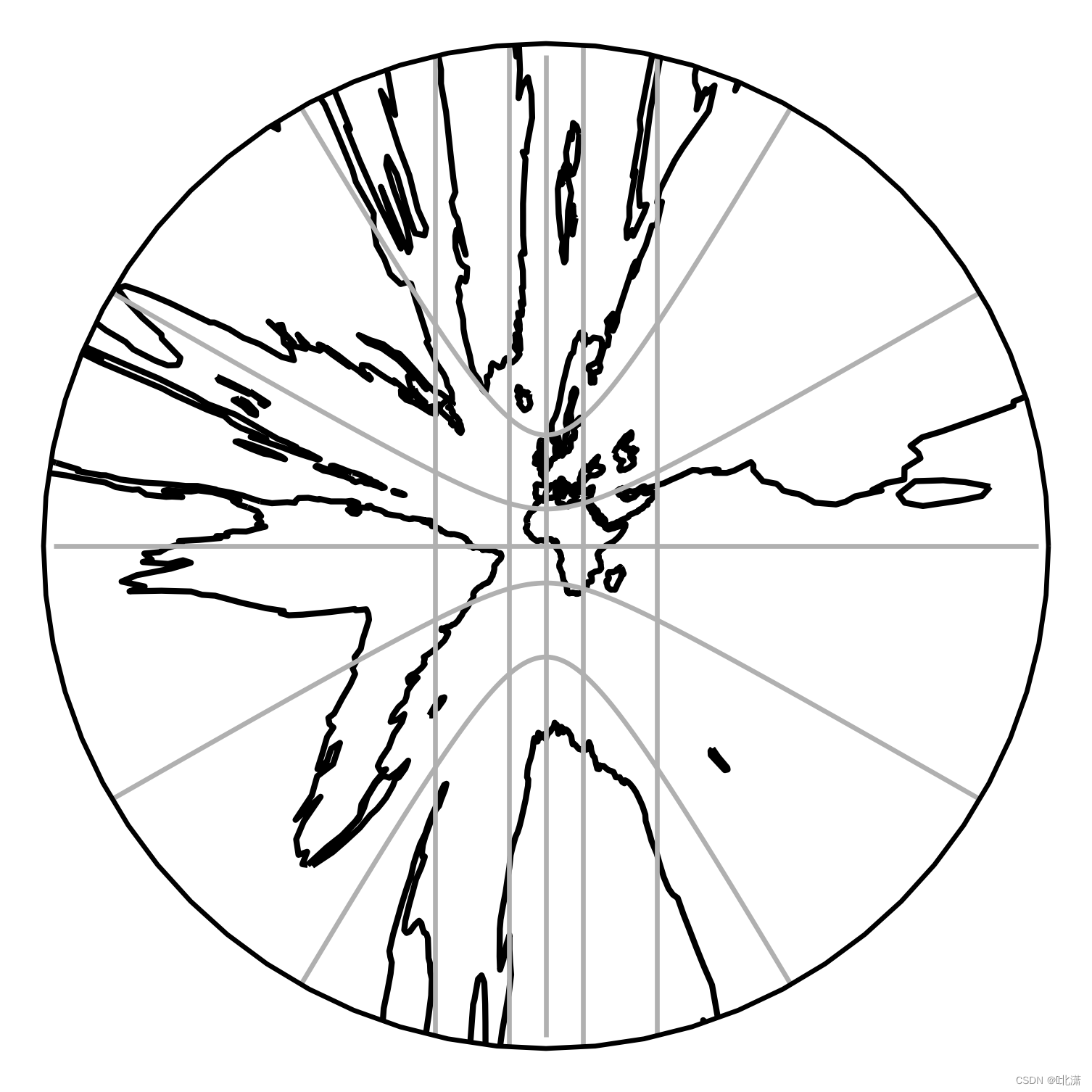
二十九、Gnomonic（球心投影）

此方位投影将地心用作其透视点。无论方位如何，所有的大圆都将投影为直线。此投影适用于导航，因为大圆将突出显示距离最短的路线。

class cartopy.crs.Gnomonic(central_latitude=0.0, central_longitude=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.Gnomonic())
ax.coastlines(resolution='110m')
ax.gridlines()

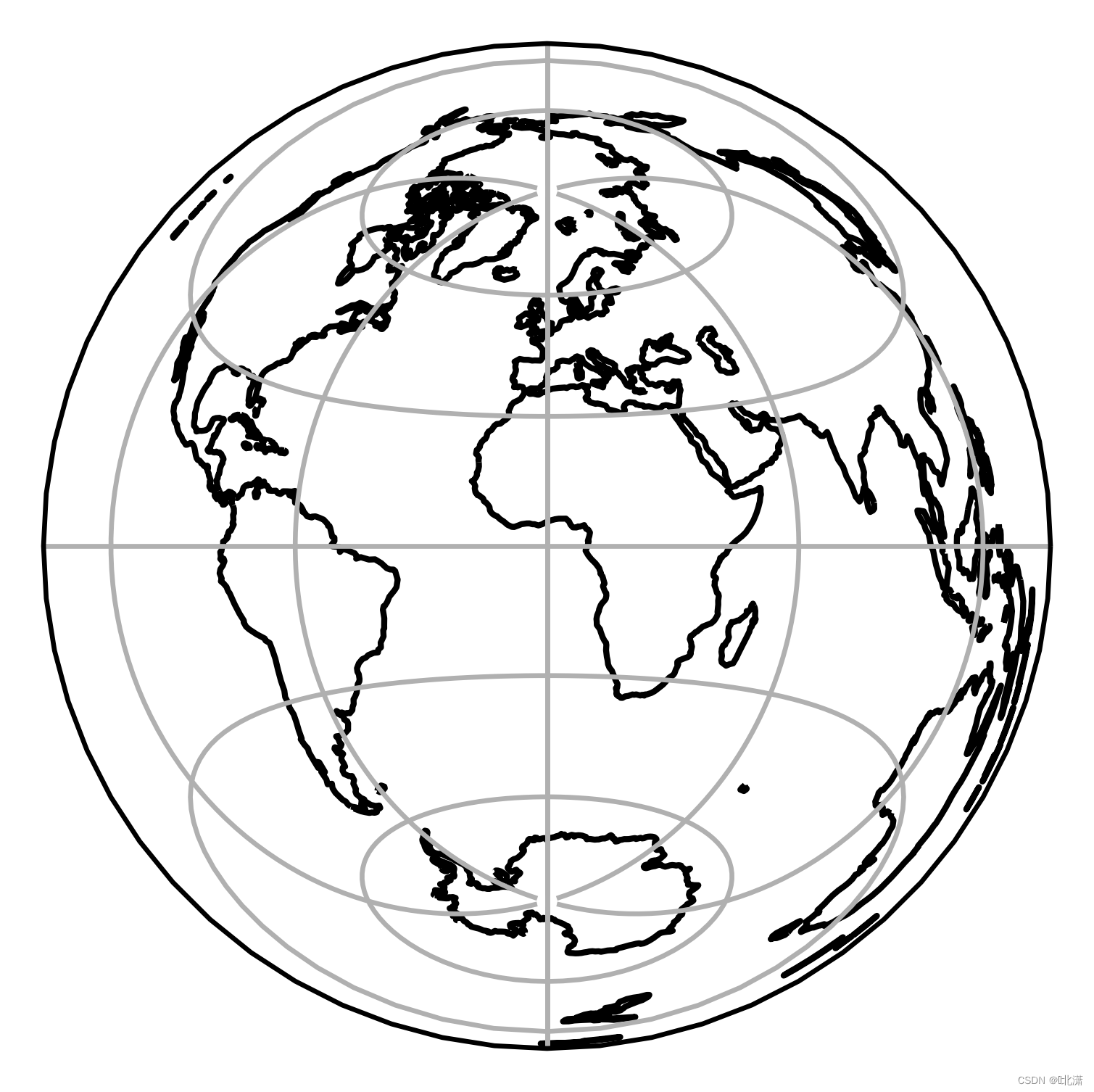
三十、LambertAzimuthalEqualArea（兰伯特方位等积投影）

此投影保留了各多边形的面积，同时也保留了中心的实际方向。变形的常规模式为径向。最适合按比例对称分割的单个地块（圆形或方形）。

class cartopy.crs.LambertAzimuthalEqualArea(central_longitude=0.0, central_latitude=0.0, false_easting=0.0, false_northing=0.0, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3.0066, 3))
ax = plt.axes(projection=ccrs.LambertAzimuthalEqualArea())
ax.coastlines(resolution='110m')
ax.gridlines()

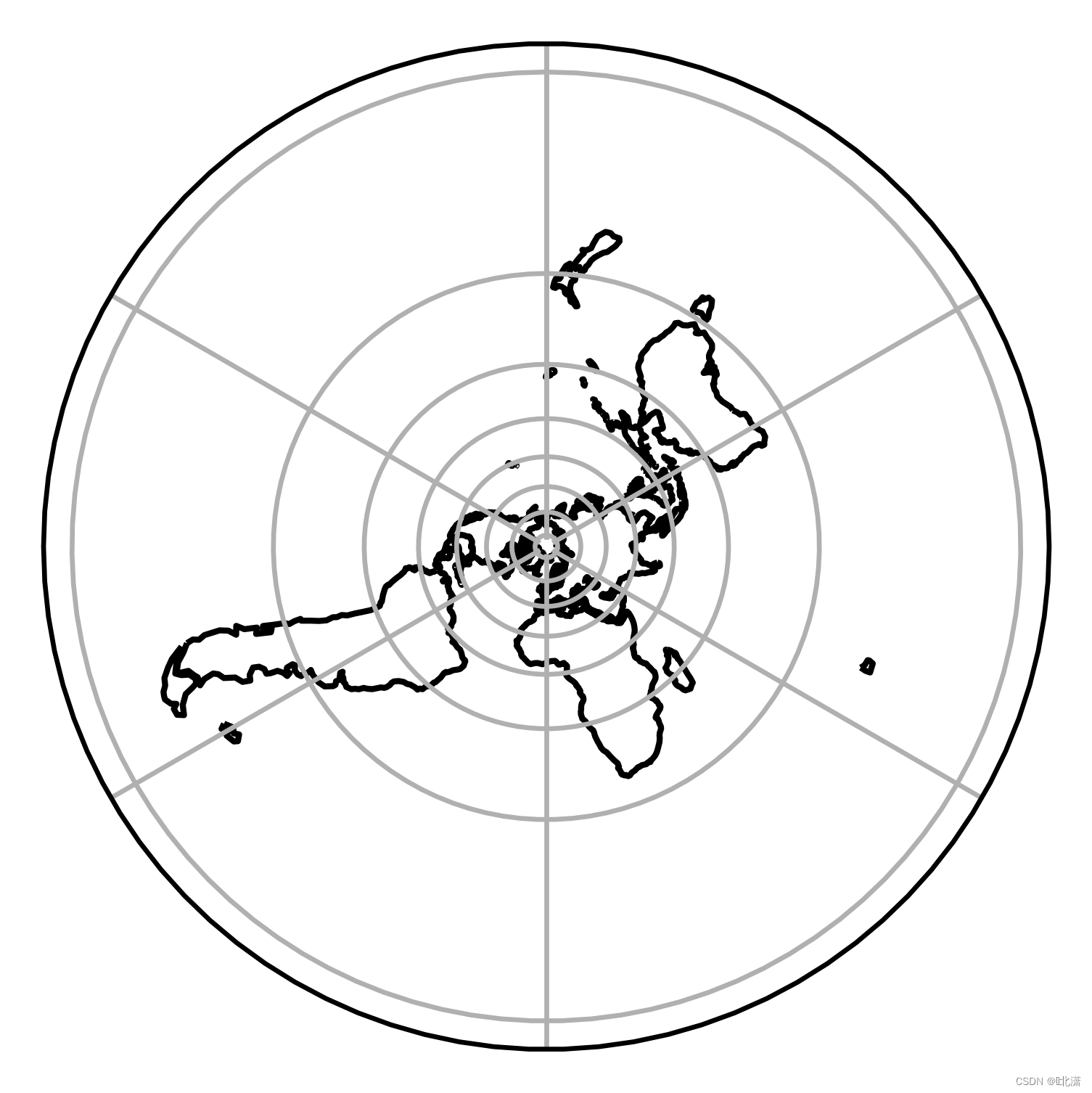
三十一、NorthPolarStereo（北极极射投影）

一种由球面直角坐标系即经纬网通过投影转绘而成的平面网。以投影的极射点及投影平面位置的关系命名。又称乌尔夫网或吴氏网。乌尔夫于1902年首次为结晶学引用了这种投影坐标网图。以球面上一点为极作投影透视点，即极射，把以此点为极的另一个半球面投影在以此为极点的赤道平面上，即赤平。北极极射投影即为以北极为极点进行投影。

class cartopy.crs.NorthPolarStereo(central_longitude=0.0, true_scale_latitude=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.NorthPolarStereo())
ax.coastlines(resolution='110m')
ax.gridlines()

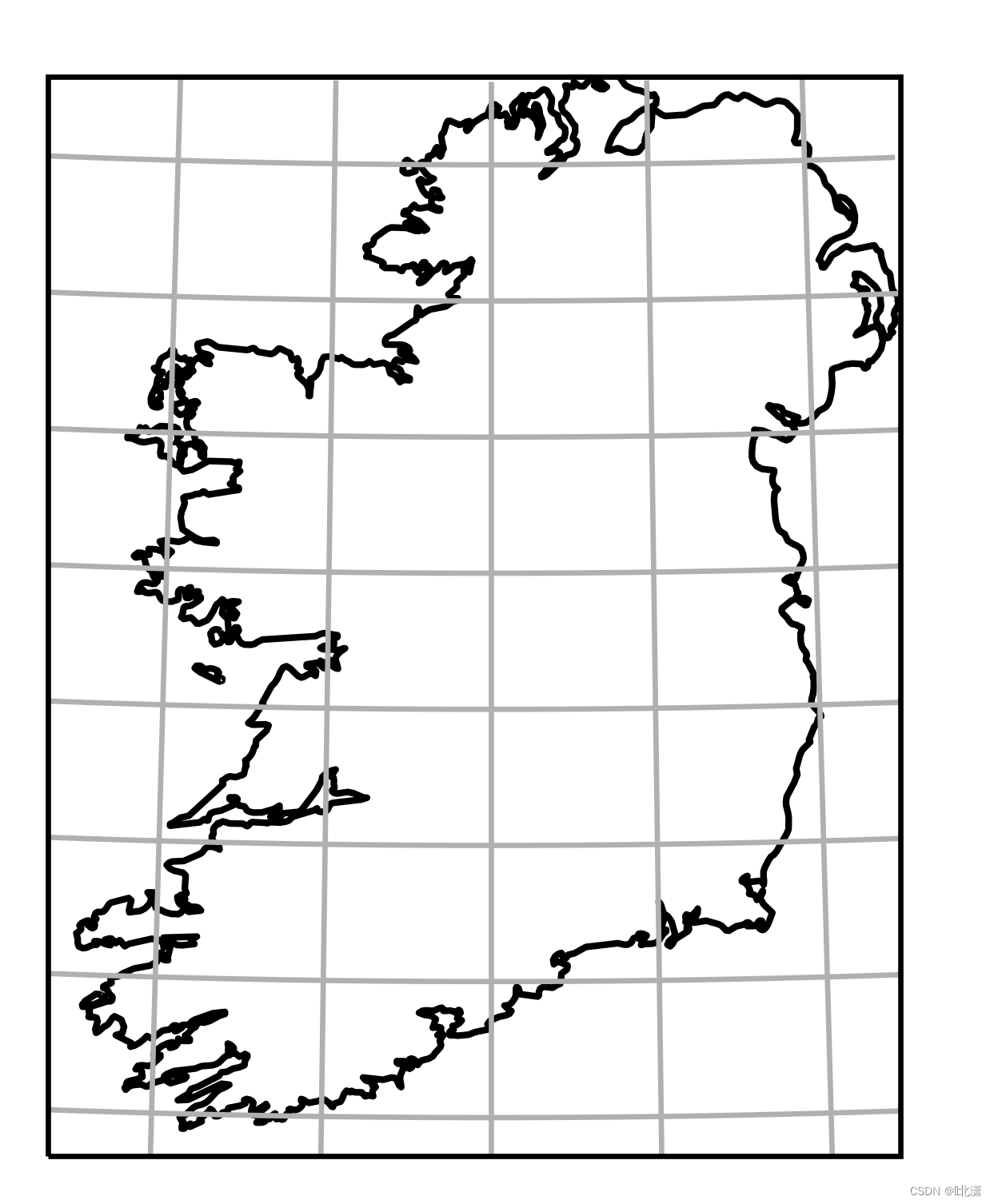
三十二、OSNI（奥斯尼投影）

一种区域性质的等距圆锥投影，用于测绘北爱尔兰岛。

class cartopy.crs.OSNI(approx=False)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(2.4323, 3))
ax = plt.axes(projection=ccrs.OSNI(approx=False))
ax.coastlines(resolution='10m')
ax.gridlines()

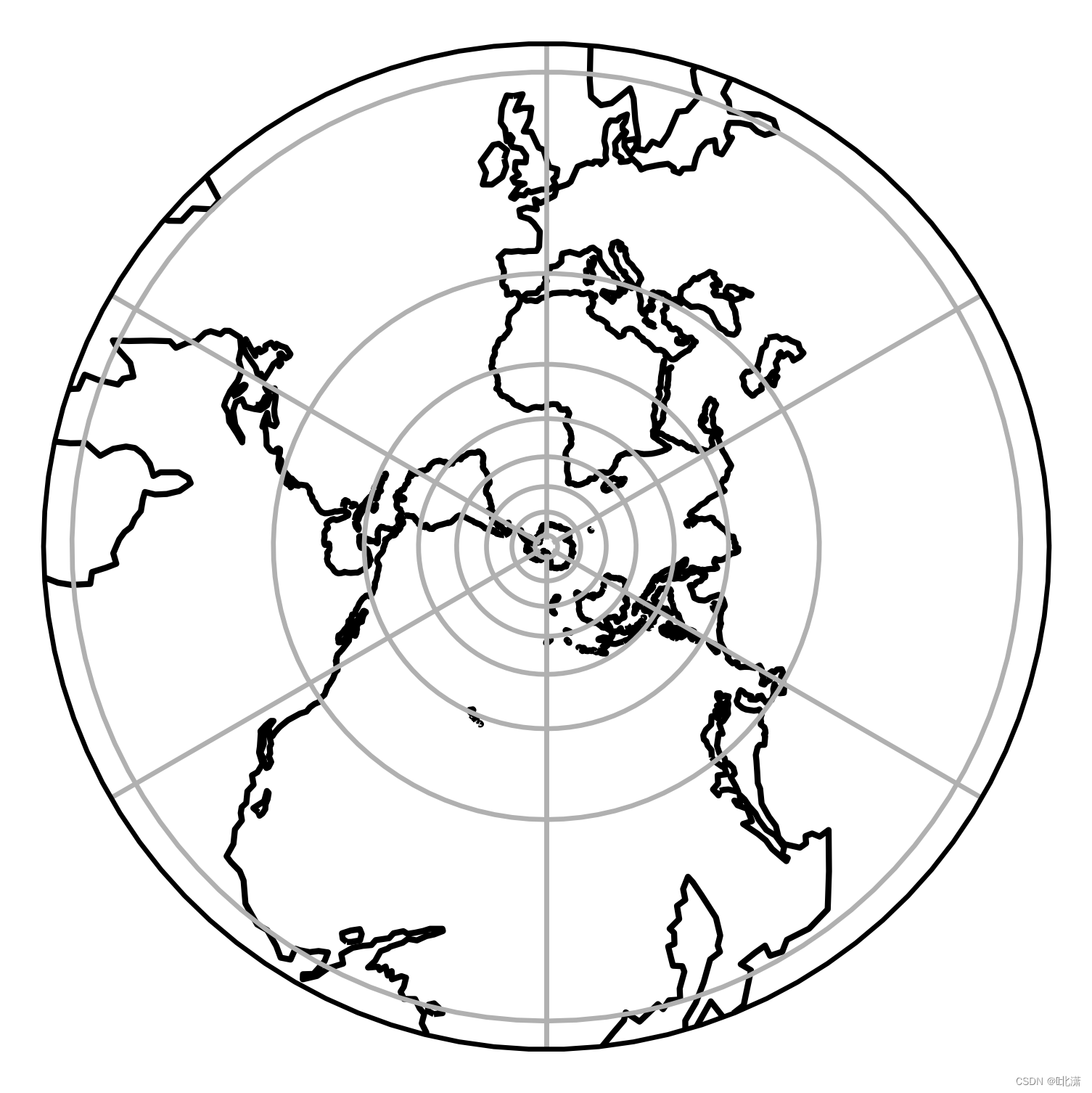
三十三、SouthPolarStereo（南极极射投影）

一种由球面直角坐标系即经纬网通过投影转绘而成的平面网。以投影的极射点及投影平面位置的关系命名。又称乌尔夫网或吴氏网。乌尔夫于1902年首次为结晶学引用了这种投影坐标网图。以球面上一点为极作投影透视点，即极射，把以此点为极的另一个半球面投影在以此为极点的赤道平面上，即赤平。南极极射投影即为以南极为极点进行投影。

class cartopy.crs.SouthPolarStereo(central_longitude=0.0, true_scale_latitude=None, globe=None)

import matplotlib.pyplot as plt
import cartopy.crs as ccrs

plt.figure(figsize=(3, 3))
ax = plt.axes(projection=ccrs.SouthPolarStereo())
ax.coastlines(resolution='110m')
ax.gridlines()

总结

当制图范围较小时，无论什么投影方式都无太大变形；对于范围广大的世界地图、半球地图、大洲地图、大国地图等，则需要慎重考虑。对表现大块区域常用的投影方式可总结为：

世界地图：正圆柱、伪圆柱和多圆锥投影；
东、西半球：常选用横轴方位投影；
南、北半球：常采用正轴方位投影；
水、陆半球：一般选用斜轴方位投影；
极地——正轴方位投影；
赤道附近——横轴方位投影或正轴圆柱投影；
中纬地区——正轴圆锥投影或斜轴方位投影。

---

参考：
（1）https://scitools.org.uk/cartopy/docs/latest/reference/projections.html#
（2）https://www.likecs.com/show-251440.html

---

---

笔者独自运营了微信公众号，用于分享个人学习及工作生活趣事，大家可以关注一波。（微信搜索“微思研”）