D 矩阵
登录—专业IT笔试面试备考平台_牛客网

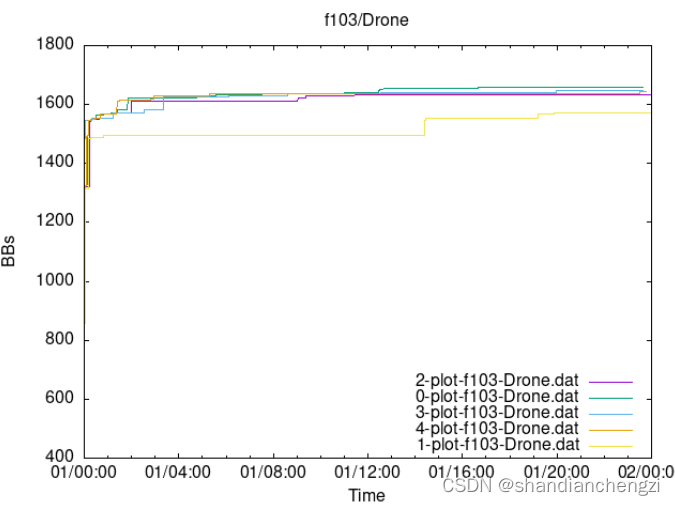
思路:我们能够发现每个点最多只用两种状态,一种是不变,另一种是改变,如果相邻的点与当前点不相同,则可以花费一个单位走过去,否则需要先改变它的状态,然后走过去,能够发现这是一个分层图,一共只有两层,我们直接在分层图上用dijkstra跑最短路即可,当与当前点相邻的点与当前点相同时,距离为2,否则距离为1
// Problem: 矩阵
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/60063/D
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
#include<iostream>
#include<cstring>
#include<string>
#include<sstream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<vector>
#include<set>
#include<unordered_map>
#include<ctime>
#include<cstdlib>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
typedef pair<int,pair<int,int> > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}
int T,hackT;
int n,m,k;
char str[1010][1010];
int dist[1010][1010][2];
bool st[1010][1010][2];
int dx[]={-1,1,0,0},dy[]={0,0,-1,1};
struct Node{
int x,y;
int ans;
int temp;
};
void dijkstra() {
memset(dist,0x3f,sizeof dist);
queue<Node> q;
q.push({1,1,0,str[1][1]-'0'});
dist[1][1][str[1][1]-'0']=0;
while(q.size()) {
auto it=q.front();
q.pop();
int x=it.x,y=it.y,k=it.temp;
if(st[x][y][k]) continue;
st[x][y][k]=true;
for(int i=0;i<4;i++) {
int tx=x+dx[i],ty=y+dy[i];
if(tx<1||tx>n||ty<1||ty>m) continue;
if(k==str[tx][ty]-'0') {
if(dist[tx][ty][k^1]>dist[x][y][k]+2) {
dist[tx][ty][k^1]=dist[x][y][k]+2;
q.push({tx,ty,dist[tx][ty][k^1],k^1});
}
}else {
if(dist[tx][ty][str[tx][ty]-'0']>dist[x][y][k]+1) {
dist[tx][ty][str[tx][ty]-'0']=dist[x][y][k]+1;
q.push({tx,ty,dist[tx][ty][str[tx][ty]-'0'],str[tx][ty]-'0'});
}
}
}
}
}
void solve() {
n=read(),m=read();
for(int i=1;i<=n;i++) scanf("%s",str[i]+1);
dijkstra();
printf("%d\n",min(dist[n][m][0],dist[n][m][1]));
}
int main() {
// init();
// stin();
// scanf("%d",&T);
T=1;
while(T--) hackT++,solve();
return 0;
}
E 数数
登录—专业IT笔试面试备考平台_牛客网
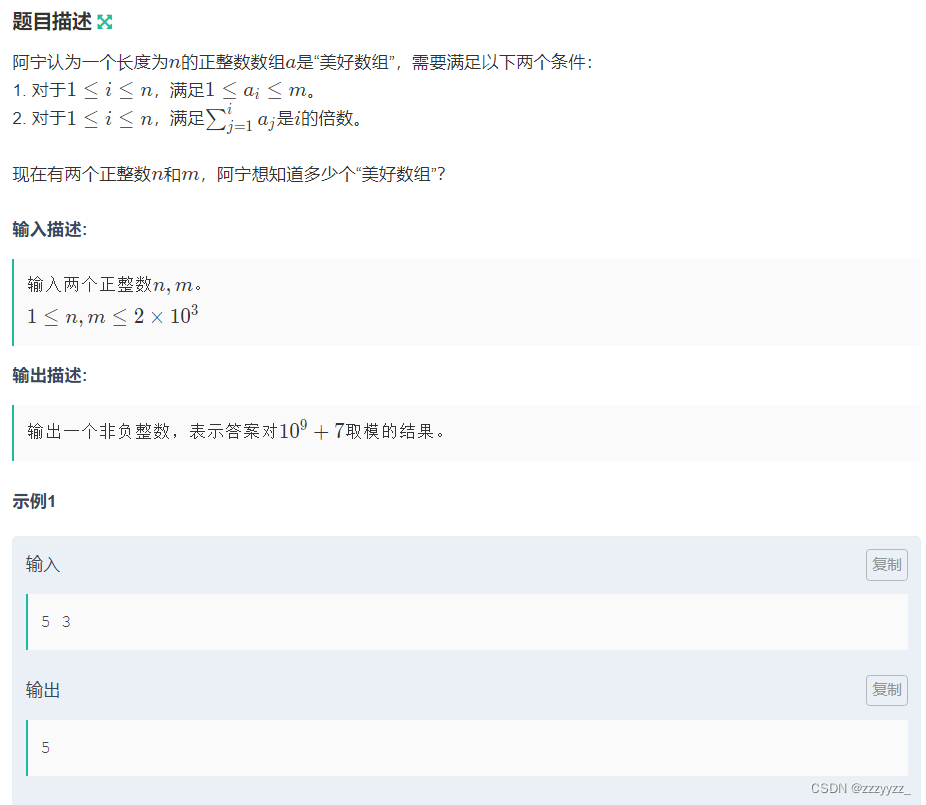
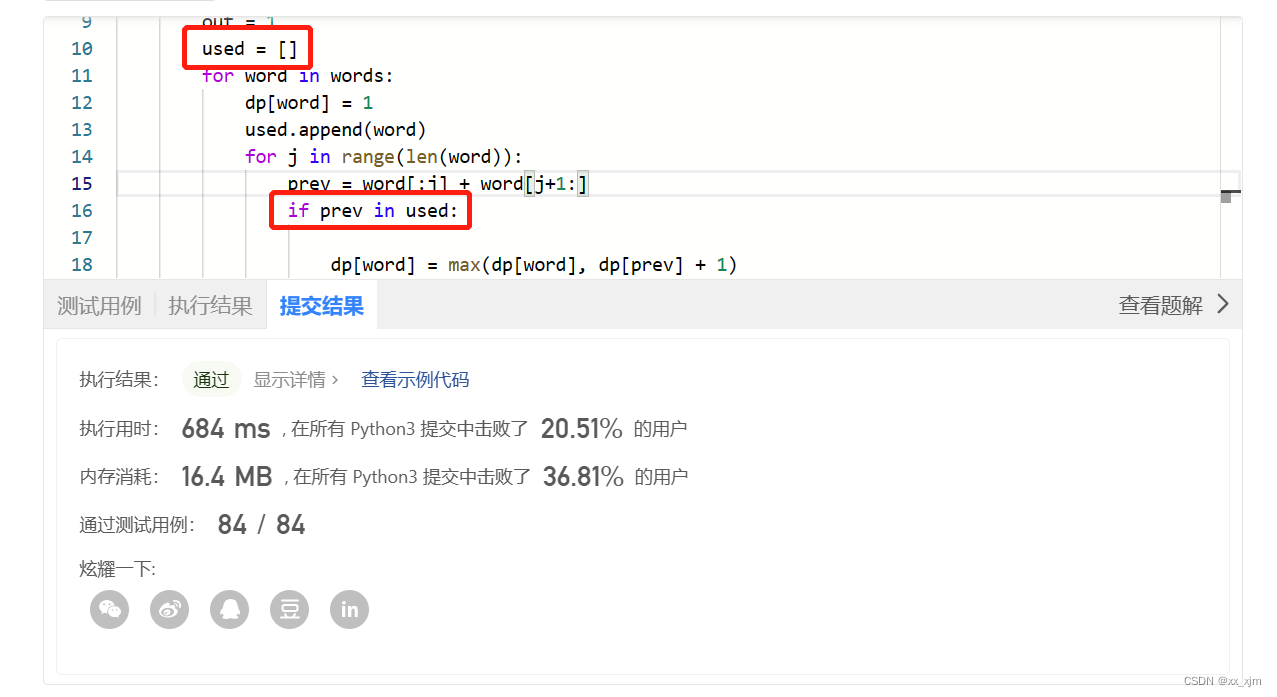
思路:其实能够发现这是一个dp问题,因为如果我知道了当前的总和是什么,当前这个位置方哪个数,那么我们就可以根据前面的状态求出来,一开始是用f[i][j]表示的是只用前i个,并且总和是j的方案数,不仅超时而且还不对,看了题解发现可以f[i][j]表示只使用前i个并且总和为i*j的方案数,因为一定要保证前缀和是i的倍数,假设前i-1个数的和为(i-1)*k,第i个数为t,那么我们能够得到(i-1)*k+t=i*j,能够得到t的值,又因为1<=t<=m,将前式解的的解带入后面能够接出来一个k的范围,(i*j-m+i-2)/(i-1)<=k<=(i*j-1)/(i-1),如果我们知道了i,j那么我们就知道了满足条件的k的范围,那么f[i][j]就能够通过f[i-1][k]求和得到
// Problem: 数数
// Contest: NowCoder
// URL: https://ac.nowcoder.com/acm/contest/60063/E
// Memory Limit: 524288 MB
// Time Limit: 2000 ms
#include<iostream>
#include<cstring>
#include<string>
#include<sstream>
#include<cmath>
#include<cstdio>
#include<algorithm>
#include<queue>
#include<map>
#include<stack>
#include<vector>
#include<set>
#include<unordered_map>
#include<ctime>
#include<cstdlib>
#define fi first
#define se second
#define i128 __int128
using namespace std;
typedef long long ll;
typedef double db;
typedef pair<int,int> PII;
typedef pair<int,pair<int,int> > PIII;
const double eps=1e-7;
const int N=5e5+7 ,M=5e5+7, INF=0x3f3f3f3f,mod=1e9+7;
const long long int llINF=0x3f3f3f3f3f3f3f3f;
inline ll read() {ll x=0,f=1;char c=getchar();while(c<'0'||c>'9') {if(c=='-') f=-1;c=getchar();}
while(c>='0'&&c<='9') {x=(ll)x*10+c-'0';c=getchar();} return x*f;}
inline void write(ll x) {if(x < 0) {putchar('-'); x = -x;}if(x >= 10) write(x / 10);putchar(x % 10 + '0');}
inline void write(ll x,char ch) {write(x);putchar(ch);}
void stin() {freopen("in_put.txt","r",stdin);freopen("my_out_put.txt","w",stdout);}
bool cmp0(int a,int b) {return a>b;}
template<typename T> T gcd(T a,T b) {return b==0?a:gcd(b,a%b);}
template<typename T> T lcm(T a,T b) {return a*b/gcd(a,b);}
void hack() {printf("\n----------------------------------\n");}
int T,hackT;
int n,m,k;
int f[1010][1010];
int sum[1010];
void solve() {
n=read(),m=read();
for(int i=1;i<=m;i++) f[1][i]=1;
for(int i=2;i<=n;i++) {
for(int j=1;j<=m;j++) sum[j]=(sum[j-1]+f[i-1][j])%mod;
for(int j=1;j<=m;j++) {
int l=(i*j-m+i-2)/(i-1),r=(i*j-1)/(i-1);
l=max(l,1),r=min(r,m);
f[i][j]=(sum[r]-sum[l-1]+mod)%mod;
}
}
ll res=0;
for(int i=1;i<=m;i++) res=(res+f[n][i])%mod;
write(res);
}
int main() {
// init();
// stin();
// scanf("%d",&T);
T=1;
while(T--) hackT++,solve();
return 0;
}