《机器学习公式推导与代码实现》chapter21-贝叶斯概率模型

news2024/9/24 3:25:54

《机器学习公式推导与代码实现》学习笔记，记录一下自己的学习过程，详细的内容请大家购买作者的书籍查阅。

贝叶斯概率模型

1 贝叶斯定理简介

贝叶斯定理认为任意未知量 $\theta$ 都可以看做一个随机变量，对该未知量的描述可以用一个概率分布 $\pi \left(\theta \right)$ 来概况，这是贝叶斯学派最基本的观点。当这个概率分布在进行现场试验或抽样前已经确定时，便可将该分布成为先验概率分布，再结合由给定数据集 $X$ 计算样本的似然函数$L\left ( \theta \mid X \right ) $后，即可应用贝叶斯公式计算该未知量的后验概率分布。经典的贝叶斯公式如下：
$\pi \left(\theta \mid X\right) = \frac{L\left ( \theta \mid X \right )\pi\left(\theta\right)}{\int L\left ( \theta \mid X \right )\pi\left(\theta\right)d\theta}$
其中 $\pi \left(\theta \mid X\right)$ 为后验概率， $\int L\left ( \theta \mid X \right )\pi\left(\theta\right)d\theta$ 为边缘分布，其排除了任何有关未知量 $\theta$ 的信息，因此贝叶斯公式的等价形式可以写作：
$\pi \left(\theta \mid X\right) \propto L\left ( \theta \mid X \right )\pi\left(\theta\right)$
贝叶斯公式的本质就是基于先验概率分布 $\pi\left(\theta\right)$ 和似然函数 $L\left ( \theta \mid X \right )$ 的统计推断，其中先验概率分布 $\pi\left(\theta\right)$ 的选择和后验分布 $\pi \left(\theta \mid X\right)$ 的推断是贝叶斯领域的两个核心问题。

朴素贝叶斯是一种基于贝叶斯定理的概率分类模型，而贝叶斯网络是一种将贝叶斯定理应用于概率图中的分类模型，二者都是生成式学习方法。

之所以取名朴素贝叶斯是因为特征的条件独立性假设能够大大简化算法的学习和预测过程，但也会造成一定的精度损失。

进一步的，将朴素贝叶斯的条件独立性假设去掉，认为特征之间存在相关性的贝叶斯模型就是贝叶斯网络模型，贝叶斯网络模型是一种概率有向图模型。

2 朴素贝叶斯

在这里插入图片描述

2.1 基于numpy的朴素贝叶斯实现

import numpy as np

# 朴素贝叶斯模型训练与预测
class NaiveBayes:

    def fit(self, X, y):
        
        self.classes = y[y.columns[0]].unique() # 标签类别
        self.class_count = y[y.columns[0]].value_counts() # 类先验概率分布
        self.class_prior = self.class_count / len(y) # 极大似然估计：类先验概率
        self.prior_condition_prob = dict() # 类条件概率字典初始化

        # 遍历计算类条件概率
        for col in X.columns: # 遍历特征
            for j in self.classes: # 遍历类别
                p_x_y = X[(y==j).values][col].value_counts() # 统计当前类别下特征的不同取值
                for i in p_x_y.index: # 遍历计算类条件概率
                    self.prior_condition_prob[(col, i, j)] = p_x_y[i] / self.class_count[j]
        
        return self.classes, self.class_prior, self.prior_condition_prob # 标签类别，类先验概率分布，类条件概率分布

    def predict(self, X_test):

        res = [] # 初始化结果列表
        for c in self.classes: # 遍历样本类别
            p_y = self.class_prior[c] # 获取当前类的先验概率
            p_x_y = 1 # 初始化类条件概率
            for i in X_test.items(): # 似然函数：类条件概率连乘
                p_x_y *= self.prior_condition_prob[tuple(list(i)+[c])]
            res.append(p_y * p_x_y) # 类先验概率与类条件概率乘积
        print(res)
        return self.classes[np.argmax(res)] # 结果转化为预测类别

构造数据集

import pandas as pd

# 构造数据集: 来自于李航统计学习方法表4.1
x1 = [1,1,1,1,1,2,2,2,2,2,3,3,3,3,3] # 特征x1
x2 = ['S','M','M','S','S','S','M','M','L','L','L','M','M','L','L'] # 特征x2
y = [-1,-1,1,1,-1,-1,-1,1,1,1,1,1,1,1,-1] # 标签列表

df = pd.DataFrame({'x1':x1, 'x2':x2, 'y':y})
df.head()

在这里插入图片描述
测试结果

model = NaiveBayes()
X = df[['x1', 'x2']]
y = df[['y']]
classes, class_prior, prior_condition_prob = model.fit(X, y)
classes, class_prior, prior_condition_prob

(array([-1,  1], dtype=int64),
  1    0.6
 -1    0.4
 Name: y, dtype: float64,
 {('x1', 1, -1): 0.5,
  ('x1', 2, -1): 0.3333333333333333,
  ('x1', 3, -1): 0.16666666666666666,
  ('x1', 3, 1): 0.4444444444444444,
  ('x1', 2, 1): 0.3333333333333333,
  ('x1', 1, 1): 0.2222222222222222,
  ('x2', 'S', -1): 0.5,
  ('x2', 'M', -1): 0.3333333333333333,
  ('x2', 'L', -1): 0.16666666666666666,
  ('x2', 'M', 1): 0.4444444444444444,
  ('x2', 'L', 1): 0.4444444444444444,
  ('x2', 'S', 1): 0.1111111111111111})

X_test = {'x1': 2, 'x2': 'S'}
print('测试数据预测类别为：', model.predict(X_test))

[0.06666666666666667, 0.02222222222222222]
测试数据预测类别为： -1

2.2 基于sklearn的朴素贝叶斯实现

sklearn也提供了朴素贝叶斯的算法实现方式，涵盖不同似然函数分布的朴素贝叶斯算法实现方式，比如高斯朴素贝叶斯、伯努利朴素贝叶斯、多项式朴素贝叶斯等，我们以高斯朴素贝叶斯为例，高斯朴素贝叶斯即假设似然函数为正态分布的朴素贝叶斯模型，它的似然函数如下：
$P\left(x_{i}\mid y\right)=\frac{1}{\sqrt{2\pi\sigma_{y}^{2}}}exp\left(-\frac{\left(x_{i}-\mu_{y}\right)^{2}}{2\sigma_{y}^{2}}\right)$
sklearn中高斯朴素贝叶斯的调用接口为sklearn.naive_bayes.GaussianNB，以iris数据集为例给出调用示例：

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import GaussianNB
from sklearn.metrics import accuracy_score
X, y = load_iris(return_X_y=True)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
gnb = GaussianNB()
y_pred = gnb.fit(X_train, y_train).predict(X_test)
f"Accuracy of GaussianNB in iris data test: {accuracy_score(y_test, y_pred)}"

'Accuracy of GaussianNB in iris data test: 0.9466666666666667'

3 贝叶斯网络

3.1 贝叶斯网络的原理推导

在这里插入图片描述

3.2 借助于pgmpy的贝叶斯网络实现

pgmpy是一款基于python的概率图模型包，主要包括贝叶斯网络和马尔可夫蒙特卡洛等常见概率图模型的实现以及推断方法。
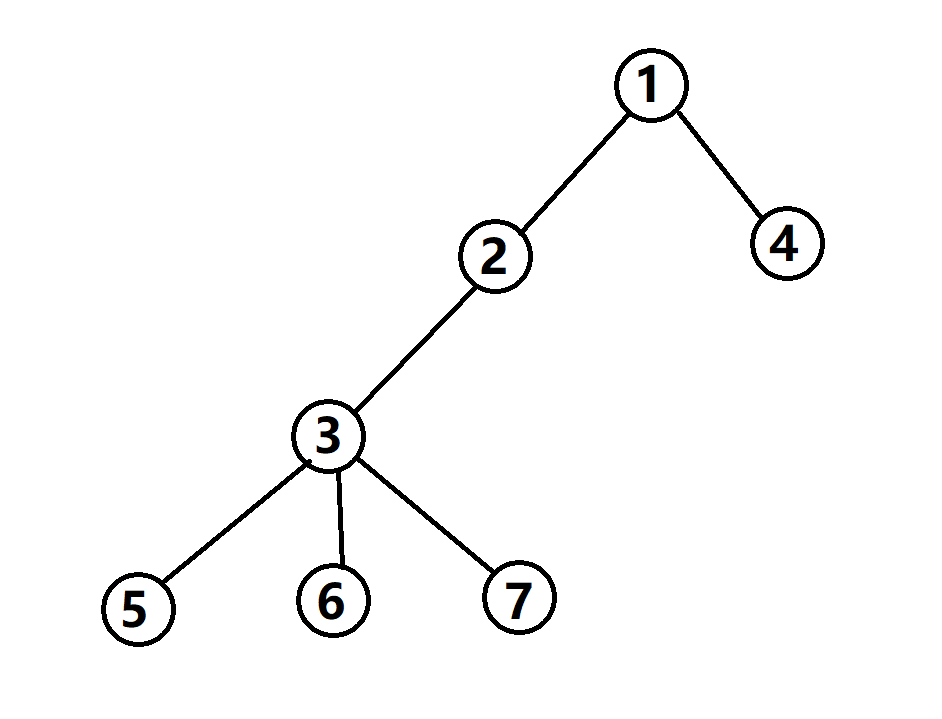
我们以学生获得推荐信的质量为例来构造贝叶斯网络，相关特征的DAG和概率表如图所示：
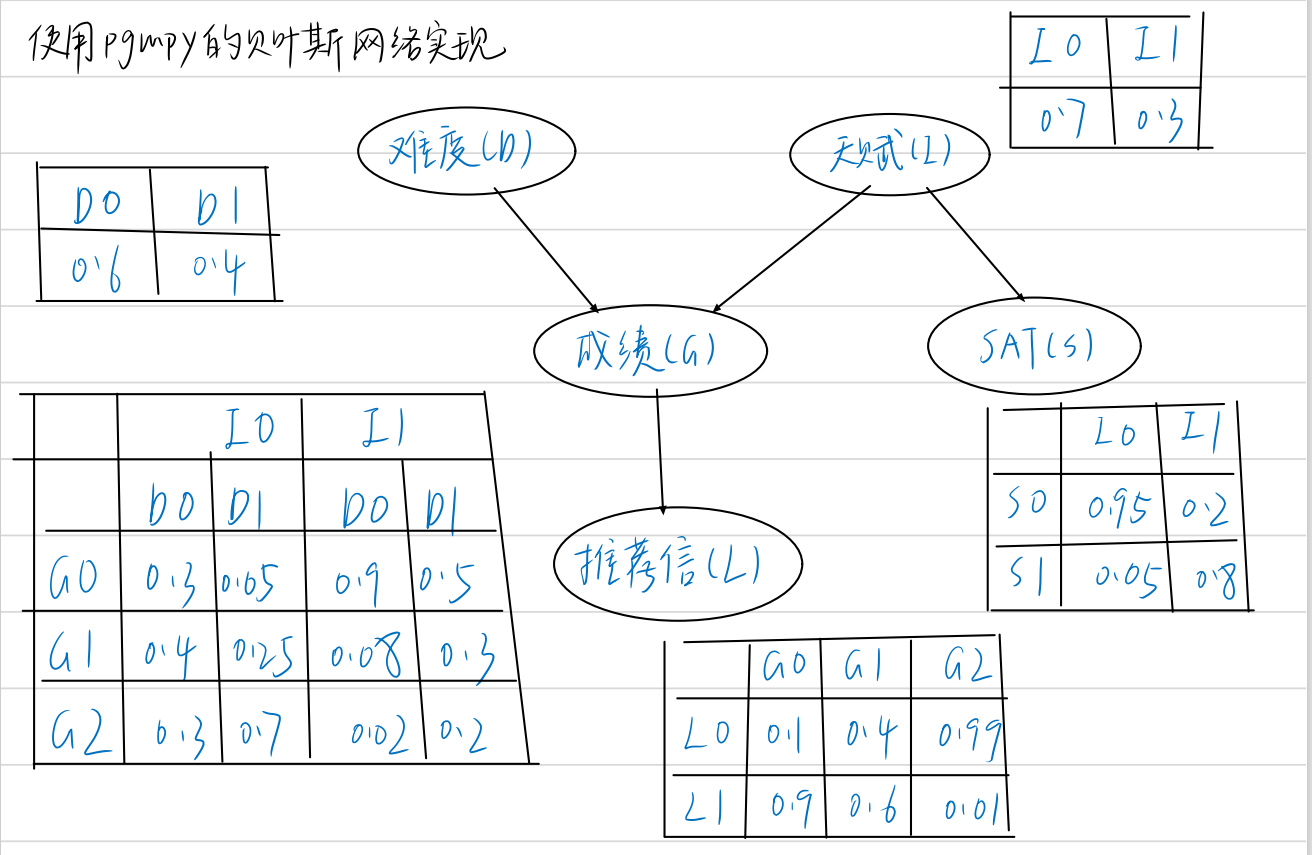
在这里插入图片描述
首先指定各变量之间的关系：

from pgmpy.factors.discrete import TabularCPD
from pgmpy.models import BayesianModel

# 构建模型框架
letter_model = BayesianModel([
    ('D', 'G'),
    ('I', 'G'),
    ('G', 'L'),
    ('I', 'S')
])

构建各个结点的条件概率分布，需要指定相关参数和传入概率表：

# 学生成绩的条件概率分布
grade_cpd = TabularCPD(
    variable='G', # 结点名称
    variable_card=3, # 结点取值个数
    values=[[0.3, 0.05, 0.9, 0.5],
            [0.4, 0.25, 0.08, 0.3],
            [0.3, 0.7, 0.02, 0.2]],
    evidence=['I', 'D'], # 该结点的依赖结点
    evidence_card=[2, 2] # 依赖结点的取值个数
)

# 考试难度的条件概率分布
difficulty_cpd = TabularCPD(
    variable='D',
    variable_card=2,
    values = [[0.6], [0.4]]
)

# 个人天赋的条件概率分布
intel_cpd = TabularCPD(
    variable='I',
    variable_card=2,
    values=[[0.7], [0.3]]
) 

# 推荐信质量的概率分布
letter_cpd = TabularCPD(
    variable='L',
    variable_card=2,
    values = [[0.1, 0.4, 0.99],
              [0.9, 0.6, 0.01]],
    evidence=['G'],
    evidence_card=[3]
)

# sat考试分数的条件概率分布
sat_cpd = TabularCPD(
    variable='S',
    variable_card=2,
    values=[[0.95, 0.2],
            [0.05, 0.8]],
    evidence=['I'],
    evidence_card=[2]
)

构建贝叶斯网络模型

# 将各节点添加到模型中，构建贝叶斯网络
letter_model.add_cpds(
    grade_cpd,
    difficulty_cpd,
    intel_cpd,
    letter_cpd,
    sat_cpd
)

from pgmpy.inference import VariableElimination # 导入pgmpy贝叶斯推断模块
letter_infer = VariableElimination(letter_model) # 贝叶斯网络推断

# 天赋较好且考试不难情况下推断该学生获得推荐信的质量
prob_G = letter_infer.query(
    variables=['G'],
    evidence={'I':1, 'D':0}
)
print(prob_G) # 聪明学生遇到简单考试获得一等成绩的概率高达90%

+------+----------+
| G    |   phi(G) |
+======+==========+
| G(0) |   0.9000 |
+------+----------+
| G(1) |   0.0800 |
+------+----------+
| G(2) |   0.0200 |
+------+----------+