题目

在一个大小为 n 且 n 为偶数的链表中，对于 0 <= i <= (n / 2) - 1 的 i ，第 i 个节点（下标从 0 开始）的孪生节点为第 (n-1-i) 个节点。

比方说，n = 4 那么节点 0 是节点 3 的孪生节点，节点 1 是节点 2 的孪生节点。这是长度为 n = 4 的链表中所有的孪生节点。
孪生和定义为一个节点和它孪生节点两者值之和。

给你一个长度为偶数的链表的头节点 head ，请你返回链表的最大孪生和。

示例 1：

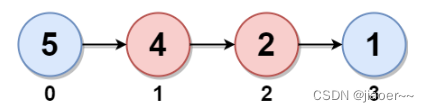
输入：head = [5,4,2,1]
输出：6
解释：
节点 0 和节点 1 分别是节点 3 和 2 的孪生节点。孪生和都为 6 。
链表中没有其他孪生节点。
所以，链表的最大孪生和是 6 。

示例 2：

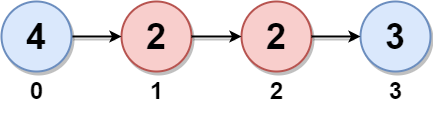
输入：head = [4,2,2,3]
输出：7
解释：
链表中的孪生节点为：
- 节点 0 是节点 3 的孪生节点，孪生和为 4 + 3 = 7 。
- 节点 1 是节点 2 的孪生节点，孪生和为 2 + 2 = 4 。
所以，最大孪生和为 max(7, 4) = 7 。

示例 3：

输入：head = [1,100000]
输出：100001
解释：
链表中只有一对孪生节点，孪生和为 1 + 100000 = 100001 。

提示：

链表的节点数目是 [2, 105] 中的偶数。
1 <= Node.val <= 105

解题思路

1.我们先用快慢指针找到链表的中间节点，详细方法请参考【876.链表的中间节点】

2.然后我们将链表的后半部分反转，详细方法请参考【206.反转链表】

3.最后我们开始遍历原链表 head 和反转后的链表 reverse ，在两个链表同一位置的节点就是我们所要求的孪生节点，设置一个 sum 去计算孪生节点的值，再设置一个 max 与 sum 去比较将较大的值保存在 max 中，最后返回 max。

举个栗子：

（1）先调用mid（）函数找出中间节点

（2）再调用reverse（）函数反转后半部分链表

（3）设置一个 sum 去计算孪生节点的值，再设置一个 max 与 sum 去比较将较大的值保存在 max 中

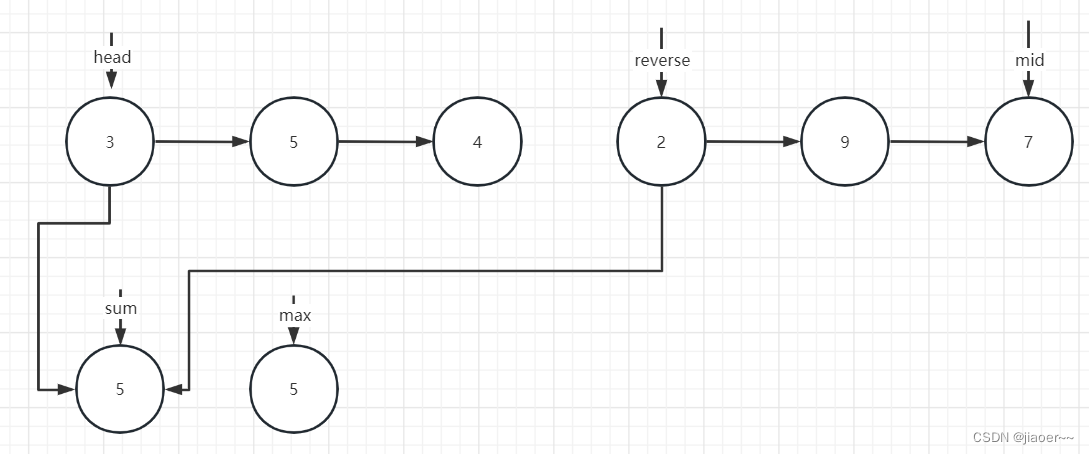
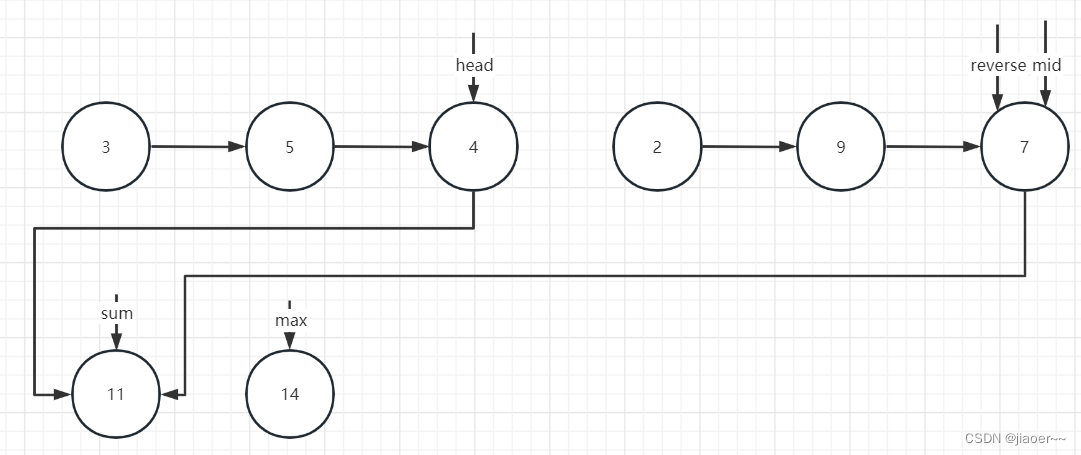
（4）此时 reverse 节点为空，返回 max 即可

代码实现

class Solution {
    public int pairSum(ListNode head) {
        ListNode mid = mid(head);
        ListNode reverse = reverse(mid);
        int max = 0;
        while(reverse != null){
            int sum = head.val + reverse.val;
            head = head.next;
            reverse = reverse.next;
            if(sum > max){
                max = sum;
            }
        }
    return max;
    }
     private ListNode mid(ListNode head){
        if(head == null || head.next == null){
            return head;
        }
        ListNode fast = head;
        ListNode slow = head;
        while(fast != null && fast.next != null){
            fast = fast.next.next;
            slow = slow.next;
        }
        return slow;
     }
      private ListNode reverse(ListNode head){
        ListNode per = null;
        ListNode cur = head;
        while(cur != null){
            ListNode curNext = cur.next;
            cur.next = per;
            per = cur;
            cur = curNext;
    }
             return per;
}
}