图源:文心一言
考研笔记整理6k+字,小白友好、代码可跑,请小伙伴放心食用~~🥝🥝
第1版:查资料、画导图、画配图~🧩🧩
参考用书:王道考研《2024年 数据结构考研复习指导》
参考用书配套视频:7.3_1 二叉排序树_哔哩哔哩_bilibili
特别感谢: Chat GPT老师、文心一言老师~
📇目录
📇目录
🦮思维导图
🧵基本概念
⏲️哈夫曼树简介
🌰构造举栗
⌨️代码实现
🧵分段代码
🔯P0:调用库文件
🔯P1:定义结点与指针
🔯P2:用于优先队列中的比较函数
🔯P3:构造哈夫曼树
🔯P4:打印哈夫曼树编码
🔯P5:计算哈夫曼树的权值路径长度(WPL)
🔯P6:main函数
🧵完整代码
🔯P0:完整代码
🔯P1:执行结果
🔚结语
🦮思维导图
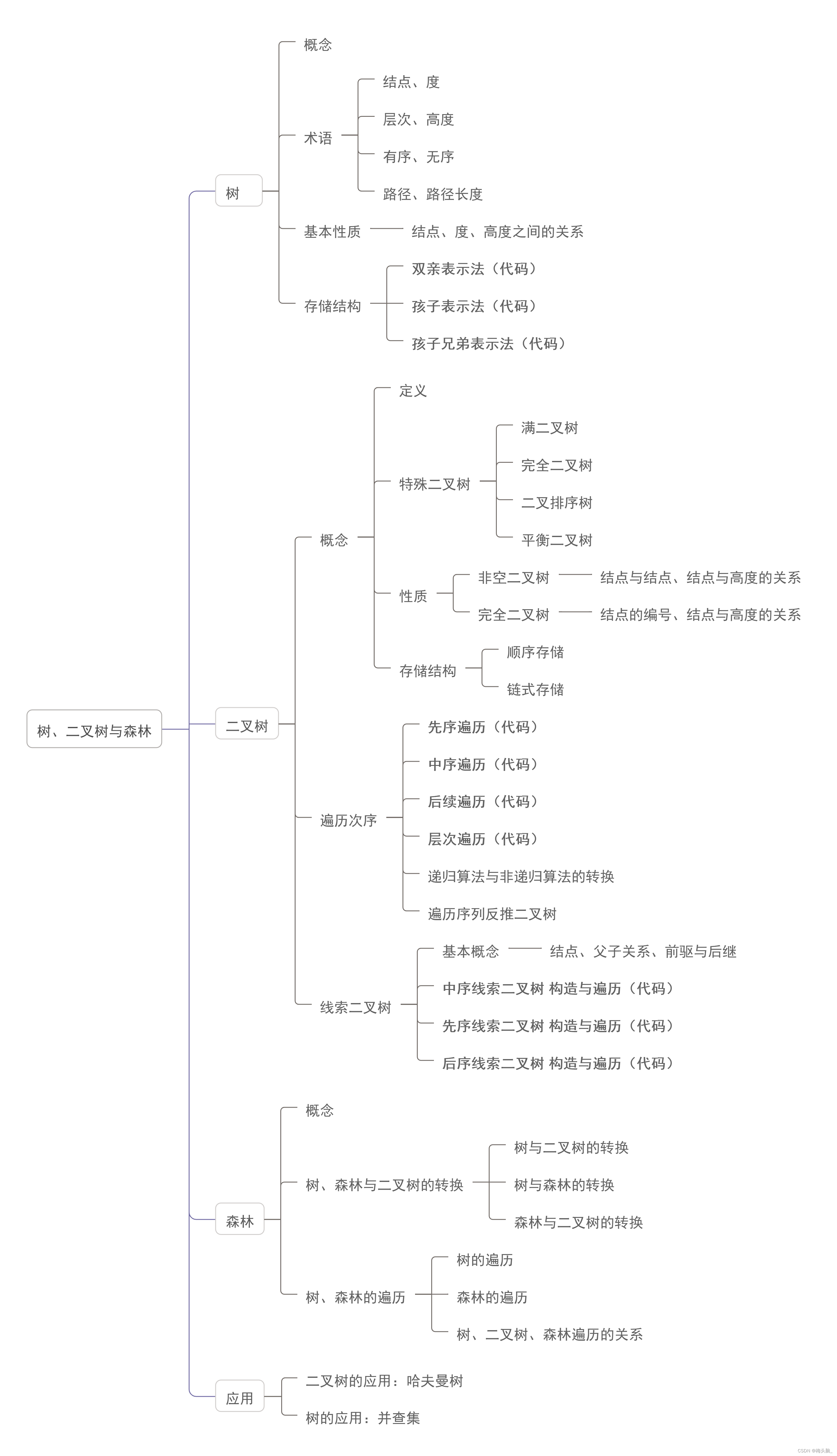
备注:
- 思维导图为整理王道教材第5章 查找的所有内容;
- 本篇仅涉及到哈夫曼树HuffmanTree的代码;
- 本章节往期博文,涉及到树与二叉树的内容如下~
- 🌸[树:双亲、孩子、兄弟表示法][二叉树:先序、中序、后序遍历]
- 🌸数据结构05:树与二叉树[C++][线索二叉树:先序、中序、后序]
🧵基本概念
⏲️哈夫曼树简介
哈夫曼树的起源:
哈夫曼树是由一位美国数学家David A. Huffman在1952年发明的,它的设计灵感来源于信息的编码与传输。在计算机科学中,我们经常需要将字符或数据编码为二进制形式以便传输和存储。哈夫曼树就是一种通过将出现频率高的字符赋予较短编码,从而实现高效编码的数据结构。
哈夫曼树的用途:
首先,哈夫曼树在数据压缩领域中被广泛应用。在我们的日常生活中,常常会遇到需要传输或存储大量数据的情况,比如发送电子邮件、观看在线视频等。而传输或存储数据需要消耗带宽或存储空间,因此我们希望尽可能减少数据的体积。
哈夫曼树通过根据字符的出现频率构建一种最优的编码方式,使得频率高的字符使用较短的二进制编码,而频率低的字符使用较长的二进制编码。这样一来,我们可以在不损失数据的情况下,显著减小数据的体积,从而实现高效的数据压缩,我们可以在网络传输中更高效地传输数据,提升通信的质量和速度。
🌰构造举栗
哈夫曼树是带权路径最小路径长度的二叉树。
带权路径的公式为 = 求和(结点的权值 x 路径长度)
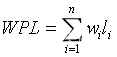
例如以下三棵树,结点均为“数据a(权值7)、数据b(权值5)、数据c(权值2)、数据d(权值4)”构成:
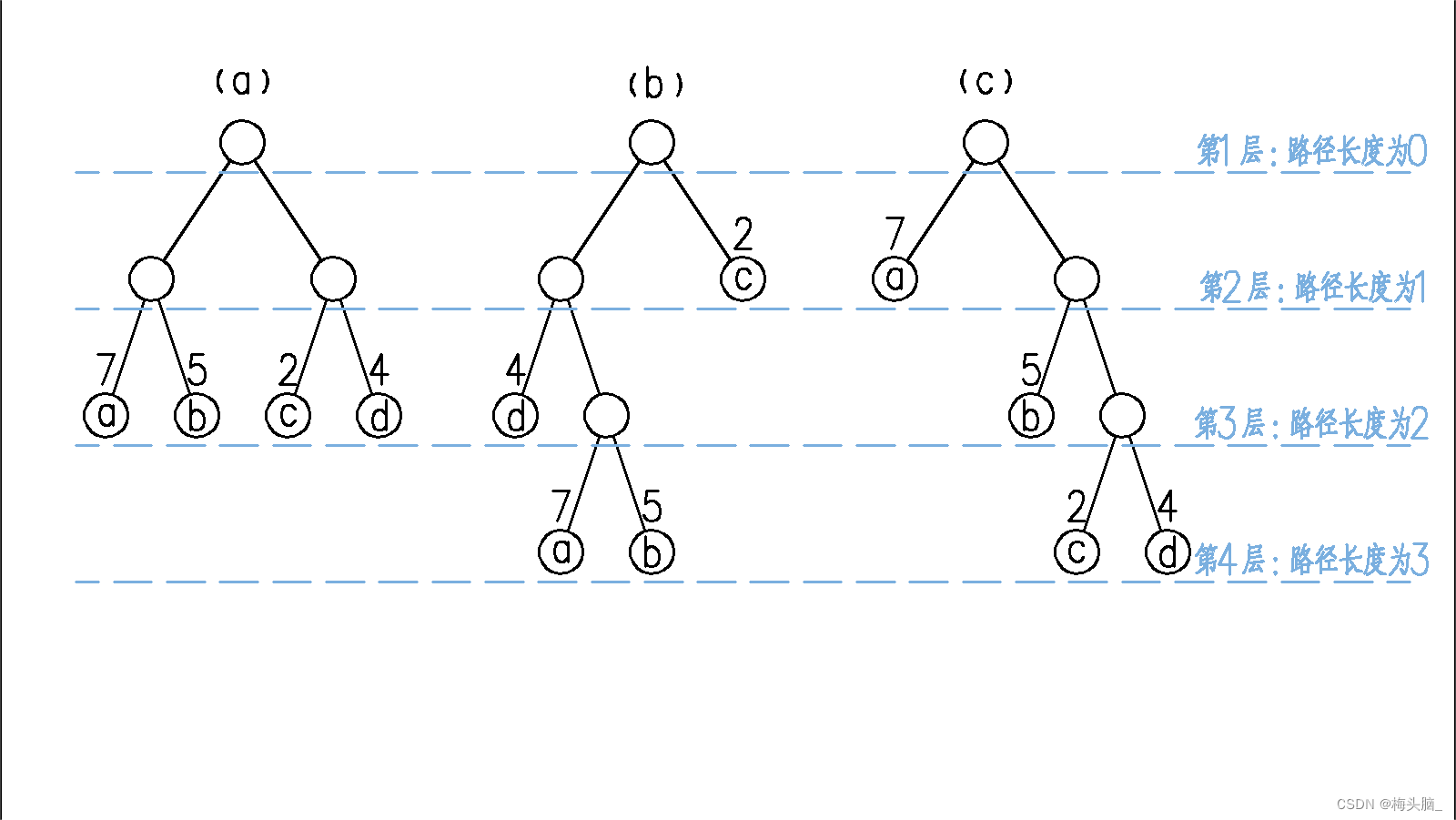
其构造方式不同,树的权值计算也有差异~
- 树a的WPL:(7+5+2+4)x2=36
- 树b的WPL:2x1+4x2+(7+5)x3=46
- 树c的WPL:7x1+5x2+(2+4)x3=35
这要怎么理解这棵树的含义呢?
例如在《天才枪手》中,我们需要利用时差蹲在厕所向队友传递一串选择题答案,这个答案包含“7个a、5个b、2个c、4个d”;并且约定短信内容一定要保密,防止被他人一眼偷窥到短信内容就是答案,我们约定“a、b、c、d”这4个选择由“0”和“1”这两个数字编码加密组成。
对应哈夫曼树,其左子树为0,右子树为1,那么:
- 树a的编码:a(00)、b(01)、c(10)、d(11),根据权值公式计算的结果,我们传递选择题答案需要在厕所偷偷摁36个数字;
- 树b的编码:a(010)、b(011)、c(1)、d(00),根据权值公式计算的结果,我们传递选择题答案需要在厕所偷偷摁46个数字;
- 树c的编码:a(0)、b(10)、c(110)、d(111),根据权值公式计算的结果,我们传递选择题答案需要在厕所偷偷摁35个数字;
这就体现出选择树c编码的好处了~如果不幸选择树b编码的话,会把答案出现频率最高a、b的答案排最长的编码010、011,真的要摁到手麻才能出门~
那如何构成树c呢?
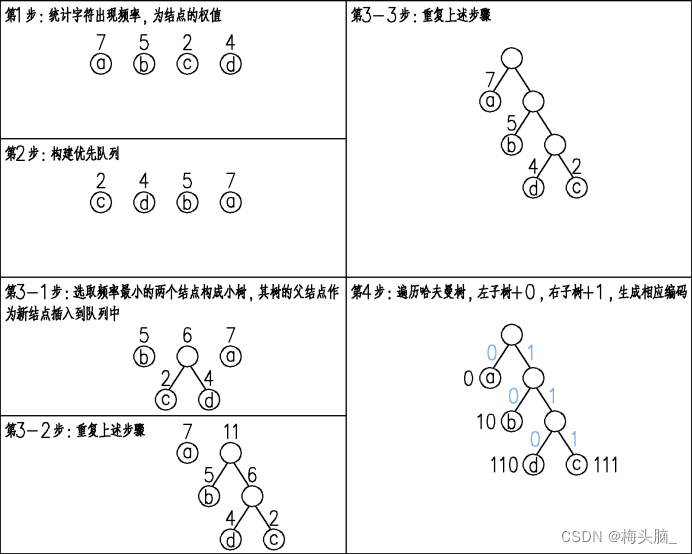
如上图,文字阐述具体步骤如下:
- 首先,我们需要统计字符的出现频率。这可以通过扫描待编码的数据来实现,统计每个字符出现的次数。
- 接下来,我们将统计得到的每个字符及其对应的频率作为叶节点,构建一个优先队列。
- 然后,我们从优先队列中选取频率最小的两个节点,创建一个新的节点作为它们的父节点,并将父节点插入到优先队列中。重复上述步骤,直到优先队列中只剩下一个节点,这个节点就是哈夫曼树的根节点。
- 最后,我们可以通过遍历哈夫曼树,为每个字符生成对应的编码。从根节点开始,左子树路径表示编码位"0",右子树路径表示编码位"1",直到达到叶节点。通过遍历路径,我们可以为每个字符生成唯一的哈夫曼编码。
下面我们以图中的小树为例,简单列出哈夫曼树的构造代码{这次的代码是GPT老师生成的}~

图源:文心一言
⌨️代码实现
🧵分段代码
🔯P0:调用库文件
- 输入输出流文件iostream{本代码用于输入与输出};
- 动态数组的向量文件vector{本代码用于比较队列中结点的大小};
- 队列函数文件queue{本代码用于创建哈夫曼树}~
#include <iostream>
#include <queue>
#include <vector>🔯P1:定义结点与指针
struct HuffmanNode {
char data; //定义字符
int frequency; //定义频率
HuffmanNode *left, *right; //定义左指针、右指针
HuffmanNode(char data, int frequency) { //初始化
this->data = data;
this->frequency = frequency;
left = right = nullptr;
}
};🔯P2:用于优先队列中的比较函数
创建结点的步骤在调整<优先队列>时重复出现,因此使用函数封装~
思路:比较指针指向的两个函数,权值高的结点优先度降低。
struct Compare {
bool operator()(HuffmanNode* a, HuffmanNode* b) { //接受两个HuffmanNode对象的指针作为参数,即HuffmanNode* a和HuffmanNode* b
return a->frequency > b->frequency; //判断a的频率是否大于b的频率,频率高的结点优先度更低
}
};🔯P3:构造哈夫曼树
传入main函数中的数据动态数组data和频度动态数组frequency~
本步骤的构建过程在博文上面已有图文解释,此处不再赘述~
HuffmanNode* buildHuffmanTree(const vector<char>& data, const vector<int>& frequency) {
priority_queue<HuffmanNode*, vector<HuffmanNode*>, Compare> pq; //声明了一个优先队列(priority_queue),其中存储的是HuffmanNode类型的对象指针。这个优先队列使用了一个比较函数(Compare)来定义元素的优先级
// 创建叶结点并将它们插入优先队列
for (int i = 0; i < data.size(); i++) {
pq.push(new HuffmanNode(data[i], frequency[i]));
}
// 构建哈夫曼树
while (pq.size() > 1) {
HuffmanNode* left = pq.top(); //队首元素记录并出列,即左子结点(left)
pq.pop();
HuffmanNode* right = pq.top(); //队首元素记录并出列,即右子结点(right)
pq.pop();
HuffmanNode* newNode = new HuffmanNode('$', left->frequency + right->frequency); //创建了一个新的HuffmanNode对象,它的频率是左子节点和右子节点的频率之和
newNode->left = left; //在树中链接新节点和左子结点
newNode->right = right; //在树中链接新节点和右子结点
pq.push(newNode); //将新的结点插回队列
}
return pq.top(); //返回根结点
}🔯P4:打印哈夫曼树编码
传入树的根结点内存地址,编码由空值开始,以左子树+0,右子树+1的方式遍历树中的结点,如果是叶结点则打印编码~
void printHuffmanCodes(HuffmanNode* root, string code) {
if (root == nullptr) {
return;
}
// 如果是叶结点,则打印字符和对应的编码
if (!root->left && !root->right) {
cout << root->data << " : " << code << endl;
}
// 递归打印左子树和右子树
printHuffmanCodes(root->left, code + "0");
printHuffmanCodes(root->right, code + "1");
}🔯P5:计算哈夫曼树的权值路径长度(WPL)
传入树的根结点内存地址,树高由0开始(根结点那一行不算权值),先序遍历树中的结点,如果遇到叶子结点则计算权值(频度x权值),并返回加和~
先序遍历的内容可以看这里:🌸[树:双亲、孩子、兄弟表示法][二叉树:先序、中序、后序遍历]
int calculateWPL(HuffmanNode* root, int depth) {
if (root == nullptr) {
return 0;
}
// 如果是叶结点,返回权值乘以深度
if (!root->left && !root->right) {
return root->frequency * depth;
}
// 递归计算左子树和右子树的WPL
int leftWPL = calculateWPL(root->left, depth + 1);
int rightWPL = calculateWPL(root->right, depth + 1);
return leftWPL + rightWPL;
}🔯P6:main函数
main函数除了P0~P5的函数调用,就创建了频度与结点值,以及示意性地增加了结果输出~
int main() {
// 示例数据
vector<char> data = {'A', 'B', 'C', 'D'};
vector<int> frequency = {7, 5, 2, 4};
// 构建哈夫曼树
HuffmanNode* root = buildHuffmanTree(data, frequency);
// 打印哈夫曼树的编码
cout << "Huffman Codes:" << endl;
printHuffmanCodes(root, "");
// 计算并打印哈夫曼树的权值路径长度(WPL)
int wpl = calculateWPL(root, 0);
cout << "Weighted Path Length (WPL): " << wpl << endl;
return 0;
}🧵完整代码
🔯P0:完整代码
为了凑本文的字数,我这里贴一下整体的代码,删掉了细部注释~
#include <iostream>
#include <queue>
#include <vector>
using namespace std;
// 哈夫曼树的结点定义
struct HuffmanNode {
char data;
int frequency;
HuffmanNode *left, *right;
HuffmanNode(char data, int frequency) {
this->data = data;
this->frequency = frequency;
left = right = nullptr;
}
};
// 用于优先队列中的比较函数
struct Compare {
bool operator()(HuffmanNode* a, HuffmanNode* b) {
return a->frequency > b->frequency;
}
};
// 生成哈夫曼树
HuffmanNode* buildHuffmanTree(const vector<char>& data, const vector<int>& frequency) {
priority_queue<HuffmanNode*, vector<HuffmanNode*>, Compare> pq;
for (int i = 0; i < data.size(); i++) {
pq.push(new HuffmanNode(data[i], frequency[i]));
}
while (pq.size() > 1) {
HuffmanNode* left = pq.top();
pq.pop();
HuffmanNode* right = pq.top();
pq.pop();
HuffmanNode* newNode = new HuffmanNode('$', left->frequency + right->frequency);
newNode->left = left;
newNode->right = right;
pq.push(newNode);
}
return pq.top();
}
// 打印哈夫曼树中的编码
void printHuffmanCodes(HuffmanNode* root, string code) {
if (root == nullptr) {
return;
}
if (!root->left && !root->right) {
cout << root->data << " : " << code << endl;
}
printHuffmanCodes(root->left, code + "0");
printHuffmanCodes(root->right, code + "1");
}
// 计算哈夫曼树的权值路径长度(WPL)
int calculateWPL(HuffmanNode* root, int depth) {
if (root == nullptr) {
return 0;
}
if (!root->left && !root->right) {
return root->frequency * depth;
}
int leftWPL = calculateWPL(root->left, depth + 1);
int rightWPL = calculateWPL(root->right, depth + 1);
return leftWPL + rightWPL;
}
int main() {
vector<char> data = {'A', 'B', 'C', 'D'};
vector<int> frequency = {7, 5, 2, 4};
HuffmanNode* root = buildHuffmanTree(data, frequency);
cout << "Huffman Codes:" << endl;
printHuffmanCodes(root, "");
int wpl = calculateWPL(root, 0);
cout << "Weighted Path Length (WPL): " << wpl << endl;
return 0;
}
🔯P1:执行结果
运行结果如下图所示~
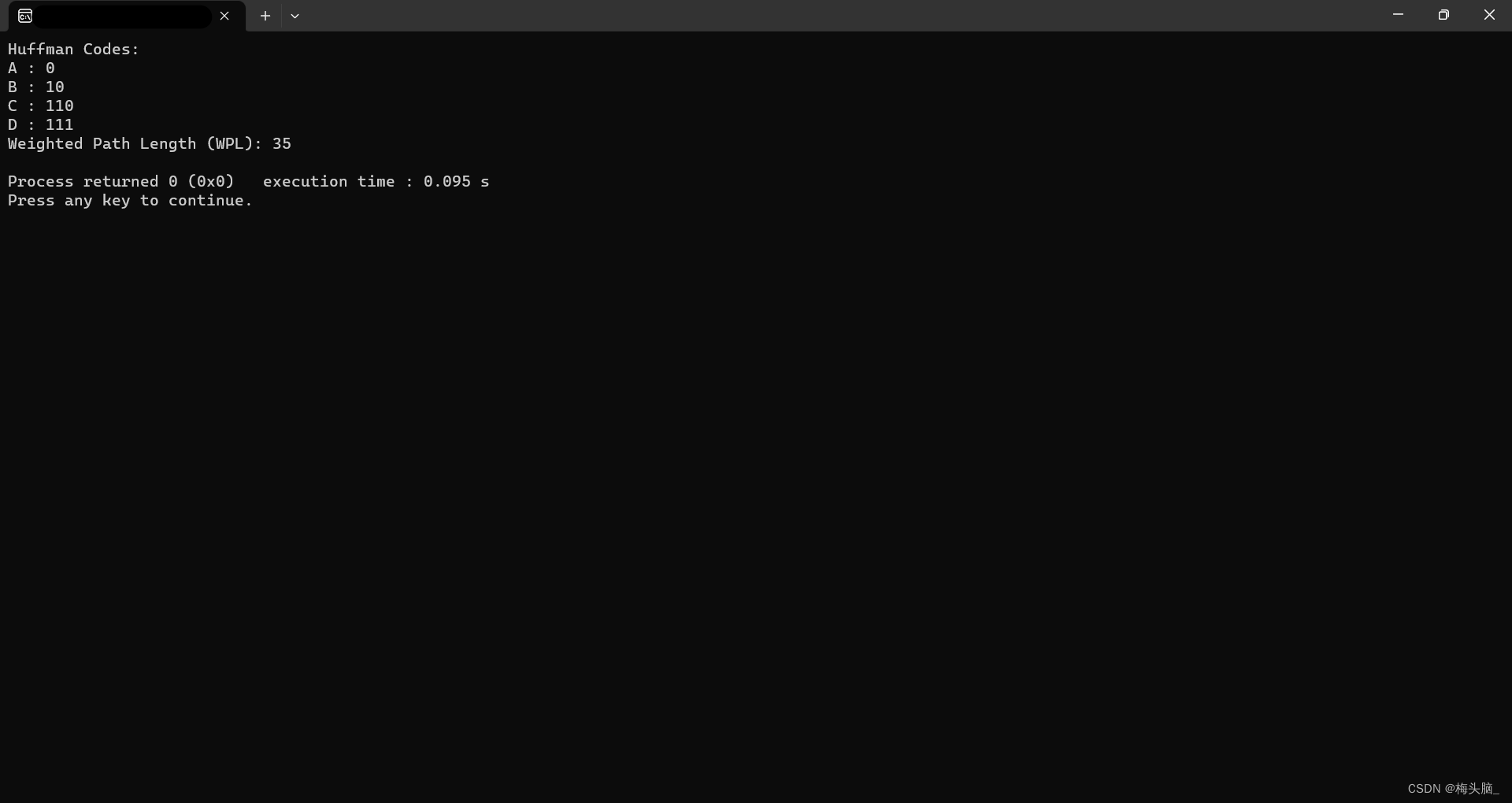
🔚结语
博文到此结束,写得模糊或者有误之处,欢迎小伙伴留言讨论与批评,督促博主优化内容,不限于以下内容~😶🌫️😶🌫️
- 有错误:这段注释南辕北辙,理解错误,需要更改~
- 难理解:这段代码雾里看花,需要更换排版、增加语法、逻辑注释或配图~
- 不简洁:这段代码瘠义肥辞,好像一座尸米山,需要更改逻辑;如果是C++语言,调用某库某语法还可以简化~
- 缺功能:这段代码败絮其中,能跑,然而不能用,想在实际运行或者通过考试需要增加功能~
- 跑不动:这不可能——好吧,如果真不能跑,告诉我哪里不能跑我再回去试试...
博文若有帮助,欢迎小伙伴动动可爱的小手默默给个赞支持一下~🌟🌟
有兴趣可以看看博主其它的博文,说不定会遇到感兴趣的内容~🌟🌟