第16章 母函数
母函数是离散数学领域最意外、最有用的发明之一。粗略来讲,母函数将序列问题转化为代数问题。
组合数学中常常出现普通型母函数、指数型母函数、狄利克雷型母函数
16.1 无穷级数
通俗地说,母函数F(x)就是无穷级数
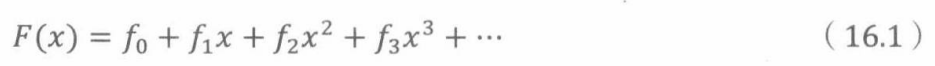
符号[ x n x^n xn]F(x)表示母函数F(x)中 x n x^n xn的系数,即[ x n x^n xn]F(x):= f n f_n fn。
将数列 f 0 , f 1 , . . . , f n f_0,f_1,..., f_n f0,f1,...,fn中的元素看成母函数的各项系数,分析这个数列的行为。我们发现,将序列看成母函数,很容易解释计数、递归定义以及程序设计中的复杂序列问题。
即便系数序列很简单,母函数也能够提供有价值的见解。例如,G(x)表示无穷序列1,1,…的母函数,即为几何级数。
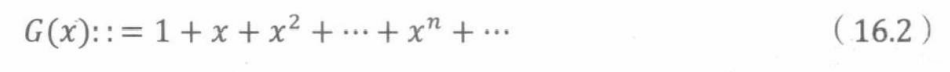
我们采用母函数推导G(x)的简化公式。

解得

即
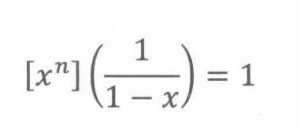
继续采用这个方法,可以得到以下漂亮的等式
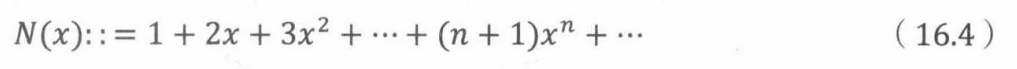
具体来说,即
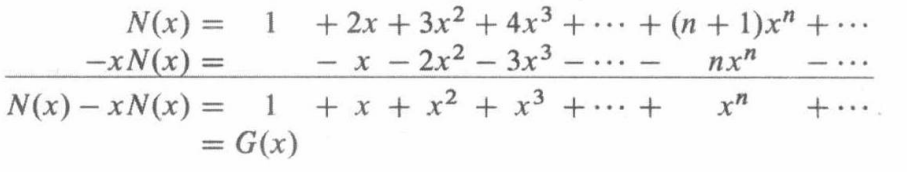
求解得
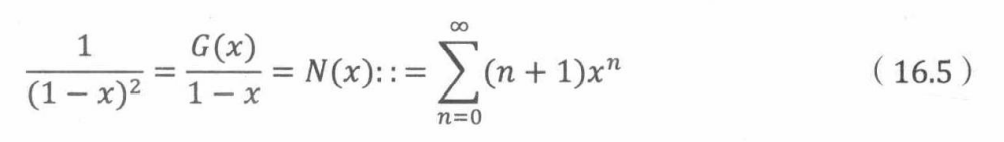
变形为
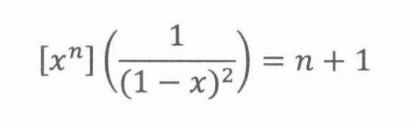
16.1.1 不收敛性
等式16.3和16.5仅当|x|<1时成立,因为它们的母函数在|x|≥1时发散。在母函数中,我们将无穷级数看作代数对象。诸如等式16.3和16.5定义的数理恒等式适用于纯代数理论。实际上,任意时候(x= 0处除外)都不收敛的无穷级数确定的母函数十分有用。我们将在本章最
16.2使用母函数计数
母函数尤其适用于表达和计算选择n个事物有多少种方法时。例如,假定有两种口味的甜甜圈,巧克力味和原味。设 d n d_n dn为挑选n个甜甜圈的方法个数,那么 d n d_n dn=n+1,即共有n+1种甜甜圈选择方法。于是我们定义一个母函数D(x)表示甜甜圈选择数,其中系数 x n x^n xn = d n d_n dn。可得

16.2.1 苹果和香蕉
假定我们有两件物品,比如苹果和香蕉,还有一些关于选择物品的约束条件。假设选择n个苹果共有 a n a_n an种选法,而选择n个香蕉共有 b n b_n bn种选法。那么对苹果计数的母函数就可以表示成
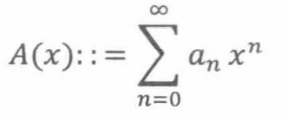
同理,香蕉对应的母函数则表示为
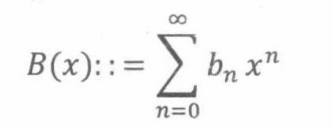
那么,苹果和香蕉混合在一起总共选择n个水果,有多少种选择呢?
n个苹果香蕉混合选择的数目等于
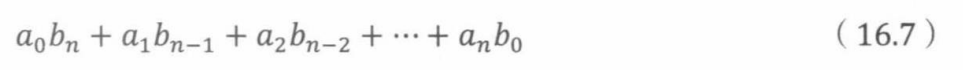
16.2.2 母函数的积
表达式16.7等于乘积A(x)B(x)中 x n x^n xn的系数。
法则(乘积)
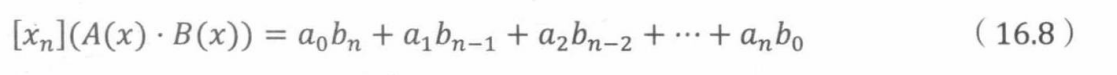
乘积A(x)·B(x)的系数序列称为序列( a 0 , a 1 , a 2 a_0,a_1,a_2 a0,a1,a2,.…)和( b 0 , b 1 , b 2 b_0,b_1,b_2 b0,b1,b2,…)的卷积。
乘积法则从代数上证明了无论是否收敛,几何级数都等于1/(1-x)这一事实。
特别地,常数1描述了如下母函数
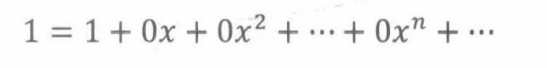
同理,1-x描述了以下母函数
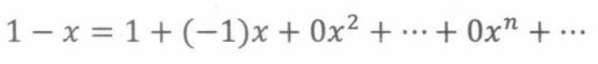
由乘积法则可得:
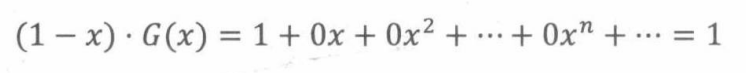
法则(常量):对于任一常量c和母函数F(x),都有

c = c x 0 + 0 x 1 + 0 x 2 + 0 x 3 + . . . . . . c = cx^0+0x^1+0x^2+0x^3+...... c=cx0+0x1+0x2+0x3+......
16.2.3 卷积法则
法则(卷积):令A(x)表示来自集合KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{A}的母函数,B(x)表示来自集合KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{B}的母函数,并且集合KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{A}与集合KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{B}不存在交集。故从并集KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{A} ∪ \cup ∪KaTeX parse error: Undefined control sequence: \cal at position 1: \̲c̲a̲l̲{B}中选择元素项构成的母函数即为乘积A(x)·B(x)。
16.2.4 利用卷积法则数甜甜圈
假设有两种巧克力和原味的甜甜圈可供选择。如果n个都选择巧克力,只有一种办法,母函数为1/(1-x)。同理,n个都选择原味,情况也一样。因此,根据卷积法则,从巧克力和原味两种口味的甜甜圈中选择n个甜甜圈,其选择方法数目的母函数为
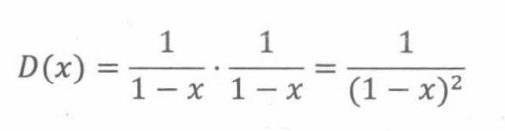
我们将利用卷积法则选择两种口味的问题推广至一般情况即选择k种口味。当有k种口味的甜甜圈可供选择时,相应的母函数为 1 / ( 1 一 x ) k 1/(1一x)^k 1/(1一x)k。我们推导出从k种口味的甜甜圈中选择n个,选择方法数对应的母函数。
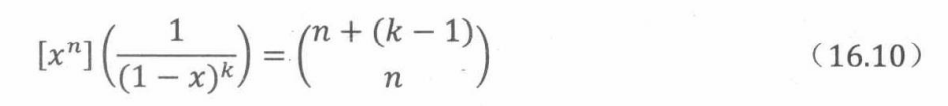
我们也可以用代数的方法去推导出 1 / ( 1 − x ) k 1/(1-x)^k 1/(1−x)k的系数
定理16.2.1(麦克劳林定理)
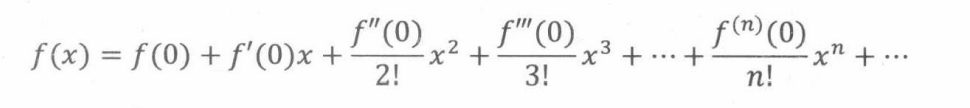
由以上的定理可以计算 1 / ( 1 − x ) k 1/(1-x)^k 1/(1−x)k的第n个系数
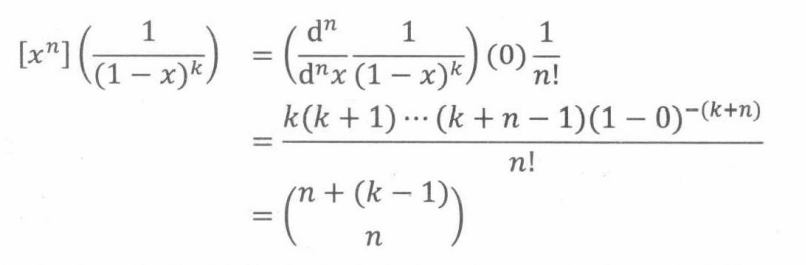
16.2.5 卷积法则中的二项式定理
首先考虑单元素集合{ a 1 a_1 a1}。从该集合选择n个不同的元素对应的母函数为1+x。根据卷积法则,从集合{ a 1 , a 2 , . . . , a m a_1, a_2,...,a_m a1,a2,...,am}选择一个n-元素子集对应的母函数,等于从这m个单元素集合分别选择元素的母函数的乘积 ( 1 + x ) m (1+x)^m (1+x)m。
从m个元素中选择n个元素的方法数为 ( m n ) \dbinom{m}{n} (nm),所以
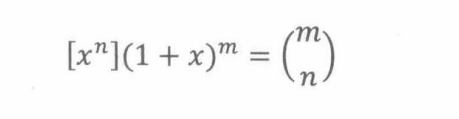
由此,我们可以看出母函数具有以下优势:
母函数能够通过代数手段解决计数问题,反之,使用计数技术同样也能够推导代数等式。
16.2.6一个荒唐的计数问题
在以下约束条件下,将袋子装满n个水果有多少种方式?

首先,构造一个选择苹果的母函数。
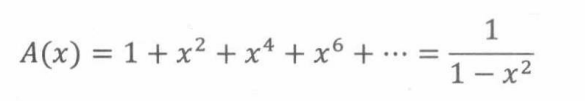
同理,选择香蕉的母函数是:
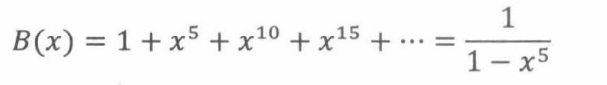
橘子的母函数为:
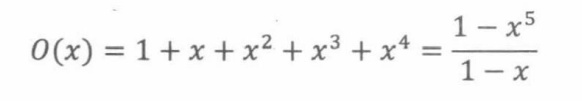
梨的母函数为:
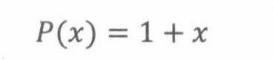
根据卷积法则,从这4类水果得出的母函数为:
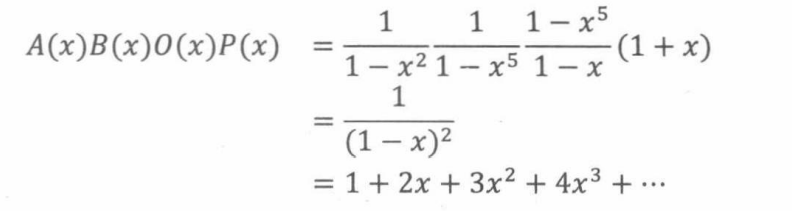
这个例子乍看起来很复杂,刚好说明了母函数解决计数问题的优势。
16.3 部分分式
在16.2.6小节中,我们最后把母函数化简成了 1 / ( 1 − x ) 2 1/(1-x)^2 1/(1−x)2,我们可以直接确定其幂级数的系数。但是对于其他一般性的问题,我们如何去求一个母函数幂级数的系数呢?
部分分式方法的基本思想是多项式的商能够表示为幂级数系数项之和。例如,当分母多项式存在不同的非零根,那么部分分式方法依赖于如下引理。
引理16.3.1:令P(x)表示小于n次的多项式, a 1 , . . . , a n a_1,...,a_n a1,...,an表示各不相等的非零数字,于是存在常量 c 1 , . . . , c n c_1,...,c_n c1,...,cn使得如下等式成立
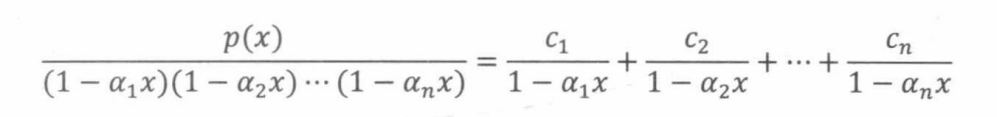
例子:
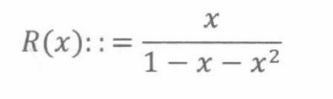
我们利用解二次方程的方法来确定分母 1 − x − x 2 1-x -x^2 1−x−x2的根 r 1 r_1 r1和 r 2 r_2 r2。
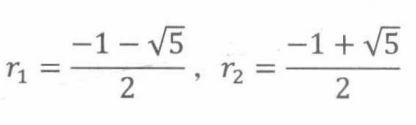
故
1 − x − x 2 = − ( x − r 1 ) ( x − r 2 ) = − r 1 r 2 ( 1 − x / r 1 ) ( 1 − x / r 2 ) 1-x-x^2 = -(x-r_1)(x-r_2) = -r_1r_2(1-x/r_1)(1-x/r_2) 1−x−x2=−(x−r1)(x−r2)=−r1r2(1−x/r1)(1−x/r2)
经过简单的代数处理,可得
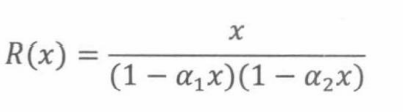
接下来我们确定常量c1,c2满足:
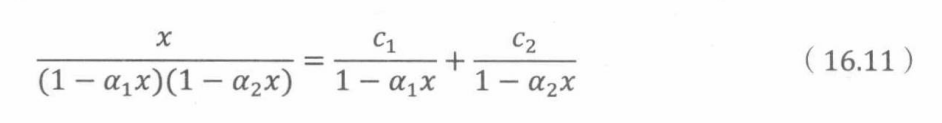
通过带值的方法可求 c 1 , c 2 c_1,c_2 c1,c2的值
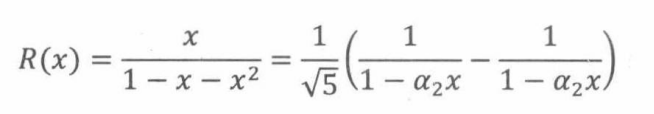
其中每一项都有一个简单的幂级数,其几何和公式为:
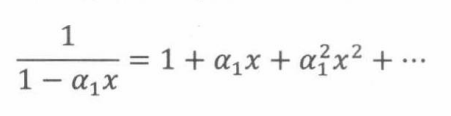
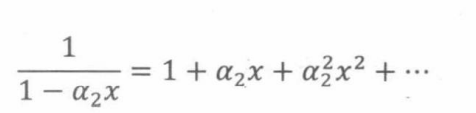
将以上幂级数代入母函数:
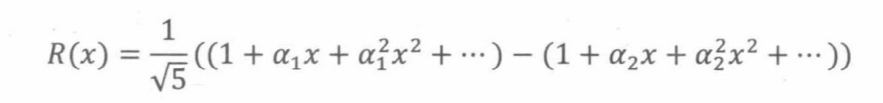
所以,
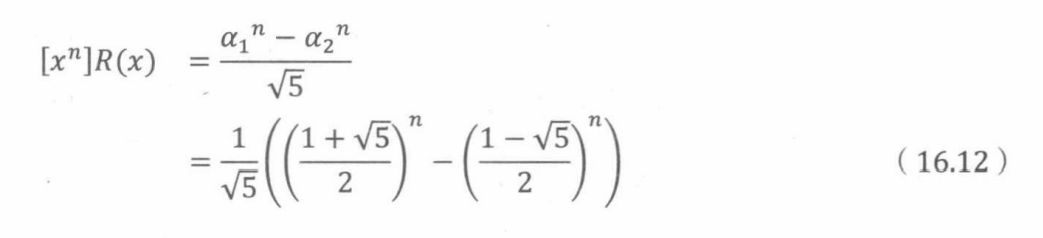
16.3.1 带有重根的部分分式
由引理16.3.1推导分母多项式存在带有m个非零重根的情况,即将商扩展为以下项的和

其中α是根的倒数且k≤m。这个项的系数公式符合“甜甜圈公式”(式16.10 ),即
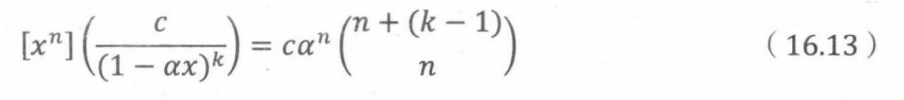
16.4求解线性递推
16.4.1斐波那契数的母函数
斐波那契数 f 0 , f 1 . . . . , f n , . . . f_0,f_1.... ,f_n,... f0,f1....,fn,...的递归定义如下:
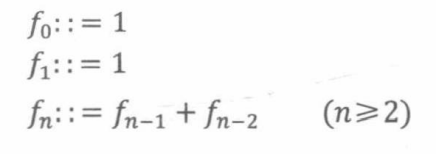
令F(x)为斐波那契数的母函数,即
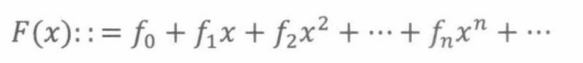
推导过程如下:
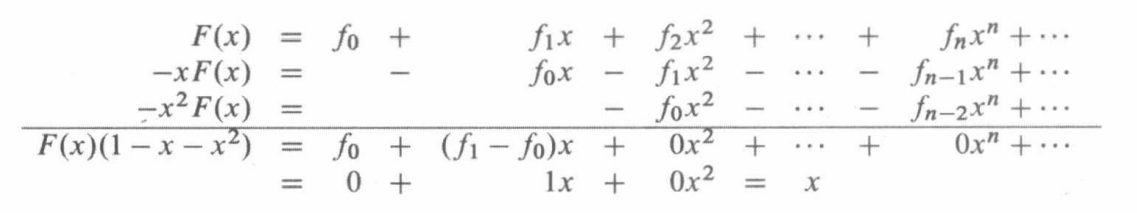
故:
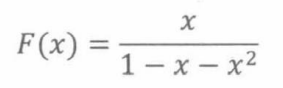
因此,以下公式叫做比内公式
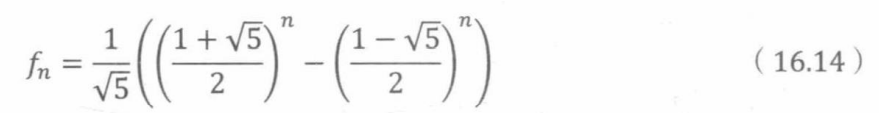
这个公式十分有用。例如,比内公式提供重复平方法计算斐波那契数,这比反复应用递推有效得多。此外,从比内公式可以明确看出斐波那契数呈指数级增长。
16.4.2 汉诺塔
相传,汉诺神庙有3根柱子和64个大小不同的金盘,每个盘子中间有一个洞可以套在柱子上。起初,64个盘子全部套在第一根柱子上,最小的盘子在顶端、最大的盘子在底端按顺序排放,如图16.1所示。
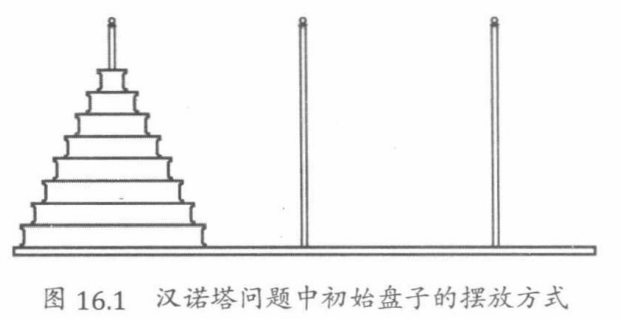
搬运规则如下:

递归方案:
经试验验证可知, t 1 = 1 , t 2 = 3 t_1= 1,t_2= 3 t1=1,t2=3。
递归过程有3个阶段,

**第一阶段:**将上方的n -1个盘子从第一根柱子移到第二根柱子,这个问题是n -1个盘子的移动问题。这一过程需要 t n − 1 t_{n-1} tn−1个步骤。
**第二阶段:**将最大的盘子从第一根柱子移到第三根柱子。这一过程仅需要1步就可完成。
**第三阶段:**将第二根柱子上的n - 1个盘子全部移到第三根柱子上。这一过程同样需要 t n − 1 t_{n-1} tn−1个步骤。
由此可知,递推公式为: t n = 2 t n − 1 + 1 t_n = 2t_{n-1}+1 tn=2tn−1+1
求解递推
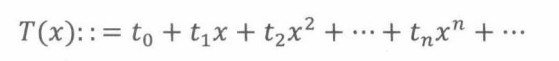
类似之前的斐波那契数递推推导,可得
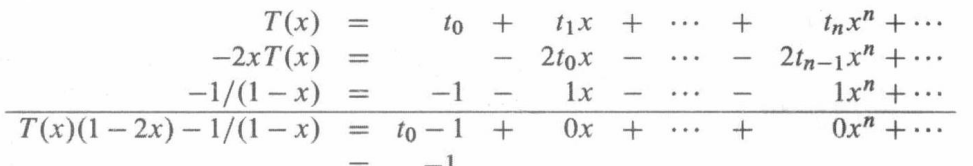
故

最后可求得:
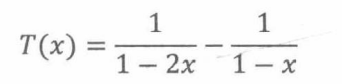
最后,我们可以得到移动n个盘子所需步数的简单公式:
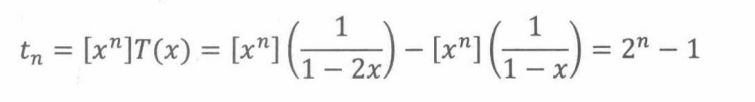
16.4.3 求解一般线性递推
形如

其中 c i c_i ci ∈ C,称为d阶线性非齐次递推方程,其中h(n)为非齐次项。
上述方法可以用来解决线性非齐次递推问题。
16.5 形式幂级数
16.5.1发散母函数
令F(x)为n!的母函数,即
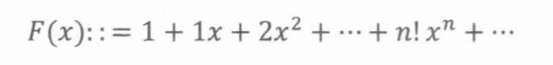
当x ≠ 0时F(x)发散,该母函数仅在x=0处收敛。
令H(x)为n ·n!的母函数,即
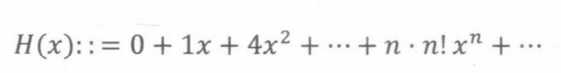
仅当x ≠ 0时H(x)发散。
什么是形式幂级数:
形式幂级数是一个数学中的抽象概念,是从幂级数中抽离出来的代数对象。不像幂级数一般要求研究是否收敛和是否有确定的取值。感兴趣的是系数序列。
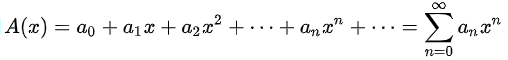
形如A(x)的幂级数,我们称以x为未定元的一个形式幂级数。
16.5.2幂级数环

我们仅考虑系数序列,假设:
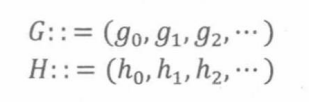
定义系列的和、序列相乘如下
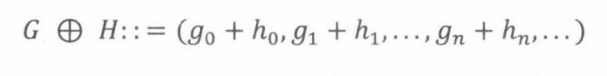
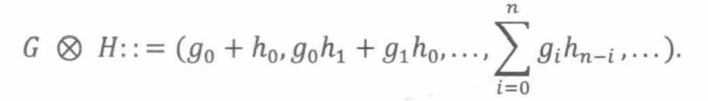
我们很容易证明他们满足交换律、结合律、分配律等
定义加法和乘法的单位元:

定义加法的逆元
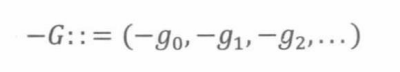
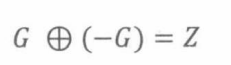
实际上,加法和乘法操作满足9.7.1节介绍的交换环公理。支持这种操作的无穷数列集合称为形式幂级数环。
如果:
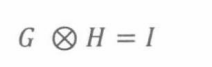
那么数列H是数列G的倒数列。则 G = 1 / H G = 1/H G=1/H、 H = 1 / G H = 1/G H=1/G。
现在我们换一种方式解释母函数
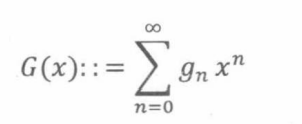
简单来说,G(x)就是形式幂级数环中系数 ( g 0 , g 1 , . . . ) (g_0,g_1,...) (g0,g1,...)构成的无穷数列。







![[附源码]计算机毕业设计大学生志愿者服务管理系统Springboot程序](https://img-blog.csdnimg.cn/40e3c265d5bf44af92f378b17e977ea8.png)

![[附源码]Python计算机毕业设计SSM基于微信平台的车险投保系统设计与实现(程序+LW)](https://img-blog.csdnimg.cn/9e1fcb8dd4df4505a4333c9a1d741b44.png)