代码随想录刷题记录 day38 最后一块石头的重量+目标和+1和0
参考:代码随想录
1049. 最后一块石头的重量 II
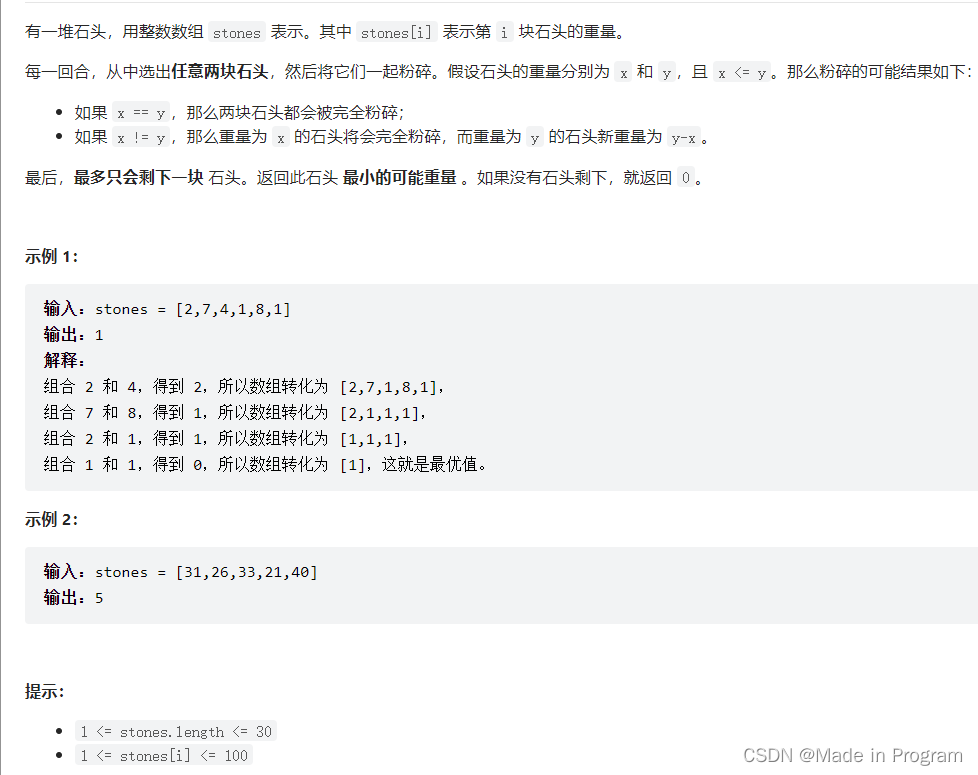
思想
把数组的石头尽可能地分成大小相等地两个集合
即sum/2;
容量为sum/2地背包尽可能地装满石头。
代码
class Solution {
public int lastStoneWeightII(int[] stones) {
//1.dp数组的定义
//dp[j] 表示容量为j的背包能装的最大的重量
//2.递推公式
//dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
//3.初始化
int [] dp=new int[1501];
int sum=0;
for(int stone:stones){
sum+=stone;
}
//4.遍历顺序
for(int i=0;i<stones.length;i++){
//先遍历物品
for(int j=sum/2;j>=stones[i];j--){
dp[j]=Math.max(dp[j],dp[j-stones[i]]+stones[i]);
}
}
return sum-dp[sum/2]-dp[sum/2];
}
}
494. 目标和
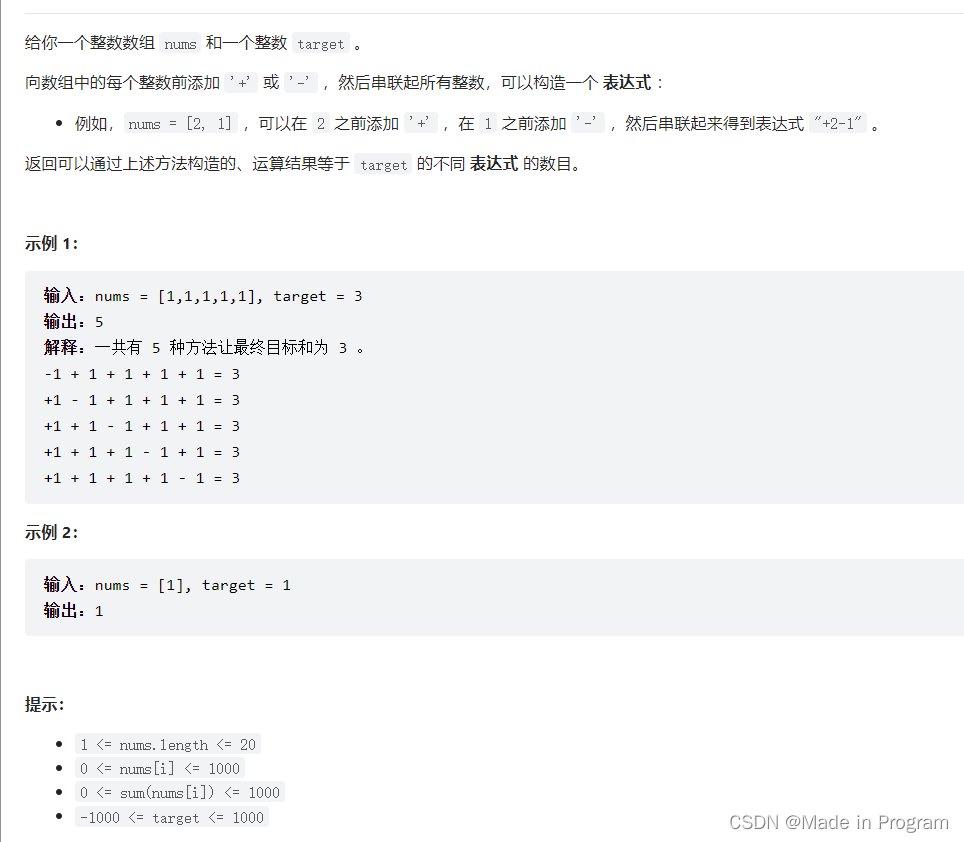
思想
加号或者减号 使之成为target
分解成两个集合,一个集合里面的数放加法,另外一个集合的数放减法
加法集合中的总和-减法集合中的总和: left-right=target; left+right=sum
由以上两个等式可得 left=(sum+target)/2 即加法集合中的和
此时就转换为 0 1背包问题,把容量为left的背包装满,有多少种方法
1.dp数组的定义
dp[j]表示 把容量为j的背包装满有dp[j]种不同的方法
dp[0]表示 把容量为1的背包装满有dp[0]种方法
dp[1]表示 把容量为1的背包装满有dp[1]种方法
dp[2]表示 把容量为1的背包装满有dp[2]种方法
dp[5]=1+dp[4]
如果j=5,即背包的容量等于5
当nums[i]=1时,有dp[4]种方法装备容量为5的背包
当nums[i]=2时,有dp[3]种方法装备容量为5的背包
当nums[i]=3时,有dp[2]种方法装备容量为5的背包
当nums[i]=4时,有dp[1]种方法装备容量为5的背包
当nums[i]=5时,有dp[0]种方法装备容量为5的背包
2.可得递推公式
可得dp[j] += dp[j - nums[i]]
3.初始化:主要考虑dp[0]
如果nums为[0] target=0,left=(sum+target)/2=0;
dp[0]=1,表示给数组里的元素 0 前面无论放加法还是减法,都是1种方法。
4.遍历顺序 0 1背包的遍历顺序
代码
class Solution {
public int findTargetSumWays(int[] nums, int target) {
// 加号或者减号 使之成为target
// 分解成两个集合,一个集合里面的数放加法,另外一个集合的数放减法
// 加法集合中的总和-减法集合中的总和: left-right=target; left+right=sum
// 由以上两个等式可得 left=(sum+target)/2 即加法集合中的和
// 此时就转换为 0 1背包问题,把容量为left的背包装满,有多少种方法
// 1.dp数组的定义
// dp[j]表示 把容量为j的背包装满有dp[j]种不同的方法
// dp[0]表示 把容量为1的背包装满有dp[0]种方法
// dp[1]表示 把容量为1的背包装满有dp[1]种方法
// dp[2]表示 把容量为1的背包装满有dp[2]种方法
// dp[5]=1+dp[4]
// 如果j=5,即背包的容量等于5
// 当nums[i]=1时,有dp[4]种方法装备容量为5的背包
// 当nums[i]=2时,有dp[3]种方法装备容量为5的背包
// 当nums[i]=3时,有dp[2]种方法装备容量为5的背包
// 当nums[i]=4时,有dp[1]种方法装备容量为5的背包
// 当nums[i]=5时,有dp[0]种方法装备容量为5的背包
// 2.可得递推公式
// 可得dp[j] += dp[j - nums[i]]
// 3.初始化:主要考虑dp[0]
// 如果nums为[0] target=0,left=(sum+target)/2=0;
// dp[0]=1,表示给数组里的元素 0 前面无论放加法还是减法,都是1种方法。
// 4.遍历顺序 0 1背包的遍历顺序
int sum=0;
for(int num:nums){
sum+=num;
}
if(sum<Math.abs(target)) return 0;
if((sum+target)%2==1) return 0;
int left=(sum+target)/2;
int[] dp=new int[left+1];
dp[0]=1;
for(int i=0;i<nums.length;i++){
for(int j=left;j>=nums[i];j--){
dp[j]+= dp[j - nums[i]];
}
}
for(int i=0;i<nums.length;i++){
//System.out.println(nums[i]);
}
return dp[left];
}
}
474. 一和零
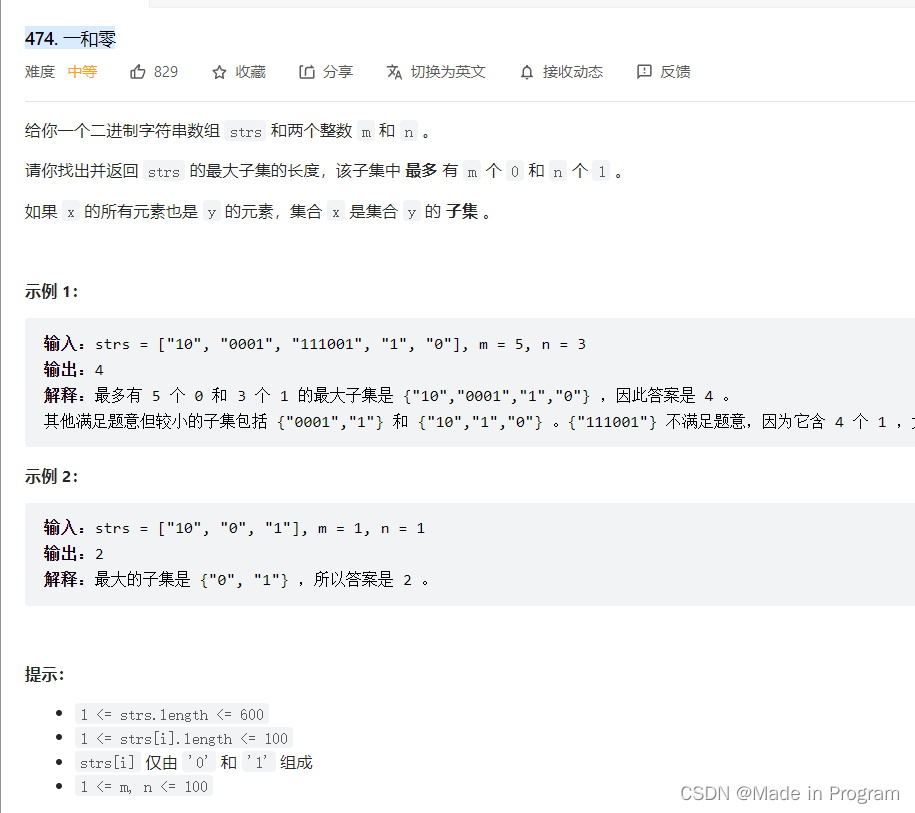
思想
转换成0 1 背包问题 这个背包有两个维度 m个0和n个1 ,物品就是数组中的元素string
1.dp[i][j]表示 容量为i个0和j个1的背包 能装的最大的子集
2.递推公式
dp[j]=Math.max(dp[j],dp[j-weight[i]]+values[i])
此题:若x表示当前物品0的个数,y表示当前物品1的个数
dp[i][j]=Math.max(dp[i][j],dp[i-x][j-y]+1)
dp[i-x][j-y]+1 表示加了当前这个元素
3.初始化
dp[0][0]=0,因为设涉及到取最大 所以其他的也初始化成0
4.遍历顺序 就是先遍历物品再遍历背包,背包倒序遍历
代码
class Solution {
public int findMaxForm(String[] strs, int m, int n) {
// 转换成0 1 背包问题 这个背包有两个维度 m个0和n个1 ,物品就是数组中的元素string
// 1.dp[i][j]表示 容量为i个0和j个1的背包 能装的最大的子集
// 2.递推公式
// dp[j]=Math.max(dp[j],dp[j-weight[i]]+values[i])
// 此题:若x表示当前物品0的个数,y表示当前物品1的个数
// dp[i][j]=Math.max(dp[i][j],dp[i-x][j-y]+1)
// dp[i-x][j-y]+1 表示加了当前这个元素
// 3.初始化
// dp[0][0]=0,因为设涉及到取最大 所以其他的也初始化成0
int [][] dp=new int[m+1][n+1];
dp[0][0]=0;
for(String str:strs){
//求得当前String 中包含0 和1的个数
int x=0,y=0;
for(int k=0;k<str.length();k++){
if(str.charAt(k)=='0')x++;
else y++;
}
//遍历顺序
for(int i=m;i>=x;i--){
for(int j=n;j>=y;j--){
dp[i][j]=Math.max(dp[i][j],dp[i-x][j-y]+1);
}
}
}
return dp[m][n];
}
}