【工业控制】多变量动态矩阵预测控制(DMC)【含Matlab源码 1499期】

news2024/11/16 6:44:18

⛄一、简介（附课程报告）

1引言
众所周知，上世纪 60 年代初形成的现代控制理论在航空、航天等领域取得了辉煌的成果。然而人们不久就发现在完美的理论与控制之间还存在着巨大的鸿沟。主要表现在以下几个方面:
1.现代控制理论的基点是对象精确的数学模型，而在工业过程中所涉及的对象往往是多输入、多输出的高维复杂系统其数学模型很难精确建立，即使建立了模型从工程应用的角度来说往往需要简化从而很难保证对象精确的模型。
2.工业对象的结构、参数和环境都有很大的不确定性。由于这些不确定性的存在按照理想模型得到的最优控制在实际上往往不能保证最优有时甚至引起控制品质的严重下降。在工业环境中人们更关注的是控制系统在不确定性影响下保持良好性能的能力即所谓鲁棒性而不能只是追求理想的最优性。
3.工业控制中必须考虑到控制手段的经济性。对工业计算机的要求不能太高. 因此控制算法必须简易以满足实时性的要求.而现代控制理论的许多算法往往过于复杂难以用低性能的计算机实现。
为了克服理论与实际应用之间的不协调，预测控制就是在这种背景下发展起来的。动态矩阵控制 DMC 是一种基于计算机控制的技术，它是一种增量算法，并基于系统的阶跃响应。它直接以对象的阶跃响应离散系数为模型，采用多步预估技术，能有效解决时延过程问题。按使预估输出与给定值偏差最小的二次性能指标实施控制。
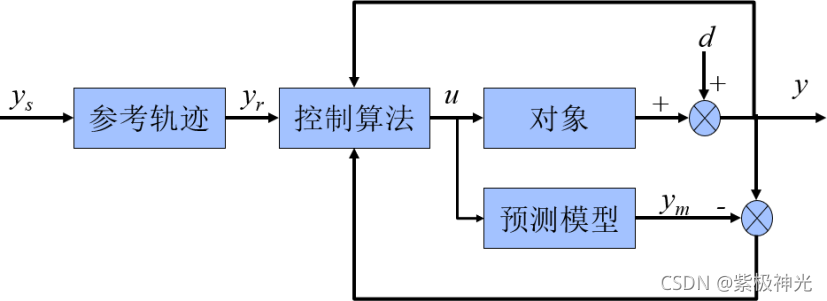
在这里插入图片描述
图 1 DMC 算法的控制结构
2 多变量 DMC 原理分析
DMC算法分为三部分:预测模型、滚动优化和反馈校正。
设被控对象有 m 个控制输入，p 个输出，假定已测得每一输出𝑦𝑖对每一输入
𝑢𝑗的单位阶跃相应𝑎𝑖𝑗(𝑡),则可由阶跃响应都在采样点上的值组成模型向量
在这里插入图片描述

⛄二、部分源代码

clear;clc;
num={[5],[3];[6],[9]};
den={[3 1 3],[1 2 5];[2 1 7],[2 3 6]};
sys=tf(num,den);%模型传递函数
g11=poly2tfd(num{1,1},den{1,1},0,0);
g12=poly2tfd(num{1,2},den{1,2},0,0);
g21=poly2tfd(num{2,1},den{2,1},0,0);
g22=poly2tfd(num{2,2},den{2,2},0,0);
delta=0.5;%采样时间
P=12;M=6;m=2;p=2;N=40; % M,P,m,p分别为控制时域长度，预测时域长度，输入量个数，输出量个数，N为建模时域
ny=2;
tfinal=500;
mymodel=tfd2step(tfinal,delta,ny,g11,g12,g21,g22);%计算阶跃响应模型

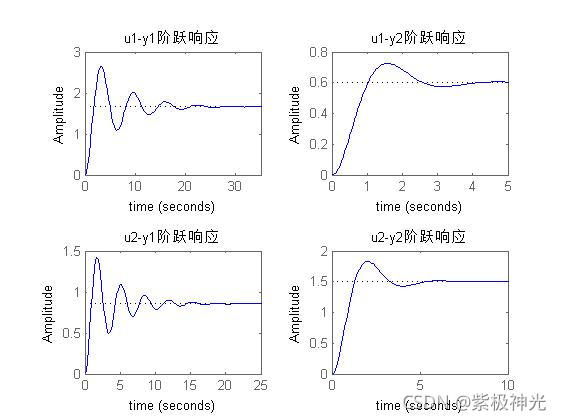
%作图，画出模型的阶跃响应曲线
figure(1)
subplot(2,2,1);
step(num{1,1},den{1,1});
title(‘u1-y1阶跃响应’);
xlabel(‘time’);
subplot(2,2,2);
step(num{1,2},den{1,2});
title(‘u1-y2阶跃响应’);
xlabel(‘time’);
subplot(2,2,3);
step(num{2,1},den{2,1});
title(‘u2-y1阶跃响应’);
xlabel(‘time’);
subplot(2,2,4);
step(num{2,2},den{2,2});
title(‘u2-y2阶跃响应’);
xlabel(‘time’);

ywt=[3,1];%Q矩阵
uwt=[400,300];%R矩阵
alpha=[1,1];%H矩阵
r=[1;2];%设定值
tend=500;%结束时间

%计算反馈校正H矩阵
H=[];
for i=1:p
h=alpha(1,i)*ones(N,1);
H=blkdiag(H,h);
end

%计算移位矩阵S
for i=1:p
for j=1:N-1
S((i-1)N+j,(i-1)N+j+1)=1;%次对角线元素为1
end
S((iN),(iN))=1;%右下角元素为1
end

%输出设定值R矩阵
R=[];
for i=1:p
r=r(i,1)*ones(P,1);
R=[R;r];
end

for i=1:p
for j=1:N
y_N((i-1)*N+j,1)=0;
y_N0((i-1)*N+j,1)=0;
end
for j=1:P
y_P0((i-1)*P+j,1)=0;
end
end
deltY=[];
deltU=[];
y_Ncor=[];

[kmpc,A,L,A_N,a,Q]=DMC_martixD(mymodel,uwt,ywt,M,P,m,p,N);%计算D矩阵

for i=1:1:tend
e(:,i)=y_Real(:,i)-y(:,i);
y_Ncor(:,i)=y_N(:,i)+He(:,i);
y_N0(:,i)=Sy_Ncor(:,i);

deltY(:,i)=R-y_P0(:,i);
deltU(:,i)=kmpc*(R-y_P0(:,i));
U(:,i+1)=deltU(:,i)+U(:,i);
y_N(:,i+1)=y_N0(:,i)+A_N*deltU(:,i);
for j=1:p
    y(j,i+1)=y_N((j-1)*N+1,i+1);
end
t=0:delta:delta*i;
 y_Real1=lsim(sys(:,1),U(1,1:i+1),t)+lsim(sys(:,2),U(2,1:i+1),t);
 y_Real=y_Real1';

end

n=size(y_Real(1,:));
n=n(1,2);
t=1:1:n;

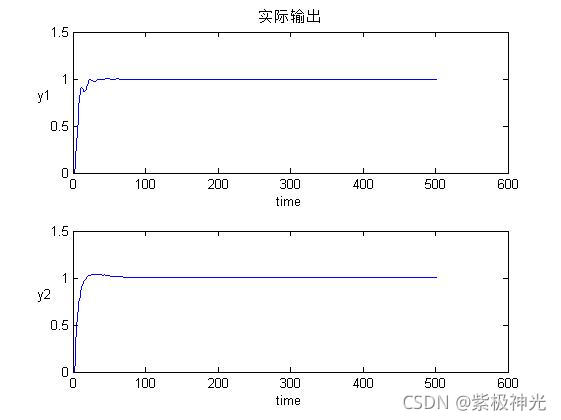
figure(2);
subplot(2,1,1);
plot(t,y_Real(1,1:n));
title(‘实际输出’);
ylabel(‘y1’,‘rotation’,0);xlabel(‘time’);

subplot(2,1,2);
plot(t,y_Real(2,1:n));
ylabel(‘y2’,‘rotation’,0);xlabel(‘time’);