x.1 feature scale

接下俩我们将考虑数据的不一致性，例如有的数据的范围很大，可能分布在好几千，但是我们的weight矩阵最好是在[-1, 1]的小数，如果数值太大就会导致我们的weight变化也很大，如下面这个例子就并不好，

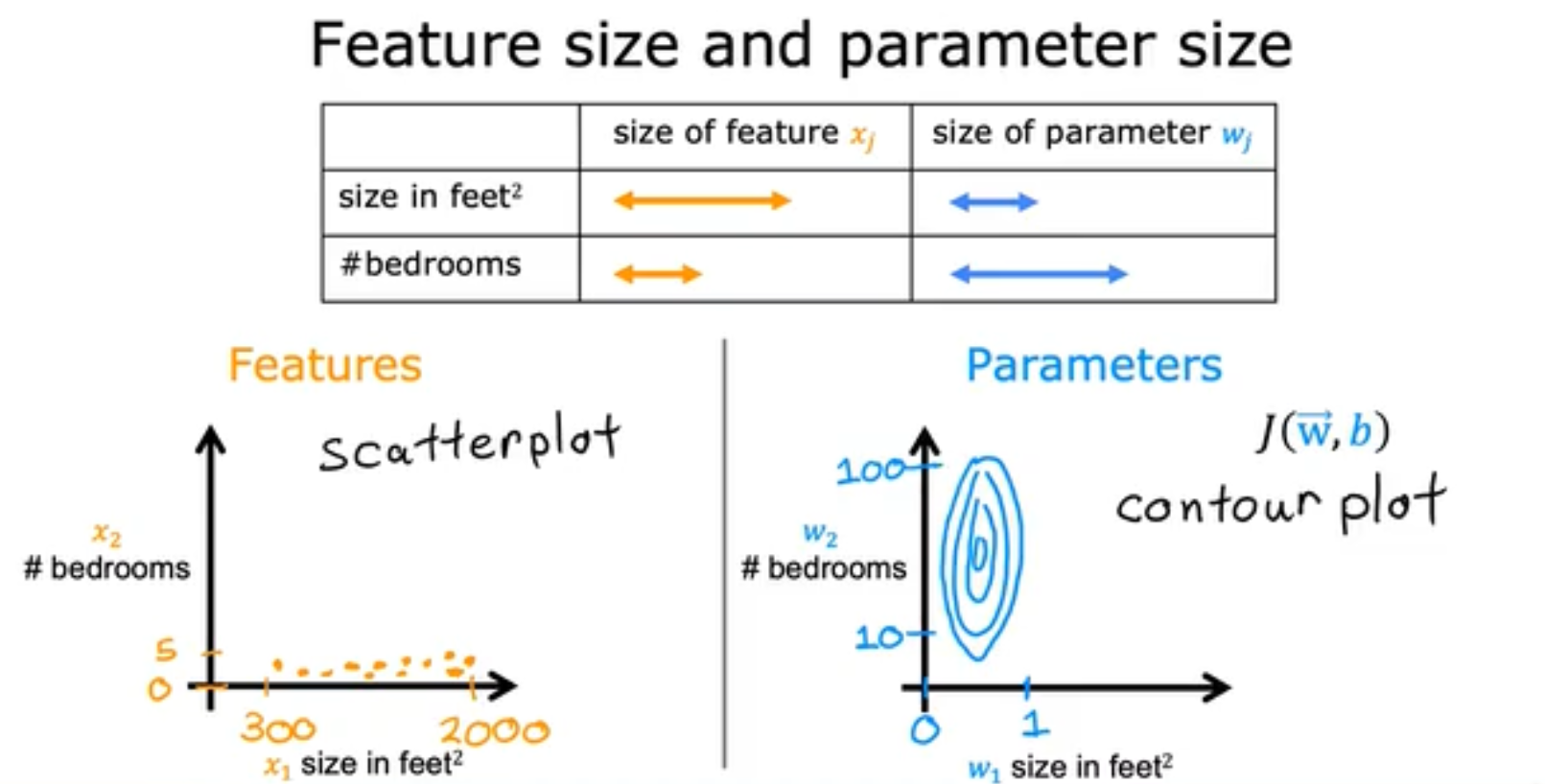
那么feature特征的大小对于parameters参数的大小究竟有什么关系呢，我们使用如下这个例子。我们能够观察到如果两个不同的Feature的size相差太大，会导致parameters的椭圆最终呈现及其细长的样子，这样并不容易收敛，

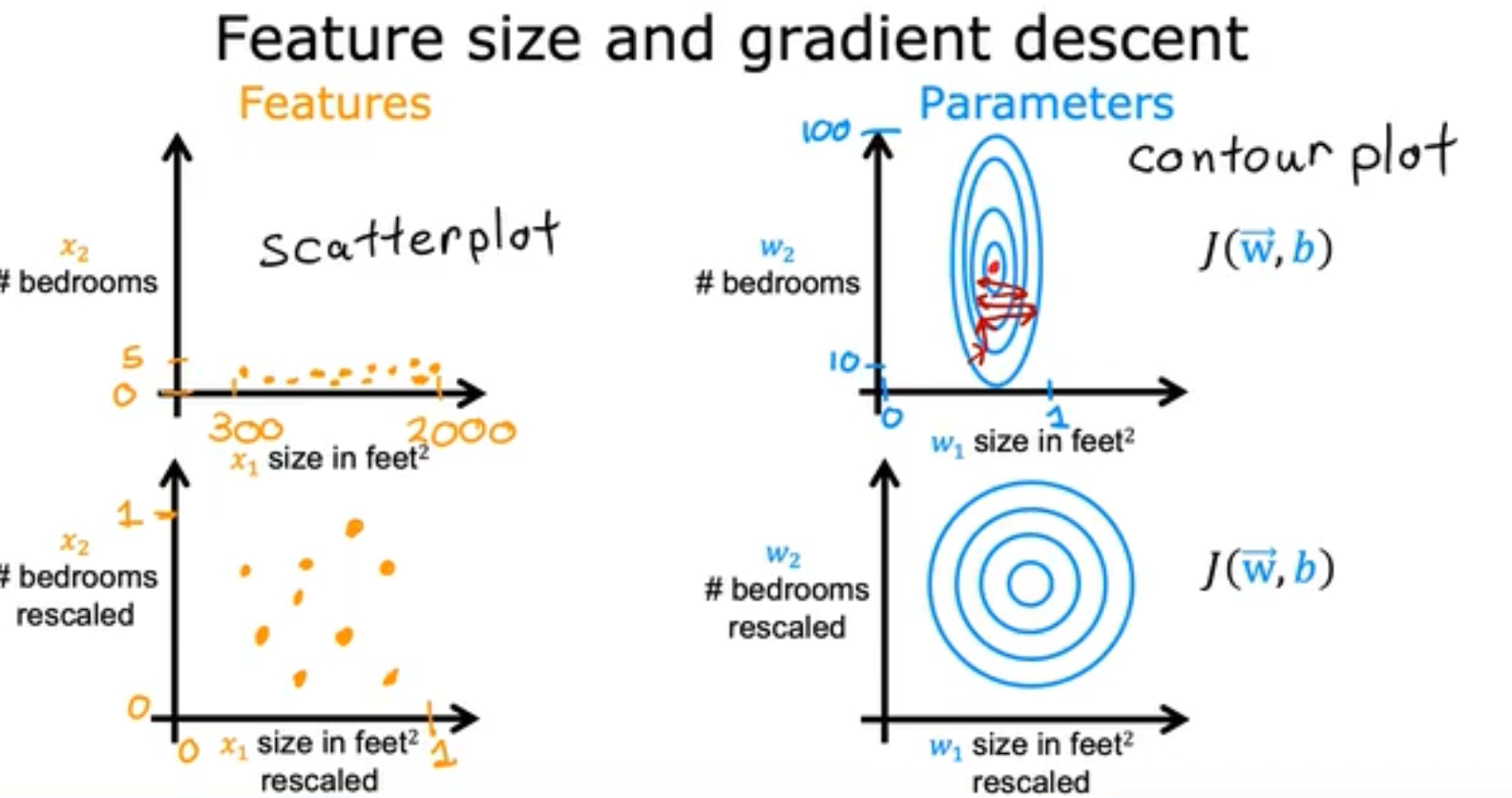
如果两个feature的数据没有进行归一化，则他们之间的数据大小会反复回弹，但是当进行归一化后gradient descent的图就成了多个同心圆，也就更容易收敛，

但是如果对数据进行feature scale特征缩放呢，具有多种方法，例如，

• Feature scaling：将特征除以最大值
• Mean normalization：减去均值除以极差
• Z-score normalization：标准化。减去均值除以标准差

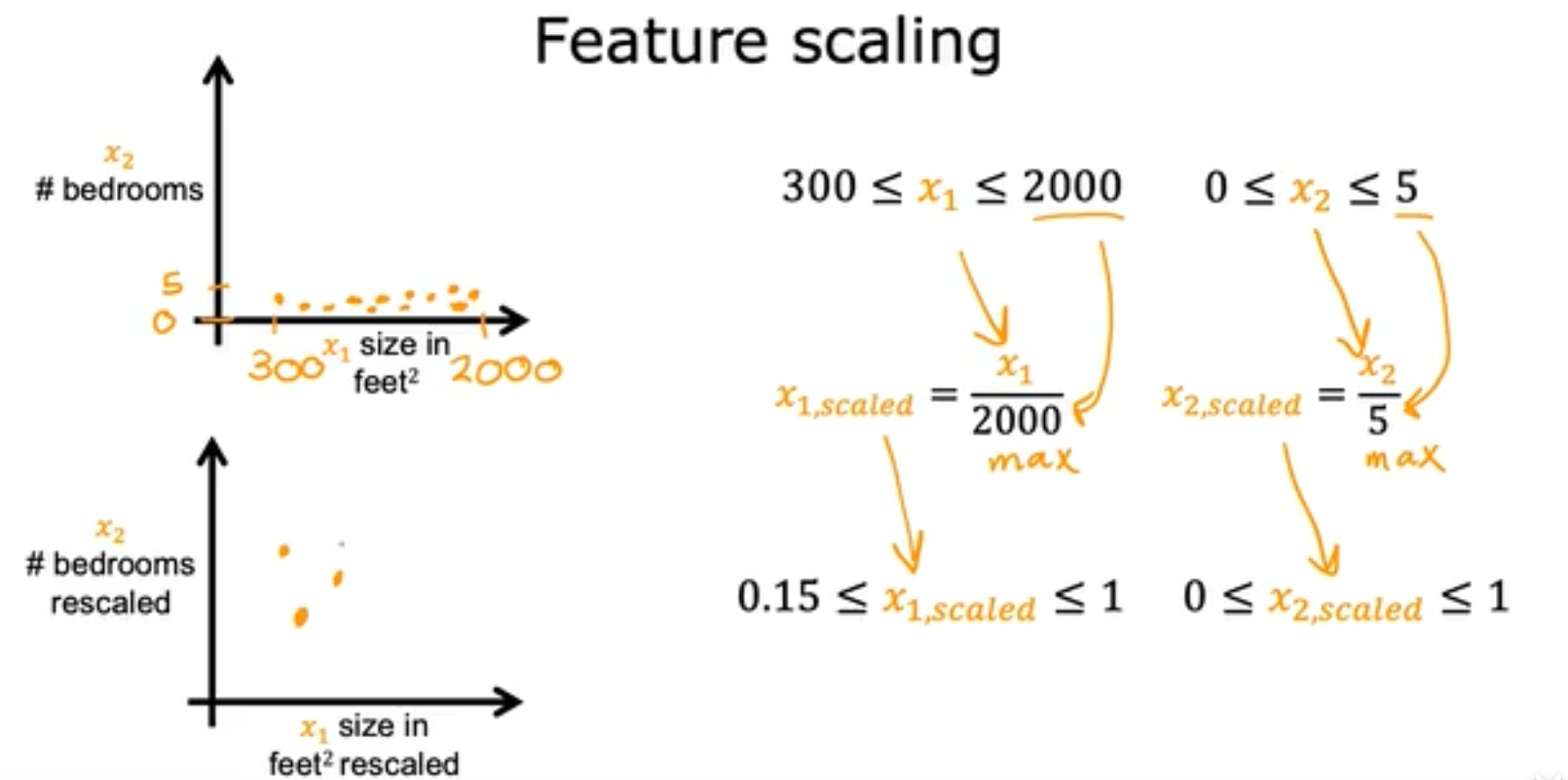
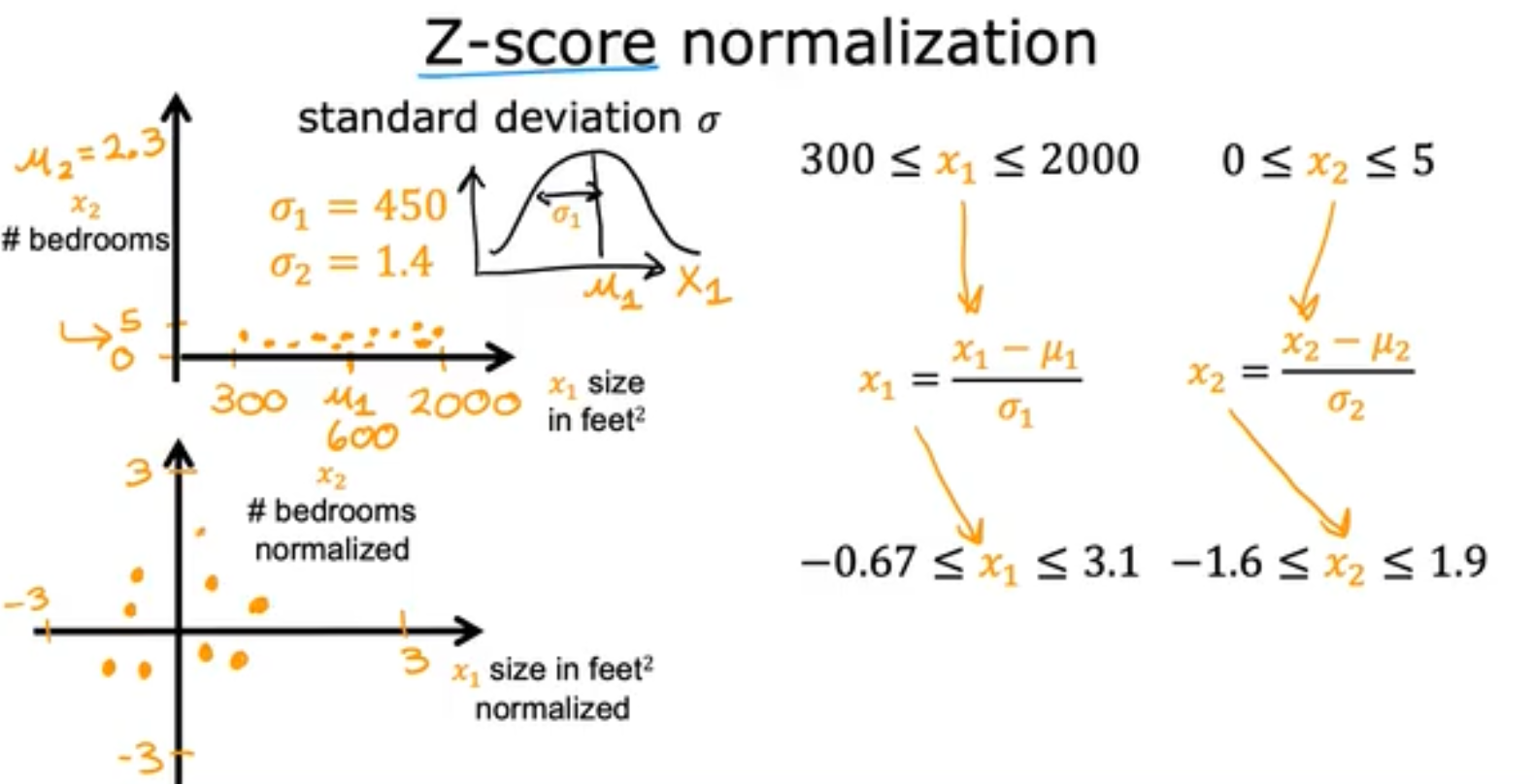
但是如果评估你是否应该进行feature scaling或者你的特征是否在一个合理的范围呢，即你需要将特征保持在一个数量级别，如[-3, 3]和[-2, 0.5]就是ok的，但是[-0.001, 0.001]以及[-100, 100]就是不ok的。

x.2 收敛与learning rate选取

我们进行feature scaling的目的是为了使得Gradient Descent算法收敛，那我们如何判断是否收敛呢？当你的J(w)不再下降时，就近乎于收敛了。

学习率的选择是非常重要的，如果对于J(w)和iterations（iterations应该是针对per batch的）的曲线而言，你的损失函数曲线是有上下振幅或者会变大，这往往意味着你的代码有Bug或者你的learning rate的选取太大。对于拥有正确learning rate的梯度下降算法而言，loss应该是逐步下降，

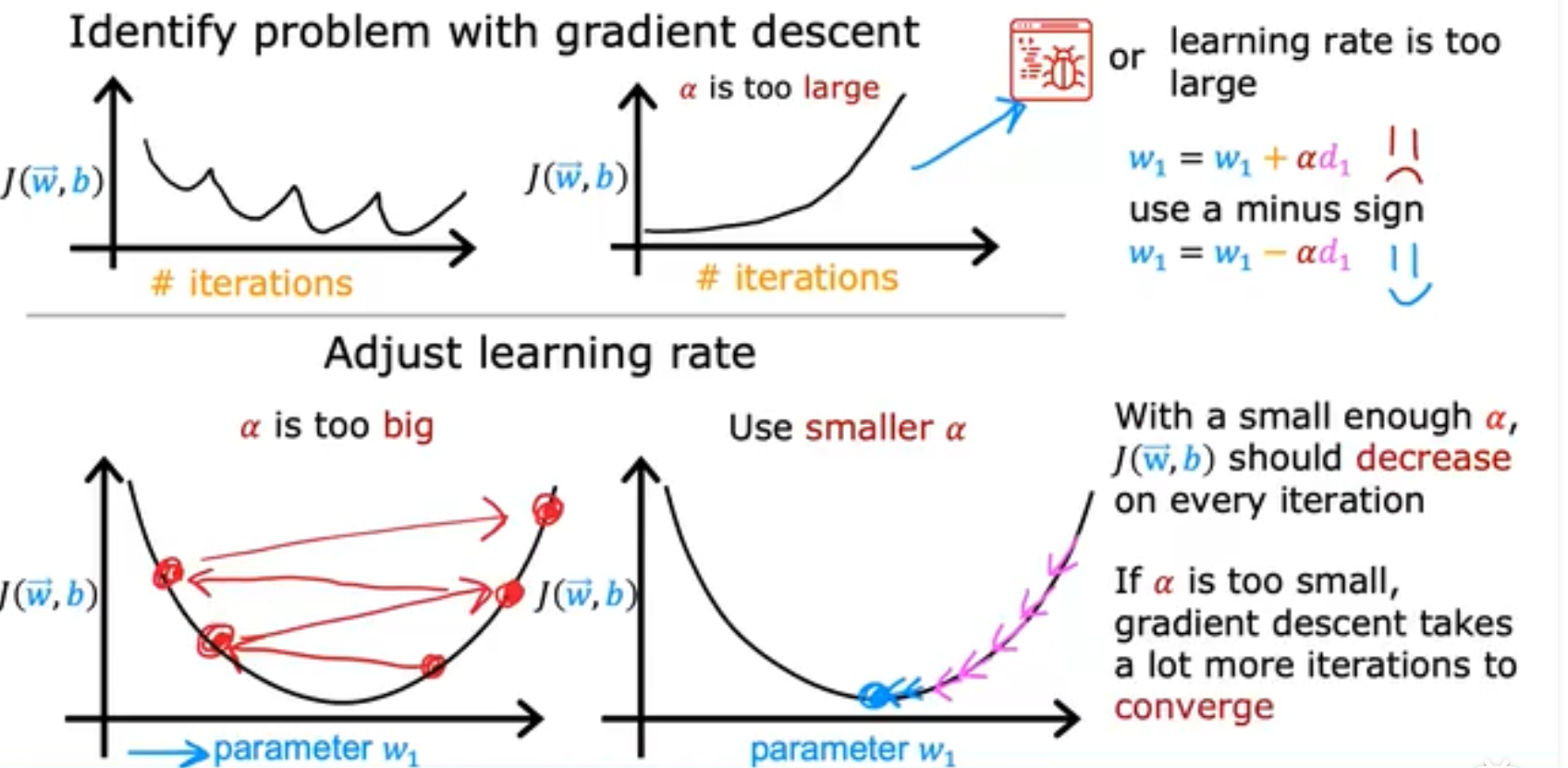
而learning rate是如何选取的呢？我们通常会从一个很小的learning rate开始进行筛选，例如0.001，如果J(w)-iterations的图像稳定下降，则再选取一个较大的learning rate直到J(w)-iterations图像开始出现上下抖动下降为止，当然，现在还有一些比较火的方法，例如余弦退活函数等等，

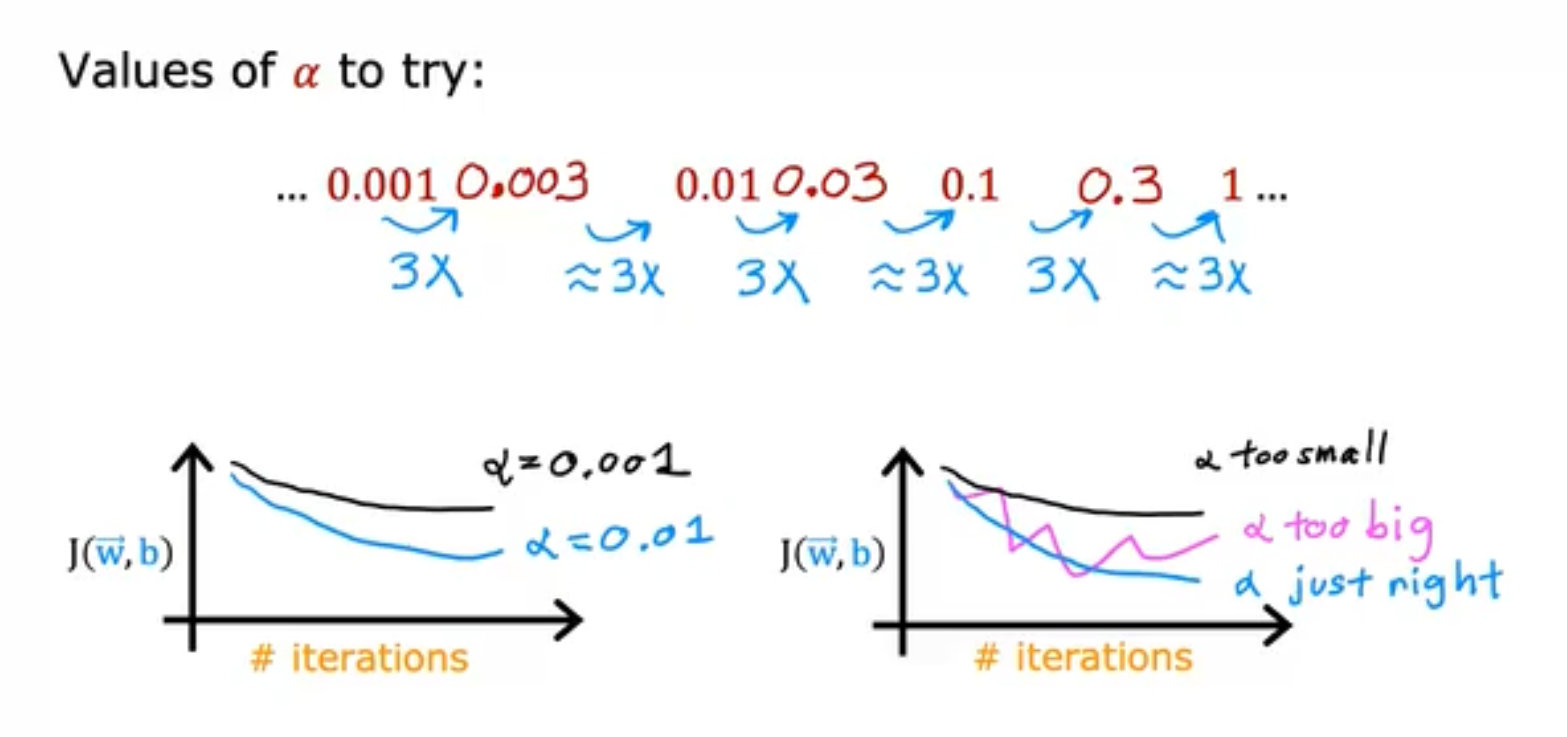
x.3 特征工程与特征选取

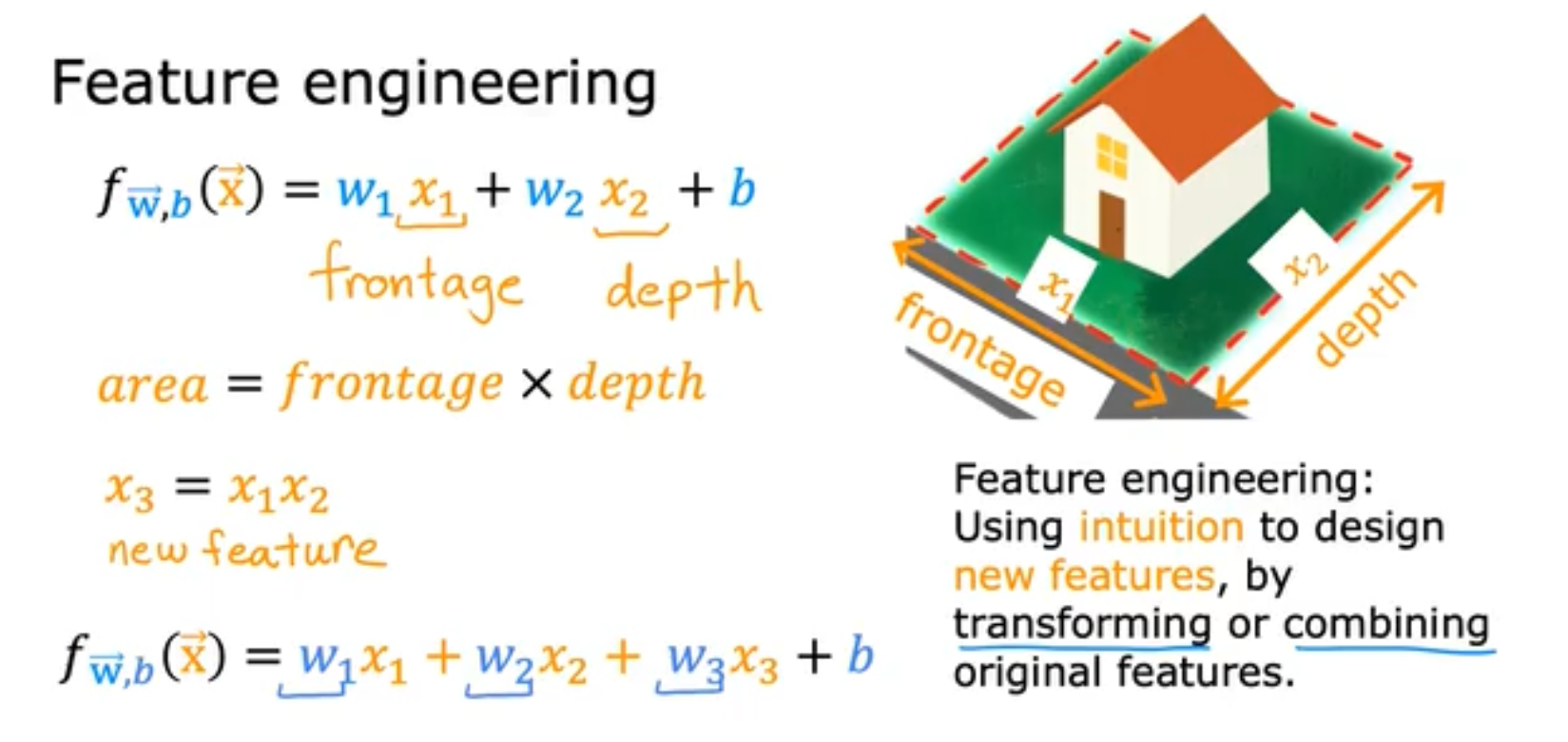
我们使用现有的特征来新建一个新的特征是特征工程里常用的手段，例如我们使用房子的长度乘以宽度得到房子的面积，用面积做特征，我们能够得到一个更好的模型。

当你的需要拟合的多项式是$$y=w_1\ast x_1^2+w_2\ast x_2^3$$时，你应该将$x_1^2和x_2^3$视为两个feature并进行特征缩放。