目录

法一、

法二、

---

题述：

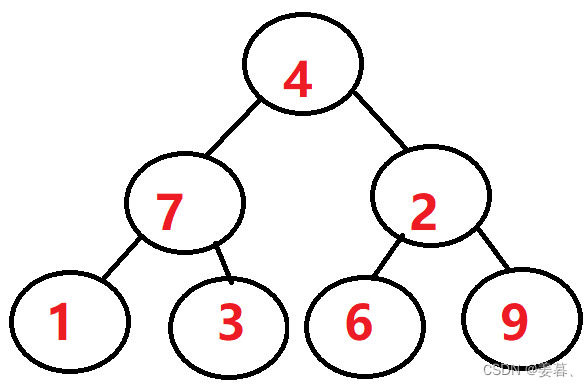
翻转一颗二叉树。

输入：

输出：

题中已给：

struct TreeNode
{
	int val;
	struct TreeNode* left;
	struct TreeNode* right;
};
TreeNode* invertTree(struct TreeNode* root)

法一、

思路：

类似于后序遍历：左右根。根节点无需交换，交换左右子树就好，不断递归，交换当前树的左右节点，再交换左右子树的左右节点......直到遇到空树，返回。

①、2和7交换

 ②、然后访问4的左子树(以7为根的树),然后交换1和3，再访问3的左子树(以1为根的树)，为NULL返回NULL，同理，3的右子树返回NULL，然后return root，即3，然后访问7的右子树1，同理3的访问，最后会返回root 1，至此7的左右子树访问完毕并完成交换，然后访问4的右子树2，同理，会会先交换6和9，然后不断递归，最后直到2的左右子树访问完毕会返回2，4的左右子树也访问完毕，返回根节点4，完成所有子树交换。

invertTree函数的功能：比如invertTree(root->left)就会完成以root->left为根节点的左右节点的交换

struct TreeNode* invertTree(struct TreeNode* root)
{
    //如果是空树，直接返回NULL，无需交换
	if (root == NULL)
	{
		return NULL;
	}
    //交换左右节点
	struct TreeNode* tmp = root->left;
	root->left = root->right;
	root->right = tmp;
    //递归左右子树
	invertTree(root->left);
	invertTree(root->right);

	return root;
}

法二、

思路： 

递归过程：

以4为根节点的左右子树，保存右子树7，7=invertTree(root->left),即下次调用传入根节点2,右子树=invertTree（2的左子树即以1为根的子树），1的左右子树均为NULL后,return 1,即2的右子树变为1，同理左子树会变为3。至此4的左子树访问完毕，同理4的右子树也是一样的访问过程，最后4的左右子树都访问完毕，会返回4,整棵树翻转完毕。

struct TreeNode* invertTree(struct TreeNode* root)
{
	if (root == NULL)
	{
		return NULL;
	}

	struct TreeNode* right = root->right;
	root->right = invertTree(root->left);
	root->left = invertTree(right);

	return root;
}