文章目录
- 2023.7.3——445. 两数相加 II(大数相加/高精度加法)
- 2023.7.4——2679. 矩阵中的和
- 2023.7.5——2600. K 件物品的最大和(贪心)
- 代码1——贪心模拟
- 代码2——Java一行
- 2023.7.6——2178. 拆分成最多数目的正偶数之和(贪心)⭐⭐⭐
- 思路
- 代码
- 2023.7.7——2532. 过桥的时间(复杂大模拟题)⭐⭐⭐⭐⭐
- 2023.7.8——167. 两数之和 II - 输入有序数组
- 解法1——双指针
- 解法2——二分查找
- 2023.7.9——15. 三数之和
- 排序 + 枚举第一个数 + 双指针处理后两个数 + 去重
- 代码优化
2023.7.3——445. 两数相加 II(大数相加/高精度加法)
445. 两数相加 II

这道题目考察的实际知识点是高精度加法。更多关于高精度计算的内容参见:【算法基础】1.4 高精度(模拟大数运算:整数加减乘除)
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
// 将两个链表的结果存成列表
List<Integer> ls1 = new ArrayList(), ls2 = new ArrayList(), ls = new ArrayList();
int carry = 0;
while (l1 != null) {
ls1.add(l1.val);
l1 = l1.next;
}
while (l2 != null) {
ls2.add(l2.val);
l2 = l2.next;
}
Collections.reverse(ls1);
Collections.reverse(ls2);
// 大数加法
for (int i1 = 0, i2 = 0, n1 = ls1.size(), n2 = ls2.size(); i1 < n1 || i2 < n2 || carry != 0; ++i1, ++i2) {
if (i1 < n1) carry += ls1.get(i1);
if (i2 < n2) carry += ls2.get(i2);
ls.add(carry % 10);
carry /= 10;
}
// 将列表转成链表结果
ListNode dummy = new ListNode(), t = dummy;
for (int i = ls.size() - 1; i >= 0; --i) {
ListNode cur = new ListNode(ls.get(i));
t.next = cur;
t = t.next;
}
return dummy.next;
}
}
2023.7.4——2679. 矩阵中的和
2679. 矩阵中的和
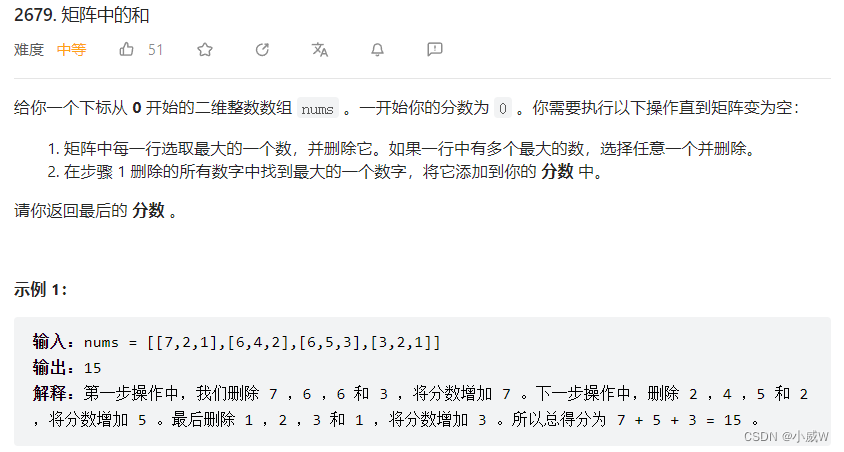
读懂题意,每次操作会删去每一行中的当前最大值,同时将这些行最大值中的最大值加入最后的分数。
为了快速模拟删去每行最大值的操作,我们可以先对各个行进行排序。
class Solution {
public int matrixSum(int[][] nums) {
int m = nums.length, n = nums[0].length;
for (int i = 0; i < m; ++i) Arrays.sort(nums[i]);
int ans = 0;
for (int j = 0; j < n; ++j) {
int mx = 0;
for (int i = 0; i < m; ++i) {
mx = Math.max(mx, nums[i][j]);
}
ans += mx;
}
return ans;
}
}
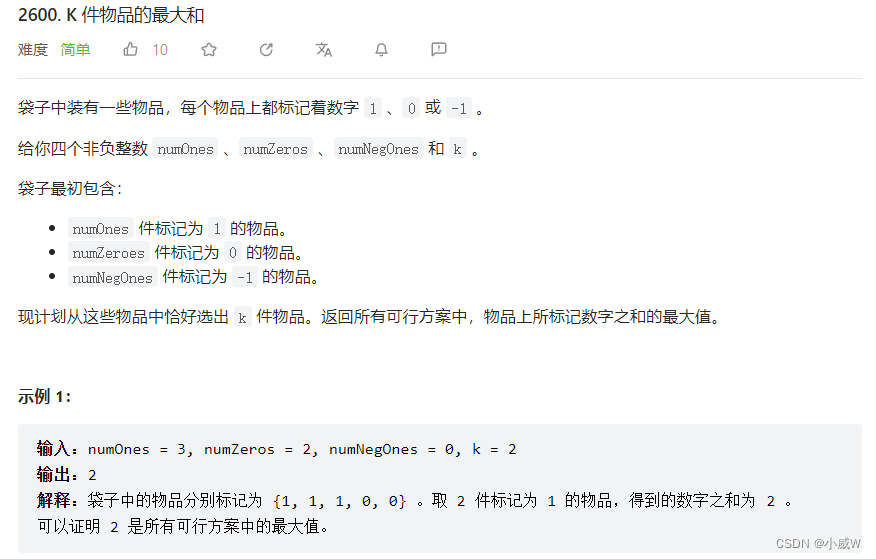
2023.7.5——2600. K 件物品的最大和(贪心)
2600. K 件物品的最大和
代码1——贪心模拟
要想数字之和最大,肯定先选 1,再选 0,最后选 -1。
class Solution {
public int kItemsWithMaximumSum(int numOnes, int numZeros, int numNegOnes, int k) {
int ans = 0;
ans += Math.min(numOnes, k);
k = k - numOnes - numZeros;
if (k > 0) ans -= Math.min(numNegOnes, k);
return ans;
}
}
代码2——Java一行
思想上没什么区别,代码比较优雅。
class Solution {
public int kItemsWithMaximumSum(int numOnes, int numZeros, int numNegOnes, int k) {
return Math.min(numOnes, k) - Math.max(k - numOnes - numZeros, 0);
}
}
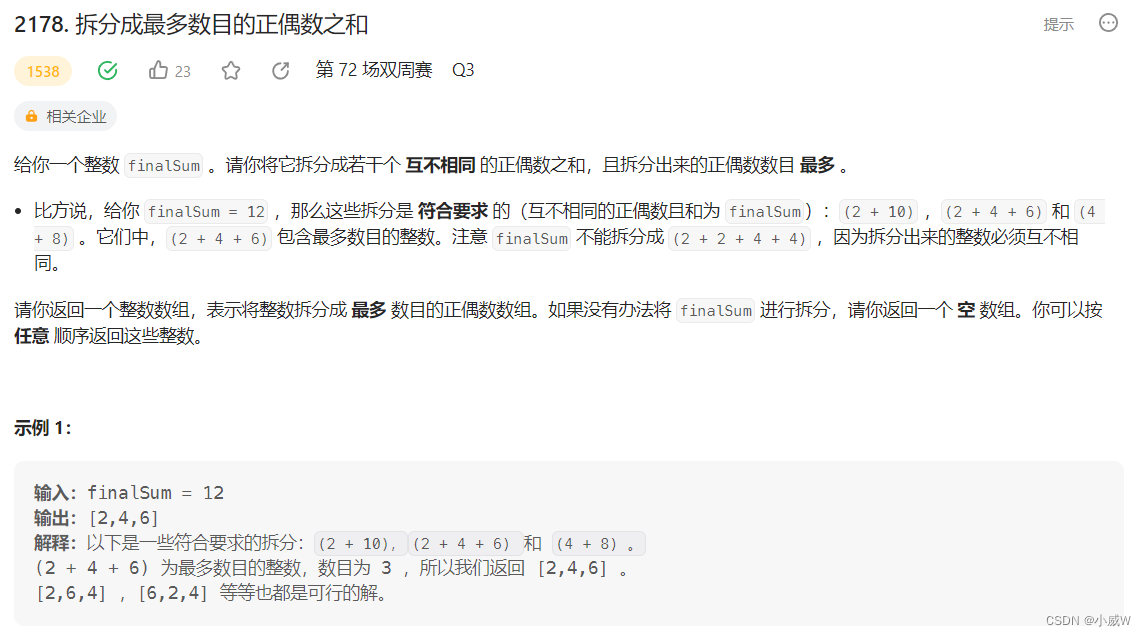
2023.7.6——2178. 拆分成最多数目的正偶数之和(贪心)⭐⭐⭐
2178. 拆分成最多数目的正偶数之和
思路

提示:
1 <= finalSum <= 10^10
代码
class Solution {
public List<Long> maximumEvenSplit(long finalSum) {
List<Long> ans = new ArrayList();
if (finalSum % 2 == 1) return ans;
long sum = 0, num = 2;
for (long i = 2; i <= finalSum; i += 2) {
ans.add(i);
finalSum -= i;
}
ans.set(ans.size() - 1, ans.get(ans.size() - 1) + finalSum);
return ans;
}
}
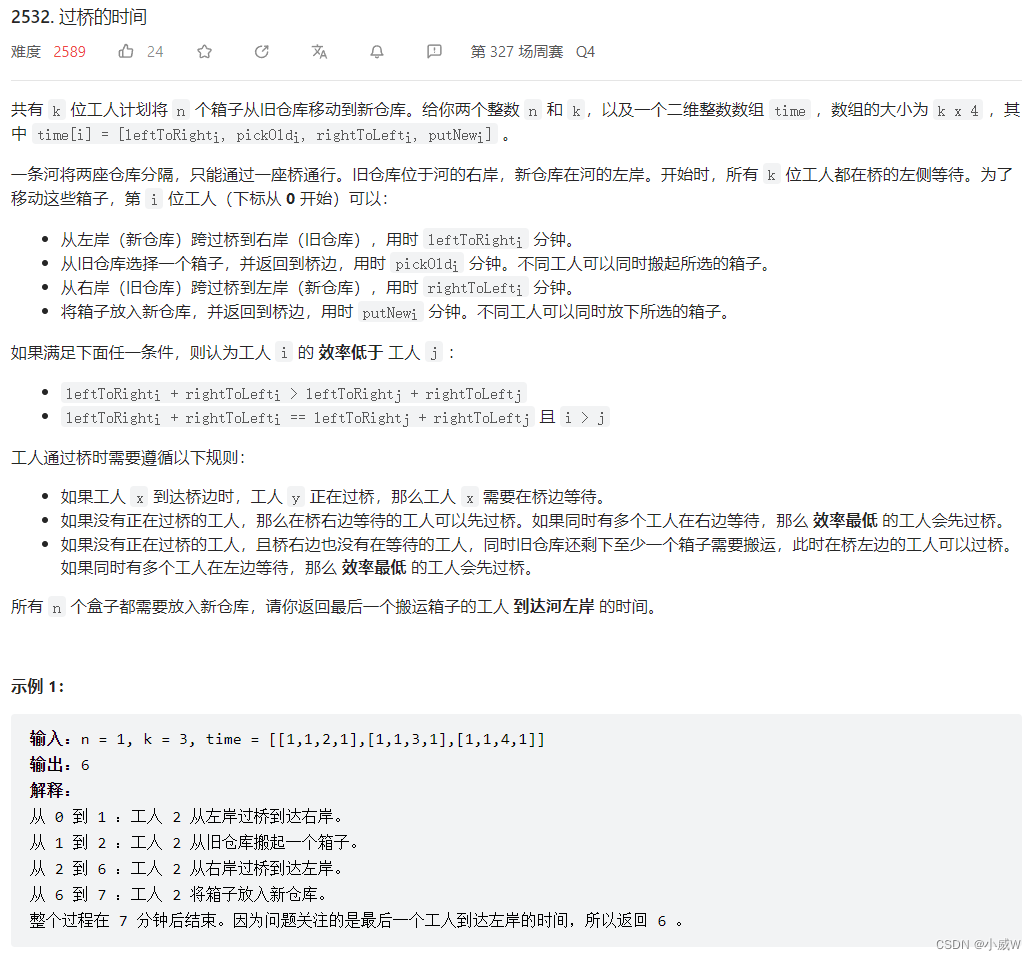
2023.7.7——2532. 过桥的时间(复杂大模拟题)⭐⭐⭐⭐⭐
2532. 过桥的时间
提示:
1 <= n, k <= 10^4
time.length == k
time[i].length == 4
1 <= leftToRighti, pickOldi, rightToLefti, putNewi <= 1000
做这种复杂模拟题,一定要仔细读题!

class Solution {
public int findCrossingTime(int n, int k, int[][] time) {
Arrays.sort(time, (a, b) -> {
return a[0] + a[2] - b[0] - b[2];
}); // 排序之后下标越大的工人效率越低
PriorityQueue<int[]> workL = new PriorityQueue<int[]>((a, b) -> a[1] - b[1]); // 按完成时间升序排序
PriorityQueue<int[]> workR = new PriorityQueue<int[]>(workL.comparator());
PriorityQueue<int[]> waitL = new PriorityQueue<int[]>((a, b) -> b[0] - a[0]); // 效率低的排前面
PriorityQueue<int[]> waitR = new PriorityQueue<int[]>(waitL.comparator());
// 都先加入在左边的等待队列
for (int i = k - 1; i >= 0; --i) waitL.offer(new int[]{i, 0});
int cur = 0;
while (n > 0) {
// 左边完成放箱
while (!workL.isEmpty() && workL.peek()[1] <= cur) waitL.offer(workL.poll());
// 右边完成搬箱
while (!workR.isEmpty() && workR.peek()[1] <= cur) waitR.offer(workR.poll());
// 先看右边有没有人等着
if (!waitR.isEmpty()) {
int[] p = waitR.poll();
cur += time[p[0]][2]; // 从右到左的时间
p[1] = cur + time[p[0]][3]; // 加上在左边工作的时间放入左边工作队列
workL.offer(p);
} else if (!waitL.isEmpty()) { // 再看左边有没有人等着过桥
int[] p = waitL.poll();
cur += time[p[0]][0];
p[1] = cur + time[p[0]][1];
workR.offer(p);
--n; // 只要左边的人过去了,就把 n - 1,这样就可以保证所有箱子都有人搬运之后左边就不会有人再过桥了
} else if (workL.isEmpty()) cur = workR.peek()[1]; // cur过小,找下一个最近的完成时间
else if (workR.isEmpty()) cur = workL.peek()[1];
else cur = Math.min(workL.peek()[1], workR.peek()[1]);
}
// 循环退出时是所有需要搬运箱子的人都过桥到右边去了,因此需要再处理右边的工作队列
// 答案就是这些人中最后完成过桥的人
// 注意答案要求是最后一个工人达到河左岸的时间,而不是放下箱子的时间
while (!workR.isEmpty()) {
int[] p = workR.poll();
cur = Math.max(p[1], cur) + time[p[0]][2];
}
return cur;
}
}
注意点1:什么时候 --n ?
当有足够多的人去到右边之后就 --n。
注意点2:答案怎么返回?
答案就是最后一个从右边回来的人过完桥之后的时间。
2023.7.8——167. 两数之和 II - 输入有序数组
167. 两数之和 II - 输入有序数组
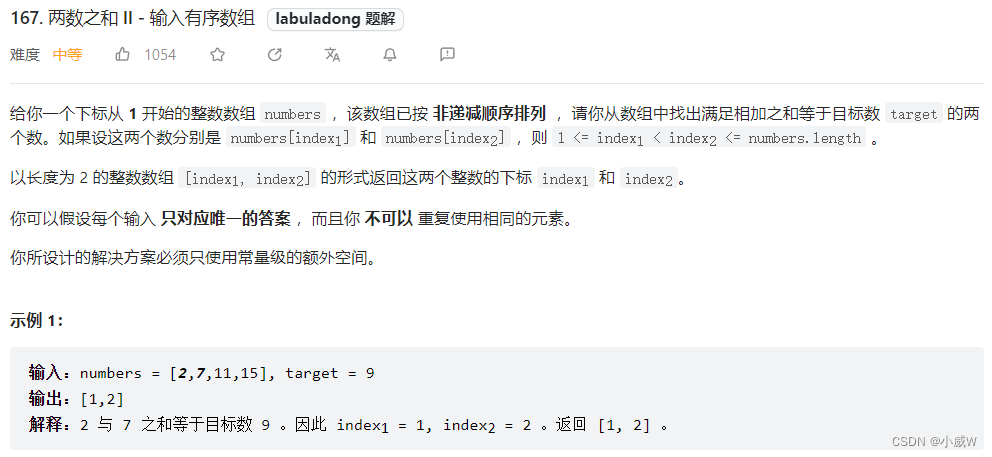
提示:
2 <= numbers.length <= 3 * 10^4
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案
解法1——双指针
class Solution {
public int[] twoSum(int[] numbers, int target) {
int l = 0, r = numbers.length - 1;
while (l < r) {
int x = numbers[l] + numbers[r];
if (x == target) return new int[]{l + 1, r + 1};
else if (x < target) l++;
else r--;
}
return new int[]{-1, -1};
}
}
时间复杂度是: O ( n ) O(n) O(n)
解法2——二分查找
枚举每个位置,然后二分查找是否存在和它配对的即可。
时间复杂度是: O ( n ∗ log n ) O(n*\log{}{n}) O(n∗logn)
2023.7.9——15. 三数之和
15. 三数之和
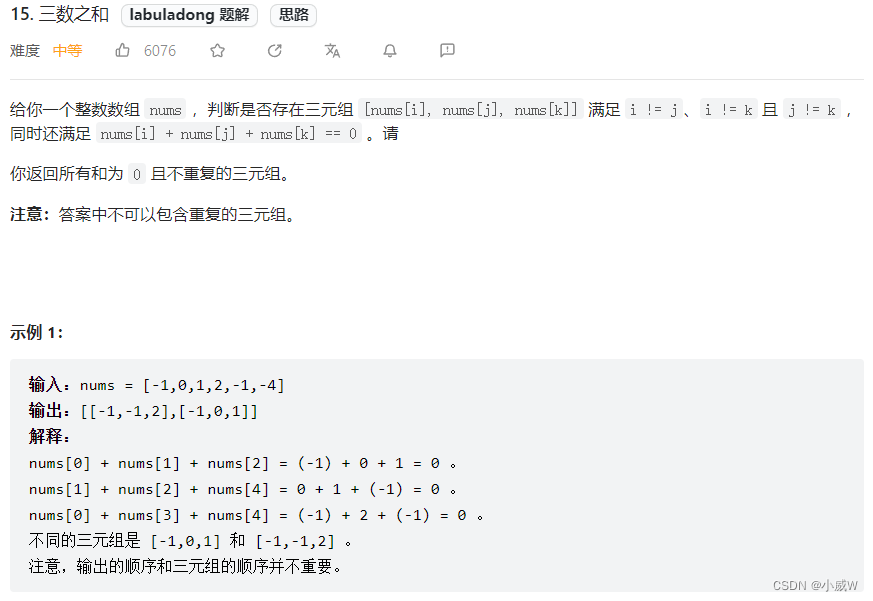
提示:
3 <= nums.length <= 3000
-10^5 <= nums[i] <= 10^5
排序 + 枚举第一个数 + 双指针处理后两个数 + 去重
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> ans = new ArrayList();
int n = nums.length;
for (int i = 0; i < n - 2; ++i) {
if (i > 0 && nums[i] == nums[i - 1]) continue; // 去重
int target = -nums[i];
for (int l = i + 1, r = n - 1; l < r; ) {
int sum = nums[l] + nums[r];
if (sum == target) {
ans.add(List.of(nums[i], nums[l], nums[r])); // 加入答案
do l++; while (l <= r && nums[l] == nums[l - 1]);
do r--; while (r >= l && nums[r] == nums[r + 1]);
} else if (sum < target) ++l;
else --r;
}
}
return ans;
}
}
这里的去重是通过排序后相同元素必定相邻,比较相邻元素是否相等来实现去重的。
代码优化
class Solution {
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> ans = new ArrayList();
int n = nums.length;
for (int i = 0; i < n - 2; ++i) {
if (i > 0 && nums[i] == nums[i - 1]) continue; // 去重
int target = -nums[i];
if (nums[i + 1] + nums[i + 2] > target) break; // 优化1
if (nums[n - 1] + nums[n - 2] < target) continue; // 优化2
for (int l = i + 1, r = n - 1; l < r; ) {
int sum = nums[l] + nums[r];
if (sum == target) {
ans.add(List.of(nums[i], nums[l], nums[r])); // 加入答案
do l++; while (l <= r && nums[l] == nums[l - 1]);
do r--; while (r >= l && nums[r] == nums[r + 1]);
} else if (sum < target) ++l;
else --r;
}
}
return ans;
}
}
加了两个小优化,速度从 37ms 加速到了 27ms。
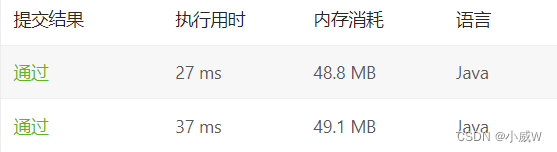
优化1指:当前最小的两个数之和都大于 target 了,之后的 target 会越来越小,所以直接 break。
优化2指:当前最大的两个数之和小于 target,这次循环是不行了,看看之后的 target 变小之后有没有合理的答案。