前言
- 本文着重介绍数据分析实战的基础知识和技巧,探索从数据探索到建模再到模型解释的完整过程
- 内容包含数据探索、模型建立、调参技巧、SHAP模型解释
- 数据来源于kaggle平台,crab age prediction数据集,数据详情
数据说明
数据背景
螃蟹味道鲜美,世界上许多国家每年都会进口大量螃蟹供消费。螃蟹养殖的主要优点是劳动力成本很低,生产成本相对较低,而且生长速度很快。商业螃蟹养殖业正在发展沿海地区人民的生活方式。通过适当的照顾和管理,我们从螃蟹养殖业中可以获得比养虾业更多的收入。您可以在两个系统中饲养青蟹。发展农业和育肥系统。
数据价值
对于商业蟹农来说,了解螃蟹的正确年龄有助于他们决定是否以及何时收获螃蟹。超过一定年龄后,螃蟹的物理特性的增长可以忽略不计,因此,把握收获时间以降低成本并增加利润非常重要。该数据集的目标是:
- 探索性数据分析 - 了解不同的身体特征如何随年龄变化。
- 特征工程 - 使用给定数据点的组合定义新特征,以帮助提高模型准确性。
- 回归模型 - 构建回归模型来预测螃蟹的年龄。
数据字段
Sex:螃蟹的性别——雄性(M)、雌性(F)和不确定(I)。Length:螃蟹的长度(以英尺为单位;1 英尺 = 30.48 厘米)Diameter:螃蟹的直径(以英尺为单位;1 英尺 = 30.48 厘米)Height:螃蟹的高度(以英尺为单位;1 英尺 = 30.48 厘米)Weight:螃蟹的重量(以盎司为单位;1 磅 = 16 盎司)Shucked Weight:不含壳的重量(以盎司为单位;1 磅 = 16 盎司)Viscera Weight:身体深处腹部器官的重量(以盎司为单位;1 磅 = 16 盎司)Shell Weight:外壳重量(盎司;1 磅 = 16 盎司)Age:螃蟹的年龄(月)
依赖包
pandas:读取数据,基础包ydata-profiling:快速数据探索包,Github项目地址,官方文档sklearn:经典的机器学习模型包,这里不过多介绍shap:SHAP(SHapley Additive exPlanations)是一种博弈论方法,用于解释任何机器学习模型的输出。它将最优信用分配与局部解释联系起来,使用博弈论中的经典Shapley值及其相关扩展(有关详细信息和引文,请参阅论文)。- 下面的分析都基于以上包的支持,请提前使用
pip install进行安装,如果是在Jupyter Notebook中使用,请使用```!pip install``。
导入必要包
import numpy as np
import pandas as pd
from plotnine import*
import seaborn as sns
from scipy import stats
import matplotlib as mpl
import matplotlib.pyplot as plt
#中文显示问题
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False
# notebook嵌入图片
%matplotlib inline
# 提高分辨率
%config InlineBackend.figure_format='retina'
from ydata_profiling import ProfileReport
import shap
# 忽略警告
import warnings
warnings.filterwarnings('ignore')
导入数据
df = pd.read_csv('/kaggle/input/crab-age-prediction/CrabAgePrediction.csv')
df.head()
输出:
Sex Length Diameter Height Weight Shucked Weight Viscera Weight Shell Weight Age
0 F 1.4375 1.1750 0.4125 24.635715 12.332033 5.584852 6.747181 9
1 M 0.8875 0.6500 0.2125 5.400580 2.296310 1.374951 1.559222 6
2 I 1.0375 0.7750 0.2500 7.952035 3.231843 1.601747 2.764076 6
3 F 1.1750 0.8875 0.2500 13.480187 4.748541 2.282135 5.244657 10
4 I 0.8875 0.6625 0.2125 6.903103 3.458639 1.488349 1.700970 6
数据分析
profile = ProfileReport(df, title="Crab data report")
profile.to_notebook_iframe()
- 由于CSDN无法内嵌html文件,这里只能将完整的数据报告拆分,分开讲解。
概述

- 从上图中可获知以下信息:
- 数据一共包含9个特征
- 数据一共有3893个样本
- 数据样本没有任何缺失与重复
- 分类变量有1个,其他8个为数值变量
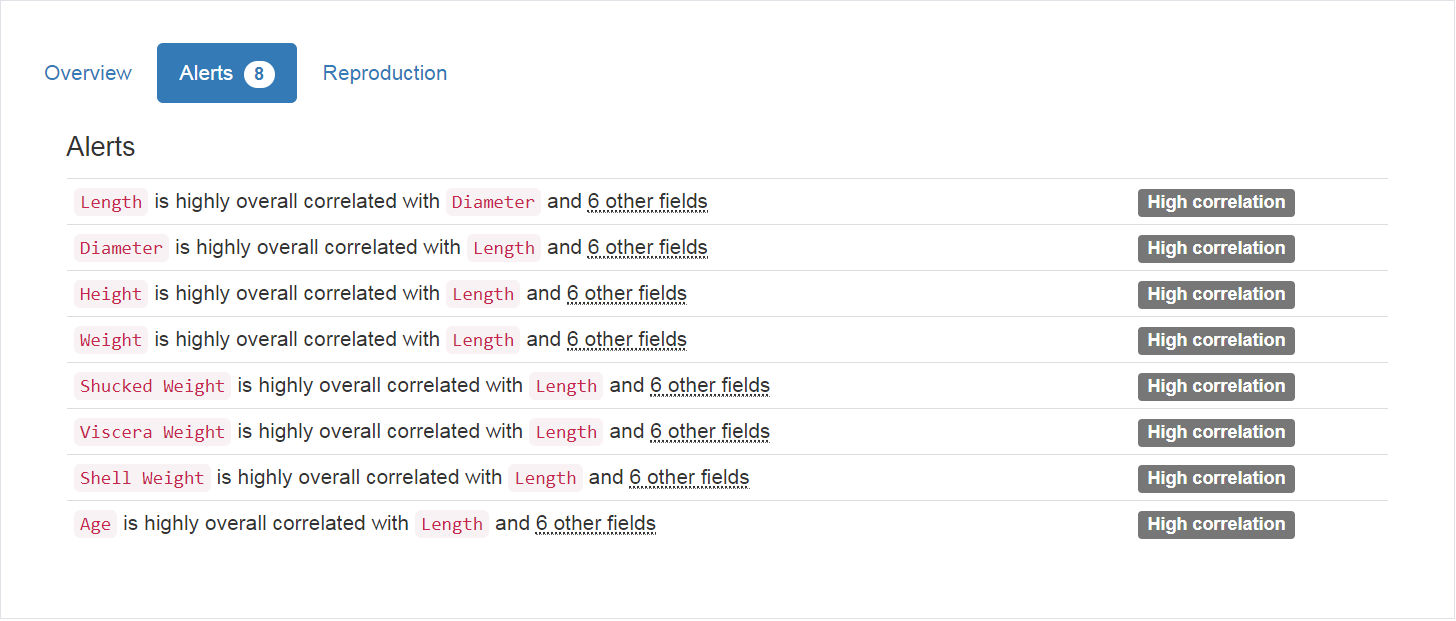
- 从上图中可获知以下信息:
- 特征
Length与Diameter有较强的相关性 - 特征
Length与Height有较强的相关性 - 特征
Length与Weight有较强的相关性 - 特征
Length与Shucked Weight有较强的相关性 - 特征
Length与Viscera Weight有较强的相关性 - 特征
Length与Shell Weight有较强的相关性 - 特征
Length与Age有较强的相关性
- 特征
变量

- 从上图中可获知以下信息:
- 特征
Sex为类别变量,一共有3类 - 其中类别
M的样本有1435条、类别I的样本有1233条、类别F的样本有1225条

- 特征
- 从上图中可获知以下信息:
- 特征
Length为数值变量,一共出现了134个值,差异比例为3.4% - 根据直方图可以看到数据分布呈一定右偏
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Diameter为数值变量,一共出现了111个值,差异比例为2.9% - 根据直方图可以看到数据分布呈一定右偏
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Height为数值变量,一共出现了51个值,差异比例为1.3% - 根据直方图可以看到数据分布呈正态分布,但最大值为2.825,有点异常,可能要考虑剔除。
- 0值有2个,占总体样本的0.1%,根据经验长度不可能为0,所以这2个样本可能为异常样本,需要剔除。
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Weight为数值变量,一共出现了2343个值,差异比例为60.2% - 根据直方图可以看到数据分布呈一定左偏,60以后的值需要考虑是否为潜在异常值,并对其进行相应处理
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Shucked Weight为数值变量,一共出现了1482个值,差异比例为38.1% - 根据直方图可以看到数据分布呈一定左偏,30以后的值需要考虑是否为潜在异常值,并对其进行相应处理
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Viscera Weight为数值变量,一共出现了867个值,差异比例为22.3% - 根据直方图可以看到数据分布呈一定左偏,15以后的值需要考虑是否为潜在异常值,并对其进行相应处理
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Shell Weight为数值变量,一共出现了907个值,差异比例为23.3% - 根据直方图可以看到数据分布呈一定左偏,20以后的值需要考虑是否为潜在异常值,并对其进行相应处理
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等

- 特征
- 从上图中可获知以下信息:
- 特征
Age为数值变量,一共出现了28个值,差异比例为0.7% - 根据直方图可以看到数据分布基本呈正态分布,25以后的值需要考虑是否为潜在异常值,并对其进行相应处理
- 获知该特征的各类统计特征,如最大最小值、平均值、四分位数等等
- 特征
交互作用图
- 这里可以选择不同的两个变量,因为篇幅有限,这里只展示纵轴为
Weight,横轴为Age的交互图。

相关性图

- 上面图中展现的高相关性信息在概述阶段已经说明了,这里就不再赘述了。
数据处理
- 根据上述数据分析,对数据进行相应处理
- 将特征
Height中为0的样本进行剔除 - 因为
Sex无大小关系,所以对其进行独热编码,使用df = pd.get_dummies(df,columns=["Sex"]) - 使用
sklearn中的隔离森林算法剔除潜在异常值,异常值占比为0.05(经验数值) - 将数据进行标准化(
zscore)变换,由于数据量较小,训练集为0.9,测试集为0.1,使用10折交叉检验平均MSE作为评估标准 - 以Age为因变量,其余特征为自变量,构建回归模型
建立模型与调参
- 使用sklearn构建多种回归模型,如
gbr、catboost、lightgbm等
| ID | Model | MAE | MSE | RMSE | R2 | RMSLE | MAPE | TT (Sec) |
|---|---|---|---|---|---|---|---|---|
| gbr | Gradient Boosting Regressor | 1.5019 | 4.4889 | 2.1169 | 0.5530 | 0.1727 | 0.1501 | 0.3410 |
| catboost | CatBoost Regressor | 1.5082 | 4.5334 | 2.1277 | 0.5485 | 0.1729 | 0.1505 | 2.6590 |
| lightgbm | Light Gradient Boosting Machine | 1.5240 | 4.6280 | 2.1504 | 0.5389 | 0.1751 | 0.1516 | 0.4320 |
| rf | Random Forest Regressor | 1.5338 | 4.6551 | 2.1561 | 0.5363 | 0.1762 | 0.1535 | 0.8190 |
| et | Extra Trees Regressor | 1.5494 | 4.7462 | 2.1772 | 0.5267 | 0.1780 | 0.1552 | 0.4890 |
| ridge | Ridge Regression | 1.5771 | 4.8477 | 2.1979 | 0.5166 | 0.1824 | 0.1596 | 0.0430 |
| lr | Linear Regression | 1.5772 | 4.8479 | 2.1980 | 0.5165 | 0.1822 | 0.1596 | 0.4730 |
| lar | Least Angle Regression | 1.5772 | 4.8479 | 2.1980 | 0.5165 | 0.1822 | 0.1596 | 0.0470 |
| br | Bayesian Ridge | 1.5771 | 4.8482 | 2.1980 | 0.5166 | 0.1824 | 0.1596 | 0.0440 |
| huber | Huber Regressor | 1.5435 | 4.9130 | 2.2136 | 0.5105 | 0.1814 | 0.1503 | 0.0620 |
| xgboost | Extreme Gradient Boosting | 1.5884 | 5.0390 | 2.2429 | 0.4972 | 0.1822 | 0.1581 | 0.2910 |
| knn | K Neighbors Regressor | 1.6147 | 5.1607 | 2.2705 | 0.4856 | 0.1853 | 0.1599 | 0.0500 |
| omp | Orthogonal Matching Pursuit | 1.8157 | 6.1171 | 2.4715 | 0.3917 | 0.2084 | 0.1867 | 0.0400 |
| en | Elastic Net | 1.8855 | 6.6865 | 2.5833 | 0.3367 | 0.2212 | 0.2007 | 0.0440 |
| lasso | Lasso Regression | 1.9536 | 7.1238 | 2.6663 | 0.2937 | 0.2360 | 0.2154 | 0.0440 |
| llar | Lasso Least Angle Regression | 1.9536 | 7.1238 | 2.6663 | 0.2937 | 0.2360 | 0.2154 | 0.0420 |
| ada | AdaBoost Regressor | 2.2463 | 7.2386 | 2.6873 | 0.2767 | 0.2325 | 0.2479 | 0.1820 |
| dt | Decision Tree Regressor | 2.0626 | 8.9308 | 2.9865 | 0.1079 | 0.2389 | 0.2035 | 0.0530 |
| par | Passive Aggressive Regressor | 2.2911 | 9.0001 | 2.9784 | 0.0897 | 0.2636 | 0.2401 | 0.0480 |
| dummy | Dummy Regressor | 2.3369 | 10.0990 | 3.1743 | -0.0006 | 0.2871 | 0.2672 | 0.0990 |
- 可以发现,
gbr模型的MSE最低,效果最好。使用随机搜索,调整参数,迭代20次,最佳模型10折交叉检验结果。
| Fold | MAE | MSE | RMSE | R2 | RMSLE | MAPE |
|---|---|---|---|---|---|---|
| 0 | 1.5267 | 4.7045 | 2.1690 | 0.5536 | 0.1719 | 0.1519 |
| 1 | 1.4646 | 4.3281 | 2.0804 | 0.5695 | 0.1674 | 0.1447 |
| 2 | 1.5053 | 4.3746 | 2.0915 | 0.5534 | 0.1757 | 0.1562 |
| 3 | 1.4995 | 4.5526 | 2.1337 | 0.5466 | 0.1731 | 0.1512 |
| 4 | 1.5798 | 4.6405 | 2.1542 | 0.5627 | 0.1842 | 0.1652 |
| 5 | 1.3879 | 3.7092 | 1.9259 | 0.6079 | 0.1654 | 0.1462 |
| 6 | 1.5613 | 4.8066 | 2.1924 | 0.5326 | 0.1744 | 0.1508 |
| 7 | 1.4739 | 4.4213 | 2.1027 | 0.5899 | 0.1683 | 0.1440 |
| 8 | 1.4873 | 4.5554 | 2.1343 | 0.6052 | 0.1716 | 0.1502 |
| 9 | 1.4654 | 4.0750 | 2.0187 | 0.4792 | 0.1658 | 0.1471 |
| Mean | 1.4952 | 4.4168 | 2.1003 | 0.5601 | 0.1718 | 0.1508 |
| Std | 0.0515 | 0.3082 | 0.0748 | 0.0359 | 0.0053 | 0.0060 |
- 最优参数如下:
| Param | nums |
|---|---|
| alpha | 0.9 |
| ccp_alpha | 0.0 |
| criterion | friedman_mse |
| init | None |
| learning_rate | 0.1 |
| loss | squared_error |
| max_depth | 3 |
| max_features | None |
| max_leaf_nodes | None |
| min_impurity_decrease | 0.0 |
| min_samples_leaf | 1 |
| min_samples_split | 2 |
| min_weight_fraction_leaf | 0.0 |
| n_estimators | 100 |
| n_iter_no_change | None |
| random_state | 2023 |
| subsample | 1.0 |
| tol | 0.0001 |
| validation_fraction | 0.1 |
| verbose | 0 |
| warm_start | False |
模型分析
- 对模型进行分析,可视化一些指标
模型残差图

- 模型在训练集与测试集上 R 2 R^2 R2相差不大,说明未发生过拟合现象
- 残差均匀分布在0线两侧,且呈现随机性
- 模型在训练集与测试集上残差分布基本一致
模型学习曲线
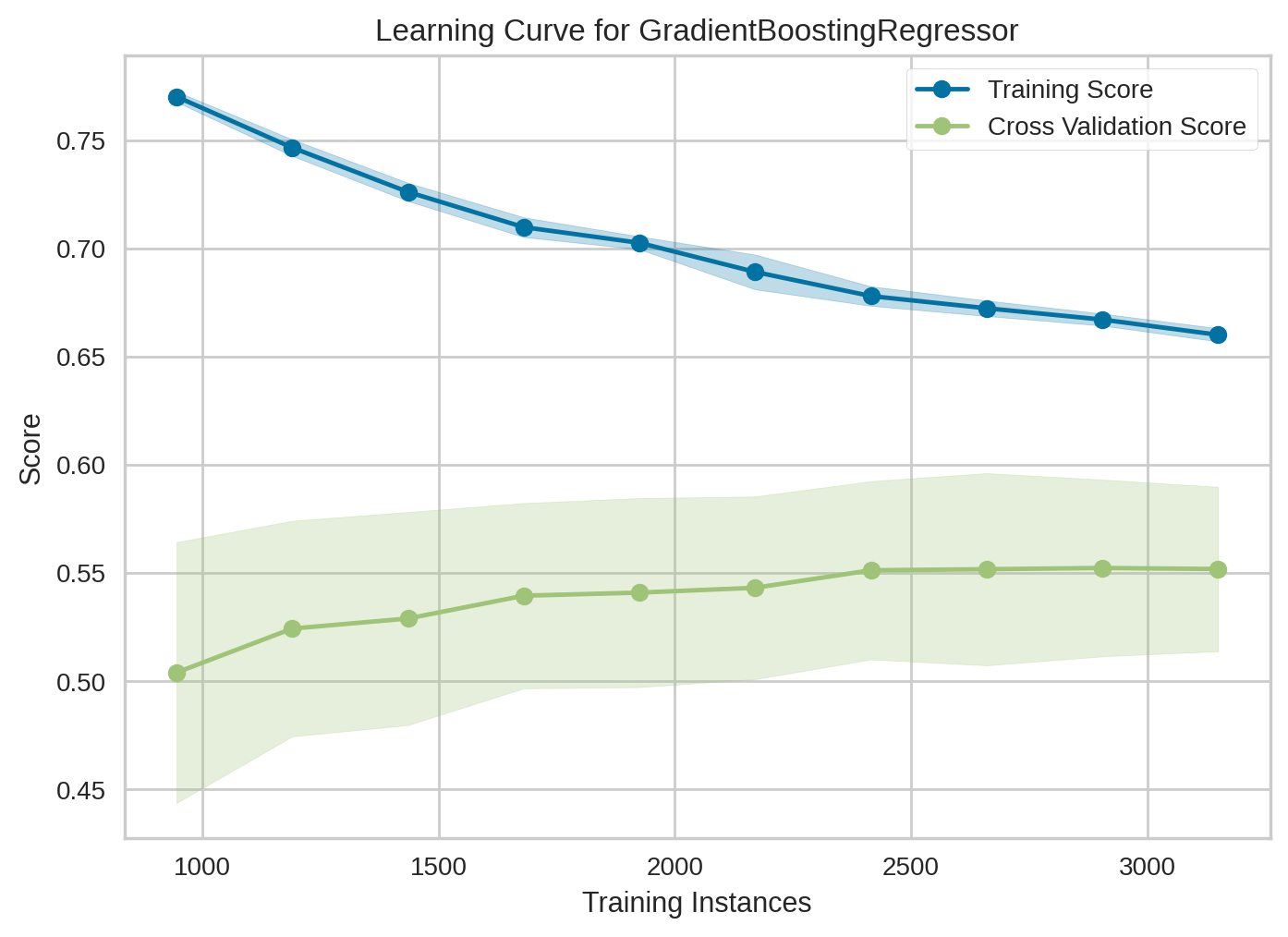
- 通过学习曲线我们可以判断模型是否产生了过拟合现象,可以看到上图中训练集和验证集都在往中间数值收敛,说明模型未参生过拟合现象。
模型解释
- 这一模块要用到SHAP包了,使用Shapley值评估特征对模型的影响。
力图
- 我们可以取出一个样本,然后可视化其预测过程,代码如下
# 取训练数据
X = s.get_config('X_train')
explainer = shap.TreeExplainer(model)
shap_values = explainer.shap_values(X)
shap.force_plot(explainer.expected_value, shap_values[0,:], X.iloc[0,:])

- 红色的代表特征贡献的正方向力(将预测推高),蓝色的表示特征贡献的负方向的力(将预测推低)
部分依赖图
- 为了解单个特征如何影响模型的输出以及特征间的交互作用,我们可以绘制部分依赖图
- 部分预测图遵照下列规则
- 每个点都是数据集中的一个样本
x轴是特征的值(来自X矩阵,存储在shap_values.data中)y轴是该特征的SHAP值(存储在shap_values.values中)。它表示了该特征的值会在多大程度上改变该样本预测的模型输出。对于这个模型,单位是Age的对数赔率。- 散点图的颜色由另一个特征决定,如果不传入固定特征,则函数会挑选与分析特征交互最强的特征列(比如在下面与
Length交互性最强的是Sex_F)
- 我们绘制出除
Sex独热编码后的其余列,并让函数自动选择与其交互性较强的特征
for name in X.columns:
if 'Sex' not in name:
shap.dependence_plot(name, shap_values, X)

- 由上图可知:
- 与
Length交互性最强的是Sex_F - 长度在1.25以上的雌性螃蟹年龄高于雄性和未知性别螃蟹
- 长度在1.00以下时,随着长度增加年龄也随着增加,但超过1.00以上时,长度增加年龄不一定增加

- 与
- 由上图可知:
- 与
Diameter交互性最强的是Sex_M - 螃蟹直径小于0.6时,直径越长,年龄越小。当直径在0.6~0.8时,直径越长,年龄越大,当直径超过0.8时,直径对年龄影响较小
- 直径在0.7以下时,雄性螃蟹年龄基本大于雌性和未知性别
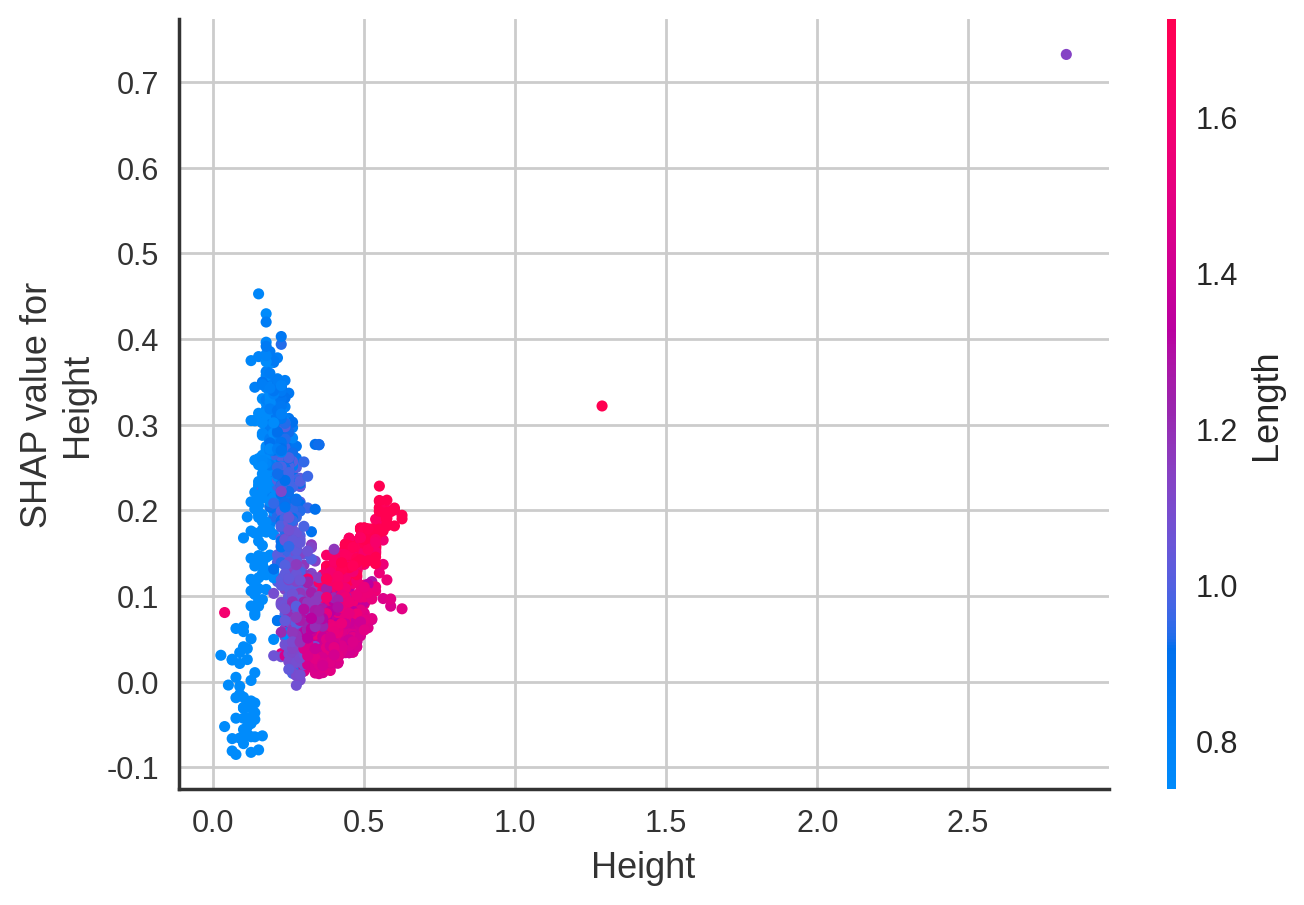
- 与
- 由上图可知:
- 与
Height交互性最强的是Length - 螃蟹高度大于0.3时,长度大的螃蟹年龄更大

- 与
- 由上图可知:
- 与
Weight交互性最强的是Sex_M - 在重量相同时,雄性螃蟹年龄比雌性和未知性别年龄大
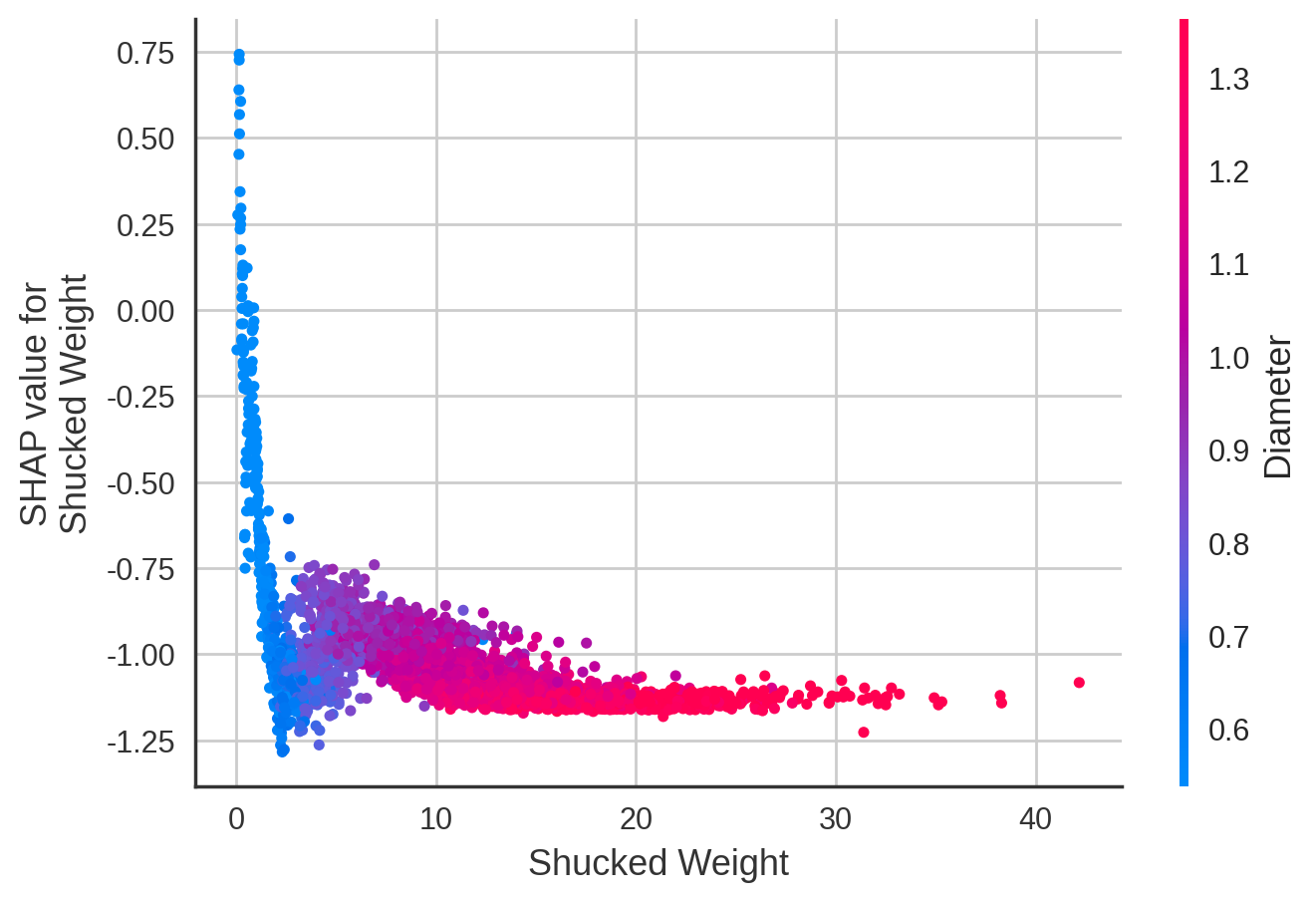
- 与
- 由上图可知:
- 与
Shucked Weight交互性最强的是Diameter - 当螃蟹不含壳的重量小于3时,重量越小,年龄越小。
- 去壳重量量越大,螃蟹直径越大
- 与
蜂群摘要图
- 蜂群图旨在显示数据集中的主要特征如何影响模型输出的信息密集摘要。
- 给定解释的每个实例都由每个特征流上的单个点表示。
- 点的 x 位置由该特征的 SHAP 值确定,点沿着每个特征行“堆积”以显示密度。颜色用于显示特征的原始值。
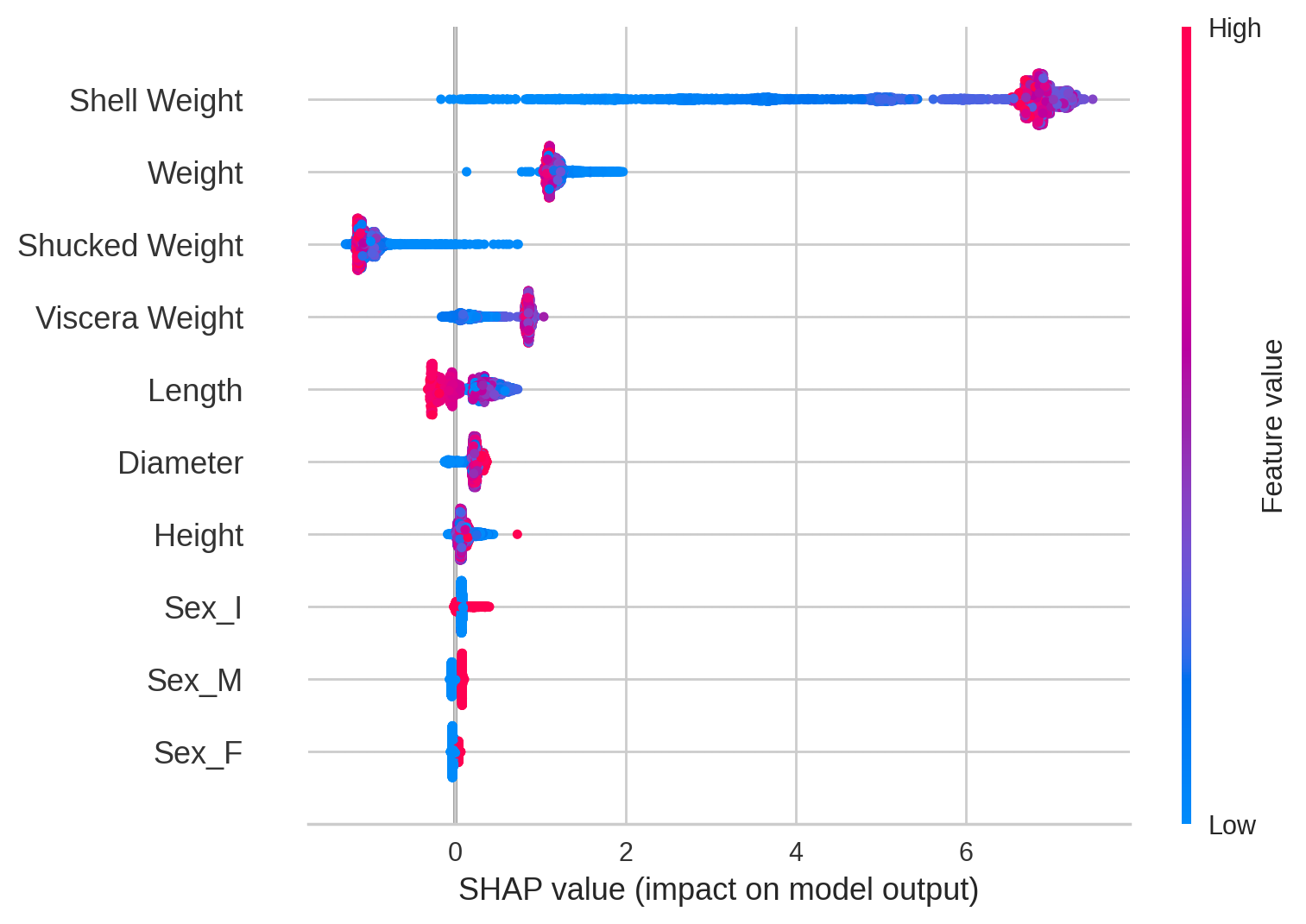
- 由上图可得以下结论:
- 平均而言外壳重量(
Sheel Weight)是最重要的特征,外壳重量越大,螃蟹年龄越大 - 不含壳重量(
Shucked Weight)越轻,反而可能有着更大的年龄。重的不含壳重量几乎年龄较小 - 长度(
Length)越长,年龄越小 - 直径(
Diameter)越小,几乎年龄较小 - 雄性(
Sex_M)和雌性(Sex_F),年龄相较于未知(Sex_I)更大
- 平均而言外壳重量(