上一篇博客介绍了BP神经网络遗传算法(BP-GA)函数极值寻优——非线性函数求极值，神经网络用的是BP神经网络，本篇博客将BP神经网络替换成GRNN神经网络，希望能帮助大家快速入门GRNN网络。

1.背景条件

要求：对于未知模型（函数表达式未知）求解极值。
条件：已知模型的一些输入输出数据。

程序的示例是根据用神经网络遗传算法寻优非线性函数 $y=x_1^2+x_2^2$ 的极值，输入参数有2个，输出参数有1个，易知函数有极小值0，极小值点为(0, 0)。已知的只有一些输入输出数据（用rand函数生成输入，然后代入表达式生成输出）：

for i=1:4000
    input(i,:)=10*rand(1,2)-5;
    output(i)=input(i,1)^2+input(i,2)^2;
end

2.GRNN神经网络函数说明

newgrnn

GRNN神经网络参数设置函数
函数形式：

net = newgrnn(P,T,spread)

P:输入数据矩阵。
T:输出数据矩阵。
spread：径向基函数的扩展速度。对GRNN网络来说，当确定了学习样本，则相应的网络结构和各神经元之间的连接权值也就确定出来，网络的训练实际上只是确定平滑参数的过程。GRNN网络中的即相当于径向基函数的分布密度SPREAD。一般情况下，SPREAD越大，逼近过程就越平滑，但误差也增大；SPREAD越小，函数逼近越精确，但逼近过程也越不平滑。

例如：

net=newgrnn(inputn,outputn,0.1)

GRNN神经网络和BP网络都可以用于预测，但对具体的网络训练来说，GRNN需要调整的参数较少，只有一个 spread 参数，因此可以更快地预测网络，具有较大的计算优势。

3.最优参数spread的确定

为了找到最优参数，可采用交叉验证的方法。

%% 清空环境变量
clc;
clear all
close all
nntwarn off;

%% 载入数据
load data;

%从1到4000间随机排序
k=rand(1,4000);
[m,n]=sort(k);
p_train=input(n(1:3900),:);
t_train=output(n(1:3900),:);
p_test=input(n(3901:4000),:);
t_test=output(n(3901:4000),:);

%% 交叉验证
desired_spread=[];
mse_max=10e20;
desired_input=[];
desired_output=[];
result_perfp=[];
indices = crossvalind('Kfold',length(p_train),4);
h=waitbar(0,'正在寻找最优化参数....')
k=1;
for i = 1:4
    perfp=[];
    disp(['以下为第',num2str(i),'次交叉验证结果'])
    test = (indices == i); train = ~test;
    p_cv_train=p_train(train,:);
    t_cv_train=t_train(train,:);
    p_cv_test=p_train(test,:);
    t_cv_test=t_train(test,:);
    p_cv_train=p_cv_train';
    t_cv_train=t_cv_train';
    p_cv_test= p_cv_test';
    t_cv_test= t_cv_test';
    [p_cv_train,minp,maxp,t_cv_train,mint,maxt]=premnmx(p_cv_train,t_cv_train);
    p_cv_test=tramnmx(p_cv_test,minp,maxp);
    for spread=0.1:0.1:2;
        net=newgrnn(p_cv_train,t_cv_train,spread);
        waitbar(k/80,h);
        disp(['当前spread值为', num2str(spread)]);
        test_Out=sim(net,p_cv_test);
        test_Out=postmnmx(test_Out,mint,maxt);
        error=t_cv_test-test_Out;
        disp(['当前网络的mse为',num2str(mse(error))])
        perfp=[perfp mse(error)];
        if mse(error)<mse_max
            mse_max=mse(error);
            desired_spread=spread;
            desired_input=p_cv_train;
            desired_output=t_cv_train;
        end
        k=k+1;
    end
    result_perfp(i,:)=perfp;
end;
close(h)
disp(['最佳spread值为',num2str(desired_spread)])
disp(['此时最佳输入值为'])
desired_input
disp(['此时最佳输出值为'])
desired_output
%% 采用最佳方法建立GRNN网络
net=newgrnn(desired_input,desired_output,desired_spread);
p_test=p_test';
p_test=tramnmx(p_test,minp,maxp);
grnn_prediction_result=sim(net,p_test);
grnn_prediction_result=postmnmx(grnn_prediction_result,mint,maxt);
grnn_error=t_test-grnn_prediction_result';
grnn_error=t_test-grnn_prediction_result;
disp('GRNN神经网络预测总误差为');
errorsum=sum(abs(grnn_error))
save best desired_input desired_output p_test t_test grnn_error mint maxt

运行之后得到：

最佳spread值为0.1

4.完整代码

data.m

用于生成神经网络拟合的原始数据。

for i=1:4000
    input(i,:)=10*rand(1,2)-5;
    output(i)=input(i,1)^2+input(i,2)^2;
end
output=output';

save data input output

GRNN.m

用函数输入输出数据训练GRNN神经网络，使训练后的网络能够拟合非线性函数输出，保存训练好的网络用于计算个体适应度值。根据非线性函数方程随机得到该函数的4000组输入输出数据，存储于data中，其中input为函数输入数据，output为函数对应输出数据，从中随机抽取3900组训练数据训练网络，100组测试数据测试网络拟合性能。最后保存训练好的网络。

%% 清空环境变量
clc;
tic

%% 载入数据
load data

%从1到4000间随机排序
k=rand(1,4000);
[m,n]=sort(k);

%找出训练数据和预测数据
p_train=input(n(1:3900),:)';
t_train=output(n(1:3900),:)';
p_test=input(n(3901:4000),:)';
t_test=output(n(3901:4000),:)';

[inputn,inputps]=mapminmax(p_train);
[outputn,outputps]=mapminmax(t_train);

%% 建立GRNN网络并训练验证
net=newgrnn(inputn,outputn,0.1); % 建立网络，spread的值可由交叉验证方法得出
inputn_test=mapminmax('apply',p_test,inputps); % 归一化
grnn_prediction_result=sim(net,inputn_test); % 验证网络
grnn_prediction_result=mapminmax('reverse',grnn_prediction_result,outputps); % 反归一化

%% 性能评估
grnn_error=t_test-grnn_prediction_result;
disp('GRNN神经网络预测总误差为');
errorsum=sum(abs(grnn_error))

figure(1);
plot(grnn_prediction_result,':og');
hold on
plot(t_test,'-*');
legend('Predictive output','Expected output','fontsize',10);
title('GRNN network predictive output','fontsize',12);
xlabel("samples",'fontsize',12);
ylabel('THD','fontsize',12);

figure(2);
plot(grnn_error,'-*');
title('Neural network prediction error');
xlabel("samples",'fontsize',12);

figure(3);
plot(100*(t_test-grnn_prediction_result)./grnn_prediction_result,'-*');
title('Neural network prediction error percentage (%)');
xlabel("samples",'fontsize',12);

toc

save data net inputps outputps

Code.m

编码成染色体。

function ret=Code(lenchrom,bound)
%本函数将变量编码成染色体，用于随机初始化一个种群
% lenchrom   input : 染色体长度
% bound      input : 变量的取值范围
% ret        output: 染色体的编码值
flag=0;
while flag==0
    pick=rand(1,length(lenchrom));
    ret=bound(:,1)'+(bound(:,2)-bound(:,1))'.*pick; %线性插值，编码结果以实数向量存入ret中
    flag=test(lenchrom,bound,ret);     %检验染色体的可行性
end

fun.m

把训练好的GRNN神经网络预测输出作为个体适应度值。

function fitness = fun(x)
% 函数功能：计算该个体对应适应度值
% x           input     个体
% fitness     output    个体适应度值

%
load data net inputps outputps

%数据归一化
x=x';
inputn_test=mapminmax('apply',x,inputps);
 
%网络预测输出
an=sim(net,inputn_test);
 
%网络输出反归一化
fitness=mapminmax('reverse',an,outputps);

对于求极小值的函数，适应度可以设为GRNN网络预测结果，如果需要求极大值，可以对适应度取反。

Select.m

选择操作采用轮盘赌法从种群中选择适应度好的个体组成新种群。

function ret=select(individuals,sizepop)
% 本函数对每一代种群中的染色体进行选择，以进行后面的交叉和变异
% individuals input  : 种群信息
% sizepop     input  : 种群规模
% ret         output : 经过选择后的种群

fitness1=1./individuals.fitness;
sumfitness=sum(fitness1);
sumf=fitness1./sumfitness;
index=[]; 
for i=1:sizepop   %转sizepop次轮盘
    pick=rand;
    while pick==0    
        pick=rand;        
    end
    for i=1:sizepop    
        pick=pick-sumf(i);        
        if pick<0        
            index=[index i];            
            break;  %寻找落入的区间，此次转轮盘选中了染色体i，注意：在转sizepop次轮盘的过程中，有可能会重复选择某些染色体
        end
    end
end
individuals.chrom=individuals.chrom(index,:);
individuals.fitness=individuals.fitness(index);
ret=individuals;

Cross.m

交叉操作从种群中选择两个个体，按一定概率交叉得到新个体。

function ret=Cross(pcross,lenchrom,chrom,sizepop,bound)
%本函数完成交叉操作
% pcorss                input  : 交叉概率
% lenchrom              input  : 染色体的长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% ret                   output : 交叉后的染色体
 for i=1:sizepop  %每一轮for循环中，可能会进行一次交叉操作，染色体是随机选择的，交叉位置也是随机选择的，%但该轮for循环中是否进行交叉操作则由交叉概率决定（continue控制）
     % 随机选择两个染色体进行交叉
     pick=rand(1,2);
     while prod(pick)==0
         pick=rand(1,2);
     end
     index=ceil(pick.*sizepop);
     % 交叉概率决定是否进行交叉
     pick=rand;
     while pick==0
         pick=rand;
     end
     if pick>pcross
         continue;
     end
     flag=0;
     while flag==0
         % 随机选择交叉位
         pick=rand;
         while pick==0
             pick=rand;
         end
         pos=ceil(pick.*sum(lenchrom)); %随机选择进行交叉的位置，即选择第几个变量进行交叉，注意：两个染色体交叉的位置相同
         pick=rand; %交叉开始
         v1=chrom(index(1),pos);
         v2=chrom(index(2),pos);
         chrom(index(1),pos)=pick*v2+(1-pick)*v1;
         chrom(index(2),pos)=pick*v1+(1-pick)*v2; %交叉结束
         flag1=test(lenchrom,bound,chrom(index(1),:));  %检验染色体1的可行性
         flag2=test(lenchrom,bound,chrom(index(2),:));  %检验染色体2的可行性
         if   flag1*flag2==0
             flag=0;
         else flag=1;
         end    %如果两个染色体不是都可行，则重新交叉
     end
 end
ret=chrom;

test.m

检验染色体的可行性。

function flag=test(lenchrom,bound,code)
% lenchrom   input : 染色体长度
% bound      input : 变量的取值范围
% code       output: 染色体的编码值

x=code; %先解码
flag=1;
if (x(1)<bound(1,1))&&(x(2)<bound(2,1))&&(x(1)>bound(1,2))&&(x(2)>bound(2,2))
    flag=0;
end

Mutation.m

变异操作从种群中随机选择一个个体，按一定概率变异得到新个体。

function ret=Mutation(pmutation,lenchrom,chrom,sizepop,pop,bound)
% 本函数完成变异操作
% pcorss                input  : 变异概率
% lenchrom              input  : 染色体长度
% chrom     input  : 染色体群
% sizepop               input  : 种群规模
% opts                  input  : 变异方法的选择
% pop                   input  : 当前种群的进化代数和最大的进化代数信息
% ret                   output : 变异后的染色体
for i=1:sizepop   %每一轮for循环中，可能会进行一次变异操作，染色体是随机选择的，变异位置也是随机选择的，
    %但该轮for循环中是否进行变异操作则由变异概率决定（continue控制）
    % 随机选择一个染色体进行变异
    pick=rand;
    while pick==0
        pick=rand;
    end
    index=ceil(pick*sizepop);
    % 变异概率决定该轮循环是否进行变异
    pick=rand;
    if pick>pmutation
        continue;
    end
    flag=0;
    while flag==0
        % 变异位置
        pick=rand;
        while pick==0      
            pick=rand;
        end
        pos=ceil(pick*sum(lenchrom));  %随机选择了染色体变异的位置，即选择了第pos个变量进行变异
        v=chrom(i,pos);        
        v1=v-bound(pos,1);        
        v2=bound(pos,2)-v;        
        pick=rand; %变异开始        
        if pick>0.5
            delta=v2*(1-pick^((1-pop(1)/pop(2))^2));
            chrom(i,pos)=v+delta;
        else
            delta=v1*(1-pick^((1-pop(1)/pop(2))^2));
            chrom(i,pos)=v-delta;
        end   %变异结束
        flag=test(lenchrom,bound,chrom(i,:));     %检验染色体的可行性
    end
end
ret=chrom;

Genetic.m

%% 清空环境变量
clc
% clear

%% 初始化遗传算法参数
%初始化参数
maxgen=100;                         %进化代数，即迭代次数
sizepop=20;                        %种群规模
pcross=[0.4];                       %交叉概率选择，0和1之间
pmutation=[0.2];                    %变异概率选择，0和1之间

lenchrom=[1 1];          %每个变量的字串长度，如果是浮点变量，则长度都为1
bound=[-5 5;-5 5];  %数据范围

individuals=struct('fitness',zeros(1,sizepop), 'chrom',[]);  %将种群信息定义为一个结构体
avgfitness=[];                      %每一代种群的平均适应度
bestfitness=[];                     %每一代种群的最佳适应度
bestchrom=[];                       %适应度最好的染色体

%% 初始化种群计算适应度值
% 初始化种群
for i=1:sizepop
    %随机产生一个种群
    individuals.chrom(i,:)=Code(lenchrom,bound);   
    x=individuals.chrom(i,:);
    %计算适应度
    individuals.fitness(i)=fun(x);   %染色体的适应度
end
%找最好的染色体
[bestfitness bestindex]=min(individuals.fitness);
bestchrom=individuals.chrom(bestindex,:);  %最好的染色体
avgfitness=sum(individuals.fitness)/sizepop; %染色体的平均适应度
% 记录每一代进化中最好的适应度和平均适应度
trace=[avgfitness bestfitness]; 

%% 迭代寻优
% 进化开始
for i=1:maxgen
    i
    % 选择
    individuals=Select(individuals,sizepop); 
    avgfitness=sum(individuals.fitness)/sizepop;
    % 交叉
    individuals.chrom=Cross(pcross,lenchrom,individuals.chrom,sizepop,bound);
    % 变异
    individuals.chrom=Mutation(pmutation,lenchrom,individuals.chrom,sizepop,[i maxgen],bound);
    
    % 计算适应度 
    for j=1:sizepop
        x=individuals.chrom(j,:); %解码
        individuals.fitness(j)=fun(x);   
    end
    
  %找到最小和最大适应度的染色体及它们在种群中的位置
    [newbestfitness,newbestindex]=min(individuals.fitness);
    [worestfitness,worestindex]=max(individuals.fitness);
    % 代替上一次进化中最好的染色体
    if bestfitness>newbestfitness
        bestfitness=newbestfitness;
        bestchrom=individuals.chrom(newbestindex,:);
    end
    individuals.chrom(worestindex,:)=bestchrom;
    individuals.fitness(worestindex)=bestfitness;
    
    avgfitness=sum(individuals.fitness)/sizepop;
    
    trace=[trace;avgfitness bestfitness]; %记录每一代进化中最好的适应度和平均适应度
end
%进化结束

%% 结果分析
[r c]=size(trace);
plot([1:r]',trace(:,2),'r-');
title('适应度曲线','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
axis([0,100,0,1])
disp('适应度                   变量');
x=bestchrom;
% 窗口显示
disp([bestfitness x]);

5.代码使用说明

上述代码运行顺序

data.m 生成数据（如果已有 input output 数据可跳过），
GRNN.m 进行GRNN神经网络训练及函数拟合，
Genetic.m（主函数）利用遗传算法求极值。

求最大值的方法

上述代码用于求解最小值，对于求解最大值的需求，可以在适应度函数里面，对适应度计算结果求反，把求解最大值的问题转化为求解最小值的问题。

例如：对于非线性函数 $y=-(x_1^2+x_2^2)+4$ ：

for i=1:4000
    input(i,:)=10*rand(1,2)-5;
    output(i)=-(input(i,1)^2+input(i,2)^2)+4;
end

求最大值时，需要在 fun.m 里面，修改最后一行代码：

fitness=-mapminmax('reverse',an,outputps);

最终运行找到的极值点为（0.4714， -0.0319），适应度为-3.7554，极值需要对适应度取反，为3.7554。

注意：每次运行结果不尽相同。

6.代码运行结果

对 $y=x_1^2+x_2^2$ 求极小值

GRNN神经网络拟合

运行GRNN.m之后：

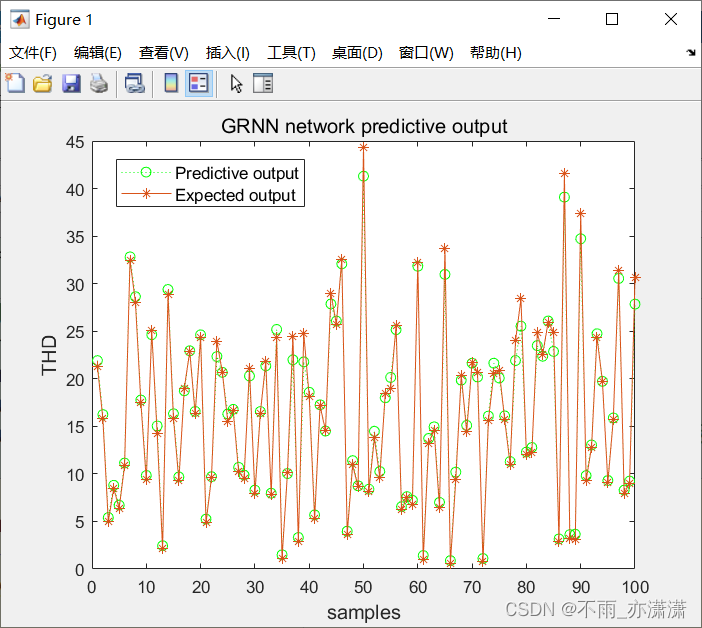
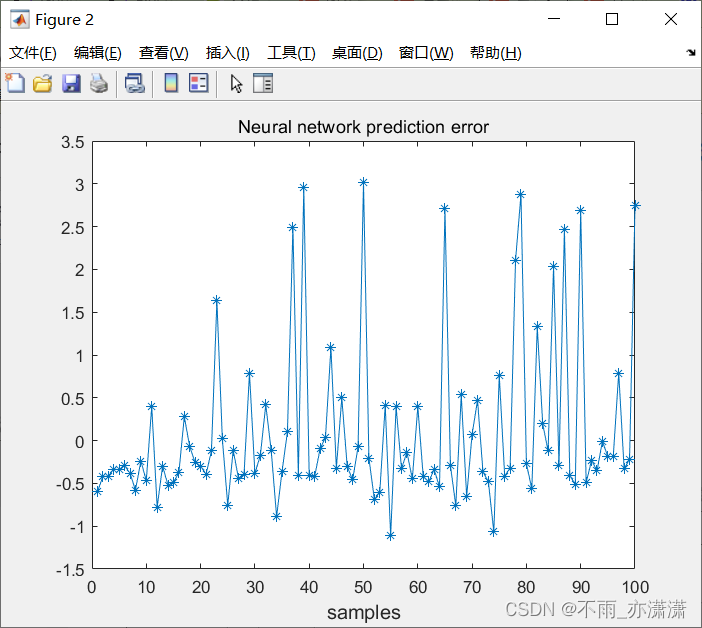
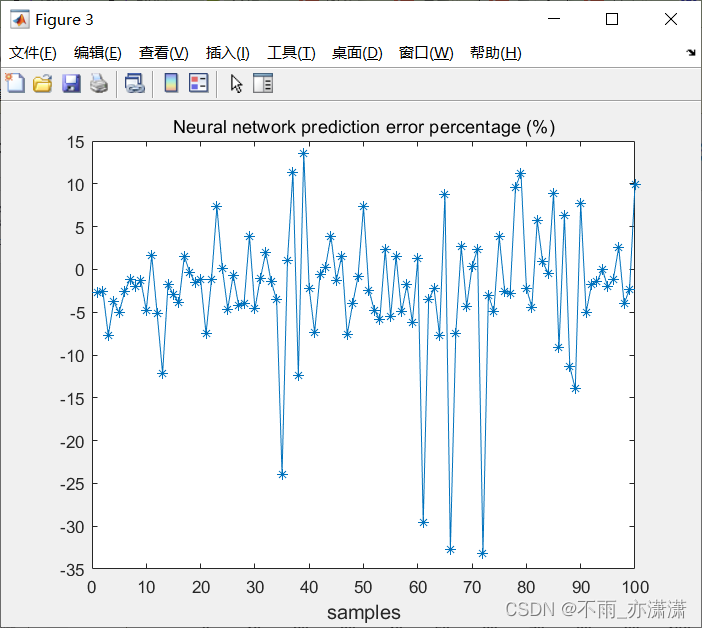
输出：

errorsum =

    64.3379

历时 0.511482 秒。

注意：每次运行结果不尽相同。

遗传算法寻优

运行主函数 Genetic.m之后：

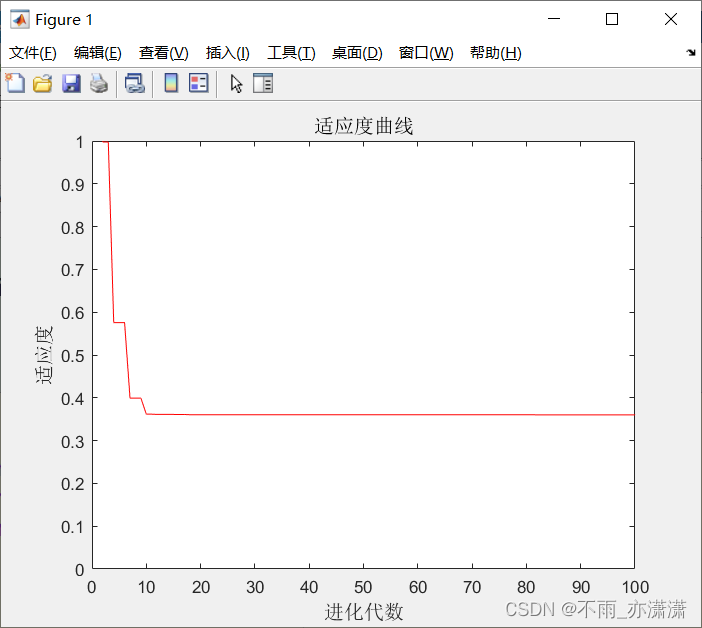
输出：

...
i =

   100

适应度                   变量
    0.3600    0.0066    0.0117

最终结果最优个体为（0.0066，0.0117），适应度为 0.3600。

注意：每次运行结果不尽相同。

参考

《MATLAB神经网络30个案例分析》