概述

IOU的出现主要最先运用在预测bbox框和target bbox框之间的重叠问题，为NMS提供相应的数值支撑。另外在bbox框的回归问题上，由于L1 Loss存在如下问题：当损失函数对x的导数为常数，在训练后期，x很小时，若学习率不变，损失函数会在稳定值附近波动，很难收敛到更高的精度。而L2 Loss存在如下问题：当损失函数对x的导数在x值很大时，其导数也非常大，在训练初期不稳定。L1/L2 Loss的坐标回归不具有尺度不变性，且没有将四个坐标之间的相关性考虑进去。因此，基于L1/L2 Loss的坐标回归实际上很难描述两框之间的相对位置关系。

而IOU天然是衡量两个bbox框之间的重叠程度，以自身四个点作为回归对象，具备尺度不变性。实际计算中通常以1-IOU作为loss，主要是当框的重合度特别高的时候，需要的惩罚相对较少，而当两个框重合度较低时，需要的惩罚就相对比较大。IOU的取值范围为【0，1】，当两者完全重合时，loss为0，当两者完全不重合时，取值为0。

从上面概述也能够了解，IOU作为loss在优化过程中必然会存在一些问题，比如两者不相交，无法产生梯度，再比如两者相互包含，但是位置不同如何继续快速优化等等的问题，这些问题都会归于：重叠比例、长宽比例、中心点比例等等，因此IOU发展史必然就是一个发现问题，解决问题，然后再发现再解决的过程。下面不妨随我一道走马观花，看看IOU的发展。

1、IOU

论文地址：https://arxiv.org/abs/1608.01471

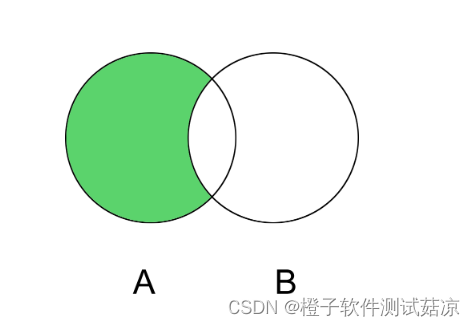
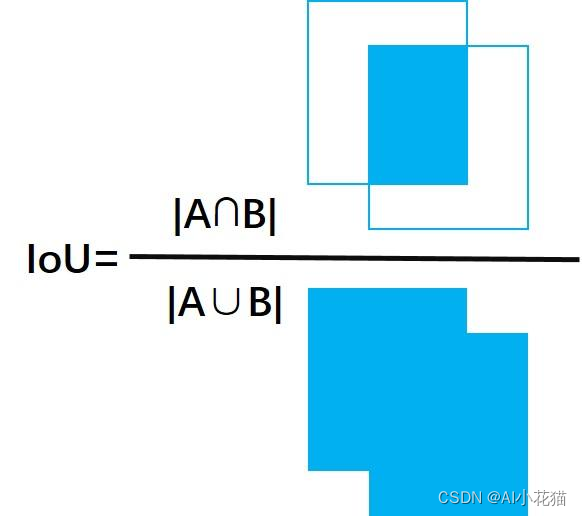
IOU时用于衡量两个bbox框的重叠程度，那么具体是如何衡量的了？直观上来讲就是【交并比】，实际情况就如下图所示，A和B的交集是两个bbox框的蓝色交叠部分，A和B的并集是两个bbox框的所有合并部分，A和B交集和并集的比值就是我们所谓的IOU。

IOU作为坐标回归的loss函数，具有如下三个优点：

• 尺度不变性
• 非负性
• 对称性
  

但是它存在一定的问题：

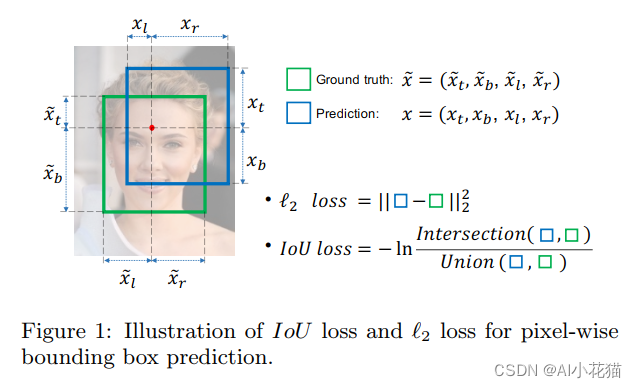
• 两个框没有相交时，无法比较框的距离远近，不相交的两个框也不会产生梯度，无法优化；
• IoU无法区分两个框之间不同的对齐方式。更确切地讲，不同方向上有相同交叉级别的两个重叠对象的IoU会完全相等。
  

IOU的实现方式比较简单，具体实现代码如下：

def iou(bbox1, bbox2, eps=1e-8):
    """
    :param bbox1:  [x1y1x2y2]
    :param bbox2:  [x1y1x2y2]
    :return:
    """
    # insertion
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    area_1 = (bbox1[2] - bbox1[0]) * (bbox1[3] - bbox1[1])
    area_2 = (bbox2[2] - bbox2[0]) * (bbox2[3] - bbox2[1])
    area_union = area_1 + area_2 - w_insert * h_insert + eps
    iou_val = float(w_insert * h_insert) / area_union
    return iou_val

论文中关于IOU LOSS的实现算法如下图所示，实际上就是-ln(IOU),实际运用中都是使用1-IOU来代替IOU loss。

2、GIOU

论文地址：https://arxiv.org/abs/1902.09630

IOU loss出现两个框没有交集无法进行梯度回传的情况，GIOU的出现主要就是解决这个问题。
那GIOU是怎么定义的了？

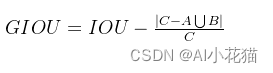
其中C是bbox框A和B的最小外接矩形的面积
从公式来看，考虑了两个bbox框最小外接矩形除去交集以外的部分，使得GIOU的取值范围为【-1，1】，当A和B没有交集且相距无限远的时候，GIOU为-1，而当两者完全重合的时候，GIOU和IOU一样都为1。

论文中实现的方法如下：

GIOU相对于IOU的改进：

• 相对于IOU来说只关注重叠区域，GIOU不仅关注重叠区域还关注非重叠区域，这样的好处是可以解决两个bbox框没有交集时仍然有梯度回传，可以继续进行优化。
• 完善了两个bbox框的重叠区域优化

仍然存在的问题：

• GIOU没有考虑长宽比、中心距离等信息，会导致两个bbox框相互包含时，虽然IOU或者GIOU相同，但是却位置上却不尽相同，无法找到更好的优化方向

按照上面的GIOU的公式，使用python复现，具体实现代码如下：

def Giou(bbox1, bbox2, eps=1e-8):
 ## 解决的问题是预测框和目标狂不重合，梯度为0， 无法进行优化的问题
   """
    :param bbox1:  [x1y1x2y2]
    :param bbox2:  [x1y1x2y2]
    :return:
    """
    # insertion
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    area_1 = (bbox1[2] - bbox1[0]) * (bbox1[3] - bbox1[1])
    area_2 = (bbox2[2] - bbox2[0]) * (bbox2[3] - bbox2[1])
    area_union = area_1 + area_2 - w_insert * h_insert + eps

    # enclosing area
    enclose_left = min(bbox1[0], bbox2[0])
    enclose_top = min(bbox1[1], bbox2[1])
    enclose_right = max(bbox1[2], bbox2[2])
    enclose_bottom = max(bbox1[3], bbox2[3])

    enclose = max(0, enclose_right - enclose_left) * max(0, enclose_bottom - enclose_top) + eps
    iou_val = float(w_insert * h_insert) / area_union
    giou_val = iou_val - (enclose - area_union) / enclose
    return giou_val

3、DIOU

论文地址：https://arxiv.org/abs/1911.08287

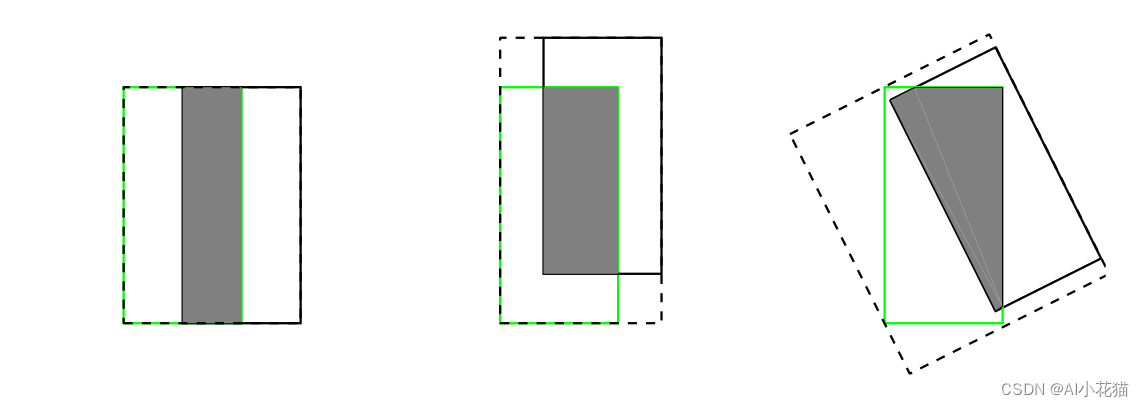
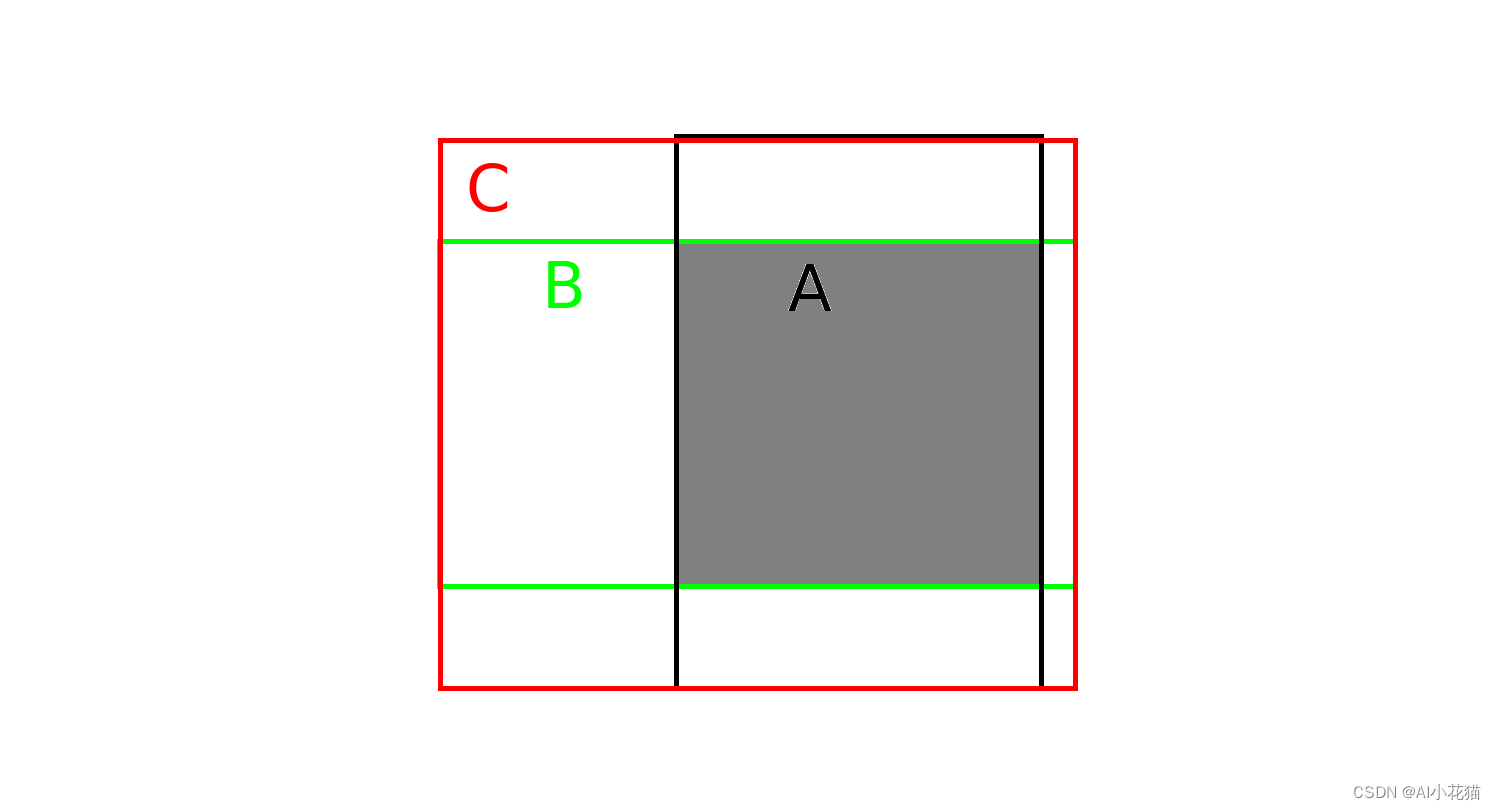
IOU作为边框回归的Loss函数主要考虑的三点因素为：重叠面积、中心点距离、长宽比等，重叠面积实际上在IOU和GIOU中予以充分考虑了。但仅考虑重叠面积会存在问题：当预测框和真是框之间存在包含关系的时，不同位置的IOU和GIOU都是相同的（此时GIOU已经退化为IOU了），因此仅仅考虑重叠面积已经无法继续优化，具体的情况去下所示：

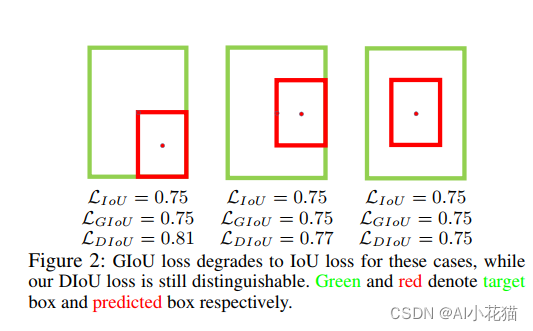
DIOU Loss的计算公式如下所，相对于IOU本身来说，主要考虑了预测框和真实框中心点之间的距离和最小包围框之间的距离。


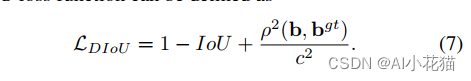
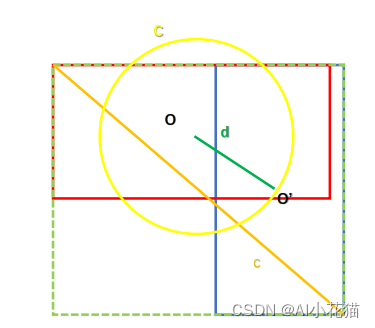
DIoU的特点如下：

• DIOU与IOU、GIOU一样具有尺度不变性
• DIOU与GIOU一样在与目标框不重叠时，仍然可以为边界框提供移动方向
• DIOU可以直接最小化两个目标框的距离，因此比GIOU Loss收敛快得多
• DIOU在包含两个框水平/垂直方向上的情况回归很快，而GIOU几乎退化为IOU
• 当预测框和真实框完全重叠，DIOU Loss为0

DIOU的具体实现代码如下所示：

def Diou(bbox1, bbox2, eps=1e-8):
    # 主要解决预测框和真实框具有包含关系时候，Giou失效问题，考虑了重叠面积和中心点距离
     """
    :param bbox1:  [x1y1x2y2]
    :param bbox2:  [x1y1x2y2]
    :return:
    """
    # insertion
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    area_1 = (bbox1[2] - bbox1[0]) * (bbox1[3] - bbox1[1])
    area_2 = (bbox2[2] - bbox2[0]) * (bbox2[3] - bbox2[1])
    area_union = area_1 + area_2 - w_insert * h_insert + eps

    # enclosing coord
    enclose_left = min(bbox1[0], bbox2[0])
    enclose_top = min(bbox1[1], bbox2[1])
    enclose_right = max(bbox1[2], bbox2[2])
    enclose_bottom = max(bbox1[3], bbox2[3])
    enclose_distance = math.pow((enclose_right - enclose_left), 2) + math.pow((enclose_bottom - enclose_top), 2) + eps
    # bbox center
    cx1 = (bbox1[0] + bbox1[2]) / 2.0
    cy1 = (bbox1[1] + bbox1[3]) / 2.0
    cx2 = (bbox2[0] + bbox2[2]) / 2.0
    cy2 = (bbox2[1] + bbox2[3]) / 2.0
    center_distance = math.pow((cx2 - cx1), 2) + math.pow((cy2 - cy1), 2)
    iou_val = float(w_insert * h_insert) / area_union
    doiu_val = iou_val - float(center_distance) / enclose_distance
    return doiu_val

存在问题：
虽然DIOU能够直接最小化预测框和真实框的中心点距离加速收敛，但是Bounding box的回归还有一个重要的因素纵横比暂未考虑

4、CIoU

论文地址：https://arxiv.org/abs/2103.11696

CIOU Loss 和 DIOU Loss出自同一篇文章，CIOU在DIOU的基础上将Bounding box的纵横比考虑进损失函数中，进一步提升了回归精度。

CIoU Loss的计算公式如下所示：

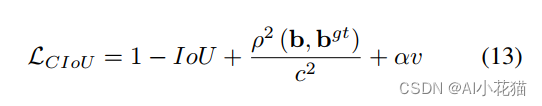
相对于DIoU来说，只是对增加了一项alpha和V，其具体计算方式如下：

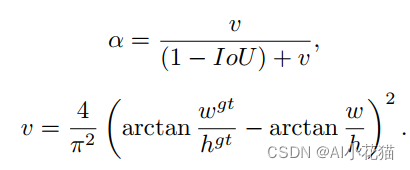
CIou的具体实现代码如下：

def Ciou(bbox1, bbox2, eps=1e-8):
    # 在DIOU上面做优化，考虑了中心距离、重叠面积、长宽比
    # insertion
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    w1 = bbox1[2] - bbox1[0]
    h1 = bbox1[3] - bbox1[1]
    w2 = bbox2[2] - bbox2[0]
    h2 = bbox2[3] - bbox2[1]
    area_1 = w1 * h1
    area_2 = w2 * h2
    area_union = area_1 + area_2 - w_insert * h_insert + eps

    # enclosing coord
    enclose_left = min(bbox1[0], bbox2[0])
    enclose_top = min(bbox1[1], bbox2[1])
    enclose_right = max(bbox1[2], bbox2[2])
    enclose_bottom = max(bbox1[3], bbox2[3])
    enclose_distance = math.pow((enclose_right - enclose_left), 2) + math.pow((enclose_bottom - enclose_top), 2) + eps
    # bbox center
    cx1 = (bbox1[0] + bbox1[2]) / 2.0
    cy1 = (bbox1[1] + bbox1[3]) / 2.0
    cx2 = (bbox2[0] + bbox2[2]) / 2.0
    cy2 = (bbox2[1] + bbox2[3]) / 2.0
    center_distance = math.pow((cx2 - cx1), 2) + math.pow((cy2 - cy1), 2)

    iou_val = float(w_insert * h_insert) / area_union

    # av
    v = 4 / math.pi * math.pow((math.atan(w1 / (h1 + eps)) - math.atan(w2 / (h2 + eps))), 2)
    alfa = v / ((1 - iou_val) + v + eps)

    coiu_val = iou_val - float(center_distance) / enclose_distance - alfa * v
    return coiu_val

存在的问题：
纵横比权重的设计还需要继续优化，以获取更好的方案。

5、EIoU

论文地址：https://arxiv.org/abs/2101.08158

CIOU Loss虽然考虑了边界框回归的重叠面积、中心点距离、纵横比。但是通过其公式中的v反映的是纵横比的差异，而非宽高分别与其置信度的真实差异。因此作者在原始CIoU的基础上改进纵横比的情况得到了EIoU，并考虑到框的样本不均衡性，使用了类Focal Loss的设计方式，得到了Focal-EIoU。

EIoU Loss的具体计算公式如下：

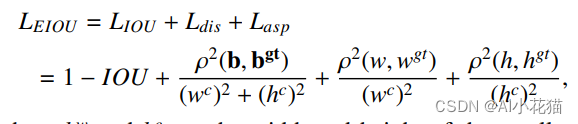
EIOU具体实现代码如下：

def Eiou(bbox1, bbox2, eps=1e-8):
    # insertion
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    w1 = bbox1[2] - bbox1[0]
    h1 = bbox1[3] - bbox1[1]
    w2 = bbox2[2] - bbox2[0]
    h2 = bbox2[3] - bbox2[1]
    area_1 = w1 * h1
    area_2 = w2 * h2
    area_union = area_1 + area_2 - w_insert * h_insert + eps

    # enclosing coord
    enclose_left = min(bbox1[0], bbox2[0])
    enclose_top = min(bbox1[1], bbox2[1])
    enclose_right = max(bbox1[2], bbox2[2])
    enclose_bottom = max(bbox1[3], bbox2[3])
    enclose_distance = math.pow((enclose_right - enclose_left), 2) + math.pow((enclose_bottom - enclose_top), 2) + eps
    # bbox center
    cx1 = (bbox1[0] + bbox1[2]) / 2.0
    cy1 = (bbox1[1] + bbox1[3]) / 2.0
    cx2 = (bbox2[0] + bbox2[2]) / 2.0
    cy2 = (bbox2[1] + bbox2[3]) / 2.0
    center_distance = math.pow((cx2 - cx1), 2) + math.pow((cy2 - cy1), 2)

    iou_val = float(w_insert * h_insert) / area_union

    # cw ch w-wgt h-hgt
    cw = enclose_right - enclose_left
    ch = enclose_bottom - enclose_top
    w_distance = math.pow((w1 - w2), 2)
    h_distance = math.pow((h1 - h2), 2)

    eiou_val = iou_val - float(center_distance) / enclose_distance - w_distance / (
            math.pow(cw, 2) + eps) - h_distance / (math.pow(ch, 2) + eps)
    return eiou_val

6、αIoU

论文地址：https://arxiv.org/abs/2110.13675

作者将现有的基于IoU Loss推广到一个新的Power IoU系列 Loss，该系列具有一个Power IoU项和一个附加的Power正则项，具有单个Power参数α，称这种新的损失系列为α-IoU Loss。

该文章主要的贡献如下：

• 提出了一种新的power IoU损失函数，称为α-IoU，用于精确的bbox回归和目标检测。α-IoU是基于IoU的现有损失的统一幂化；
• 分析了α-IoU的一系列性质，包括顺序保留和损失/梯度重加权，表明适当选择α(即α > 1)有助于提高High IoU目标的损失和梯度自适应加权的bbox回归精度；
• 经验表明，在多个目标检测数据集和模型上，α-IoU损失优于现有的基于IoU的损失，并为小数据集和噪声Box提供更强的鲁棒性。

αIoU设计如下所示：

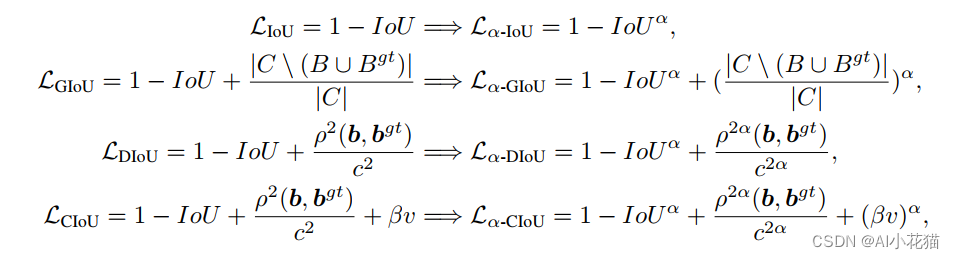
αIoU具体实现代码如下：

def alfa_iou(bbox1, bbox2, eps=1e-8, alfa=1, iou_type='iou'):
    assert iou_type in ['iou', 'giou', 'diou', 'ciou', 'eiou'], 'iou_type is not in the vanlid range type'
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    w1 = bbox1[2] - bbox1[0]
    h1 = bbox1[3] - bbox1[1]
    w2 = bbox2[2] - bbox2[0]
    h2 = bbox2[3] - bbox2[1]
    area_1 = w1 * h1
    area_2 = w2 * h2
    area_union = area_1 + area_2 - w_insert * h_insert + eps
    if iou_type in ['iou']:
        iou_val_alfa = math.pow(float(w_insert * h_insert) / area_union, alfa)
        return iou_val_alfa

    # enclosing coord
    enclose_left = min(bbox1[0], bbox2[0])
    enclose_top = min(bbox1[1], bbox2[1])
    enclose_right = max(bbox1[2], bbox2[2])
    enclose_bottom = max(bbox1[3], bbox2[3])
    if iou_type in ['giou']:
        enclose = max(0, enclose_right - enclose_left) * max(0, enclose_bottom - enclose_top) + eps
        iou_val = float(w_insert * h_insert) / area_union
        iou_val_alfa = math.pow(iou_val, alfa) - math.pow((enclose - area_union) / enclose, alfa)

    if iou_type in ['diou', 'ciou', 'eiou']:
        # bbox center
        cx1 = (bbox1[0] + bbox1[2]) / 2.0
        cy1 = (bbox1[1] + bbox1[3]) / 2.0
        cx2 = (bbox2[0] + bbox2[2]) / 2.0
        cy2 = (bbox2[1] + bbox2[3]) / 2.0
        center_distance = math.pow((cx2 - cx1), 2 * alfa) + math.pow((cy2 - cy1), 2 * alfa)
        enclose_distance = math.pow((enclose_right - enclose_left), 2 * alfa) + math.pow((enclose_bottom - enclose_top),
                                                                                         2 * alfa) + eps
        iou_val = float(w_insert * h_insert) / area_union
        if iou_type in ['diou']:
            iou_val_alfa = math.pow(iou_val, alfa) - float(center_distance) / enclose_distance

        elif iou_type in ['ciou']:
            # av
            v = 4 / math.pi * math.pow((math.atan(w1 / (h1 + eps)) - math.atan(w2 / (h2 + eps))), 2)
            alfa2 = v / ((1 - iou_val) + v + eps)
            iou_val_alfa = math.pow(iou_val, alfa) - float(center_distance) / enclose_distance - math.pow(alfa2 * v,
                                                                                                          alfa)
        else:  ## eiou
            # cw ch w-wgt h-hgt
            cw = enclose_right - enclose_left
            ch = enclose_bottom - enclose_top
            w_distance = math.pow((w1 - w2), 2 * alfa)
            h_distance = math.pow((h1 - h2), 2 * alfa)
            iou_val_alfa = math.pow(iou_val, alfa) - float(center_distance) / enclose_distance - w_distance / (
                    math.pow(cw, 2 * alfa) + eps) - h_distance / (math.pow(ch, 2 * alfa) + eps)
    return iou_val_alfa

7、SIoU

论文地址：https://arxiv.org/abs/2205.12740

传统的目标检测损失函数依赖于边界框回归的度量集合，如距离、重叠面积和纵横比预测和真实框的比率，迄今为止提出和使用的方法都没有考虑到真实框与预测框之间不匹配的方向。这种不足导致更慢和更少有效的收敛，因为预测框可能在训练过程中“徘徊”，并且最终会产生更差的模型，SIou的提出正好是解决这个问题。

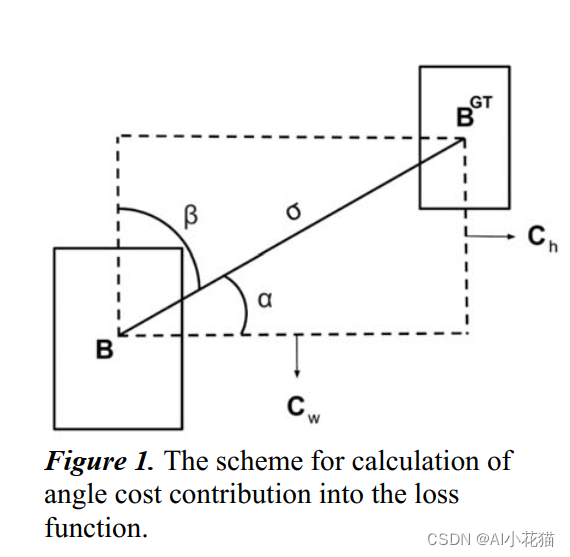
SIoU损失函数要考虑4方面的损失：

• Angle cost
  

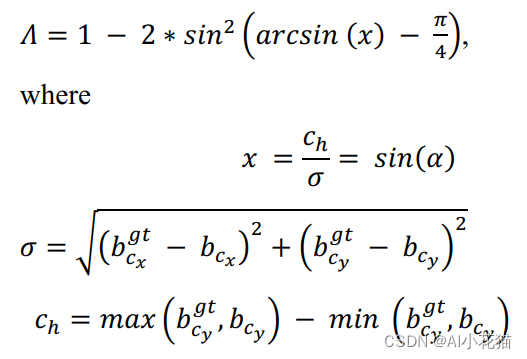
• Distance cost
  

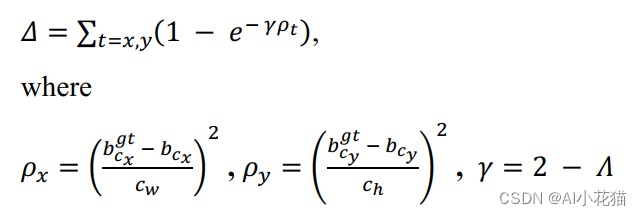
• Shape cost
  

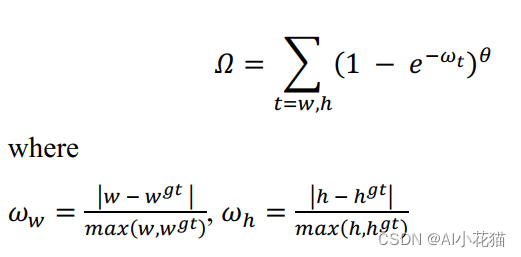
• IoU cost
  
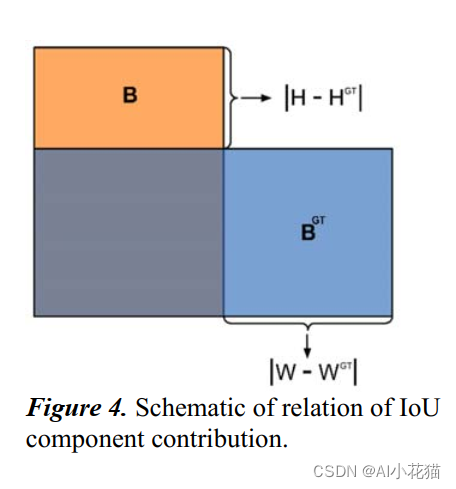
  最终Siou Loss的定义如下：
  

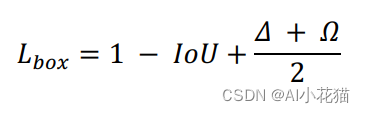
SIoU具体实现代码如下：

def Siou(bbox1, bbox2, eps=1e-8, threta=4):
    ## 参考美团实现
    # insertion
    left = max(bbox1[0], bbox2[0])
    top = max(bbox1[1], bbox2[1])
    right = min(bbox1[2], bbox2[2])
    bottom = min(bbox1[3], bbox2[3])
    w_insert = max(0, right - left)
    h_insert = max(0, bottom - top)
    # union
    w1 = bbox1[2] - bbox1[0]
    h1 = bbox1[3] - bbox1[1]
    w2 = bbox2[2] - bbox2[0]
    h2 = bbox2[3] - bbox2[1]
    area_1 = w1 * h1
    area_2 = w2 * h2
    area_union = area_1 + area_2 - w_insert * h_insert + eps
    iou_val = float(w_insert * h_insert) / area_union

    # enclosing coord
    enclose_left = min(bbox1[0], bbox2[0])
    enclose_top = min(bbox1[1], bbox2[1])
    enclose_right = max(bbox1[2], bbox2[2])
    enclose_bottom = max(bbox1[3], bbox2[3])
    cw = enclose_right - enclose_left
    ch = enclose_bottom - enclose_top

    # bbox center
    cx1 = (bbox1[0] + bbox1[2]) / 2.0
    cy1 = (bbox1[1] + bbox1[3]) / 2.0
    cx2 = (bbox2[0] + bbox2[2]) / 2.0
    cy2 = (bbox2[1] + bbox2[3]) / 2.0
    sigma = math.pow((cx2 - cx1), 2) + math.pow((cy2 - cy1), 0.5)

    sin_alpha_1 = math.fabs(cx2 - cx1) / sigma
    sin_alpha_2 = math.fabs(cy2 - cy1) / sigma

    threshold = math.pow(2, 0.5) / 2
    sin_alpha = sin_alpha_2 if sin_alpha_1 > threshold else sin_alpha_1
    angle_cost = math.cos(math.asin(sin_alpha) * 2 - math.pi / 2)  ### 1-sin(x)^2 = cos(2x)
    rho_x = math.pow((cx2 - cx1) / cw, 2)
    rho_y = math.pow((cy2 - cy1) / ch, 2)
    gamma = angle_cost - 2
    distance_cost = 2 - math.exp(gamma * rho_x) - math.exp(gamma * rho_y)
    omiga_w = math.fabs(w1 - w2) / max(w1, w2)
    omiga_h = math.fabs(h1 - h2) / max(h1, h2)
    shape_cost = math.pow(1 - math.exp(-omiga_w), threta) + math.pow(1 - math.exp(-omiga_h), threta)
    siou = iou_val - 0.5 * (distance_cost + shape_cost)
    return siou

8、Wise-IOU

论文地址：https://arxiv.org/abs/2301.10051
作者导读：Wise-IoU 作者导读：基于动态非单调聚焦机制的边界框损失

参考
https://zhuanlan.zhihu.com/p/452207890
https://zhuanlan.zhihu.com/p/270663039
https://blog.csdn.net/amusi1994/article/details/125176515