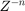[ABC218G] Game on Tree 2 树上游戏

文章目录

[ABC218G] Game on Tree 2 树上游戏
- 题面翻译
- 输入格式
- 输出格式
- 样例 #1
- - 样例输入 #1
  - 样例输出 #1
- 样例 #2
- - 样例输入 #2
  - 样例输出 #2
- 样例 #3
- - 样例输入 #3
  - 样例输出 #3
- 题目大意
- 分析
- - 水法
  - - code
  - 正解
  - - code

题面翻译

给定一棵树，以及树各节点的点权（点权为偶数）。起初有一个棋子在树的根结点（结点 $1$ ）处。

$A$ 与 $B$ 两人轮流操作：将棋子移动到其所在节点的某个叶子节点。
到某个节点的得分定义为：棋子经过所有结点点权的中位数。 $K$ 个数的中位数定义如下：
- 当 $K$ 为奇数时，中位数为 $K$ 个数中第 $\frac{K+1}{2}$ 小的值。
- 当 $K$ 为偶数时，中位数为 $K$ 个数中第 $\frac{K}{2}$ 小与第 $\frac{K}{2}+1$ 小的两数的平均值。
$A$ 希望最后得分尽可能大， $B$ 希望最后得分尽可能小。
当棋子到达某个叶节点时，游戏结束。

若 $A$ 先手操作， $A$ ， $B$ 都采取最优策略，求最终得分。

输入格式

入力は以下の形式で標準入力から与えられる。

$ N $ $ A_1 $ $ A_2 $ $ \ldots $ $ A_N $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_{N-1} $ $ v_{N-1} $

输出格式

両者が最適に行動するとき、駒が訪れた頂点に書かれた数の（多重）集合の中央値を出力せよ。

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

6
2 2 6 4 6 6
1 2
2 3
4 6
2 5
2 6

样例输出 #3

题目大意

一棵树上有 $n$ 个点，每个点有一个点值。在顶点1处有一块令牌，现在小T和小J开始玩游戏，它们轮流移动令牌到一个邻接点，令牌不能两次经过同一个点，最后令牌不能移动为止。令牌移动过程中经过的点，将它们的权值加入一个数组，求该数组的中位数。注意：小T移动时，他会采取最佳策略使得最终的中位数最大，而小J刚好相反，他会使得最终中位数最小。两个人都按照最佳策略去移动令牌。问最后的中位数是多少。

分析

水法

考试时用了5分钟打了一个贪心的做法，就是每次最优策略只考虑下一层的情况，居然拿到了67分的好成绩。

code

#include <bits/stdc++.h>
#define fu(x, y, z) for (int x = y; x <= z; x++)
using namespace std;
const int N = 1e5 + 5;
int n, cnt, hd[N], a[N], ans[N], sum, fa[N];
struct node {
    int to, nt;
} e[N << 1];
void add(int u, int v) { e[++cnt].to = v, e[cnt].nt = hd[u], hd[u] = cnt; }
void dfs(int x, int y) {
    int flg = 0, max1 = 0, min1 = 1e9 + 5, v, j, k;
    for (int i = hd[x]; i; i = e[i].nt) {
        v = e[i].to;
        if (fa[x] == v)
            continue;
        flg = 1;
        if (max1 < a[v])
            max1 = a[v], j = v;
        if (min1 > a[v])
            min1 = a[v], k = v;
    }
    if (!flg)
        return;
    if (y) {
        fa[j] = x;
        ans[++sum] = a[j];
        dfs(j, y ^ 1);
    } else {
        fa[k] = x;
        ans[++sum] = a[k];
        dfs(k, y ^ 1);
    }
}
void solve() {
    sort(ans + 1, ans + sum + 1);
    if (sum % 2 == 1)
        printf("%d", ans[sum / 2 + 1]);
    else
        printf("%d", ans[sum / 2] + ans[sum / 2 + 1] >> 1);
}
int main() {
    scanf("%d", &n);
    fu(i, 1, n) scanf("%d", &a[i]);
    int u, v;
    fu(i, 1, n - 1) {
        scanf("%d%d", &u, &v);
        add(u, v), add(v, u);
    }
    ans[++sum] = a[1];
    dfs(1, 1);
    solve();
}

正解

观察一下我们可以发现，每个叶子节点代表一条路径，我们可以先用 $D FS$ 统计出每个叶子结点的路径，并求出中位数，然后模拟。

~~好像会超时~~

我们发现可以用两个 multiset 或者对顶堆来维护这一条路径。

对顶堆 不会的可以看一下这个

如果两个 $m u lt i se t$ 长度相等，那么中位数就是第一个数列加上第二个数列再除以二

否则就是第一个数列的最后一个数。

code

#include <bits/stdc++.h>
#define fu(x , y , z) for(int x = y ; x <= z ; x ++)
#define LL long long
using namespace std;
const int N = 1e5 + 5;
int n , cnt , hd[N] , a[N] , sum , fa[N] , max1[N] , min1[N] , ans1 , f[N] , ans[N];
struct node {
    int to , nt;
} e[N << 1];
multiset<int> s1 , s2;
void add (int u , int v) { e[++cnt].to = v , e[cnt].nt = hd[u] , hd[u] = cnt; }
void dfs (int x , int fa) {
    bool flg = 0;
    if (x == 1) s1.insert(a[x]);
    else {
        auto t = s1.end();
        t --;
        if (a[x] <= *t) {
            if (s1.size() == s2.size()) s1.insert(a[x]);
            else {
                s1.insert(a[x]);
                auto y = s1.end();
                y --;
                s2.insert(*y) , s1.erase(y);
            }
        } 
        else {
            if (s1.size() == s2.size()) {
                s2.insert(a[x]);
                auto y = s2.begin();
                s1.insert(*y) , s2.erase(y);
            }
            else s2.insert(a[x]);
        }
    }
    for (int i = hd[x] ; i ; i = e[i].nt) {
        if (e[i].to == fa) continue;
        flg = 1;
        dfs (e[i].to , x);
    }
    if (!flg) {
        int len = s1.size() + s2.size();
        if (len & 1) {
            auto t = s1.end();
            t --;
            f[x] = *t;
        }
        else {
            auto a = s1.end();
            a--;
            auto b = s2.begin();
            f[x] = *a + *b >> 1;
        }
    }
    if (x != 1) {
        auto t = s1.end ();
        t --;
        if (*t < a[x]) s2.erase(s2.lower_bound(a[x]));
        else s1.erase(s1.lower_bound(a[x]));
        if (s1.size() < s2.size()) {
            auto y = s2.begin();
            s1.insert(*y) , s2.erase(y);
        }
        if (s1.size() - s2.size() == 2) {
            auto y = s1.end();
            y --;
            s2.insert(*y) , s1.erase(y);
        }
    }
}
void solve (int x , int fa , int flg) {
    int res;
    if (!flg)  res = -1;
    else res = 1e9 + 5;
    int y , bl = 0;
    for (int i = hd[x] ; i ; i = e[i].nt) {
        y = e[i].to;
        if (y == fa) continue;
        bl = 1;
        solve (y , x , flg ^ 1);
        if (!flg) res = max (res , ans[y]);
        else res = min (res , ans[y]);
    }
    if (bl) ans[x] = res;
    else ans[x] = f[x];
}
int main () {
    scanf ("%d" , &n);
    fu (i , 1 , n) scanf ("%d" , &a[i]);
    int u , v;
    fu (i , 1 , n - 1) {
        scanf ("%d%d" , &u , &v);
        add (u , v) , add (v , u);
    }
    dfs (1 , 0);
    solve (1 , 0 , 0);
    printf ("%d" , ans[1]);
    return 0;
}