目录

灰色关联度矩阵

关联系数

计算关联系数公式

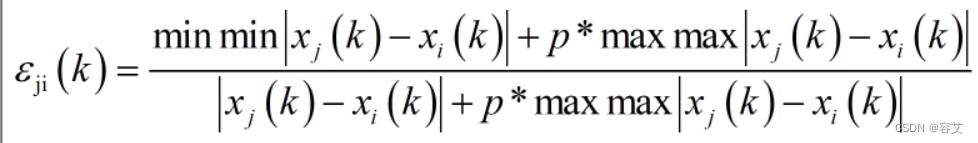
步骤

• 第一步

• 第二步

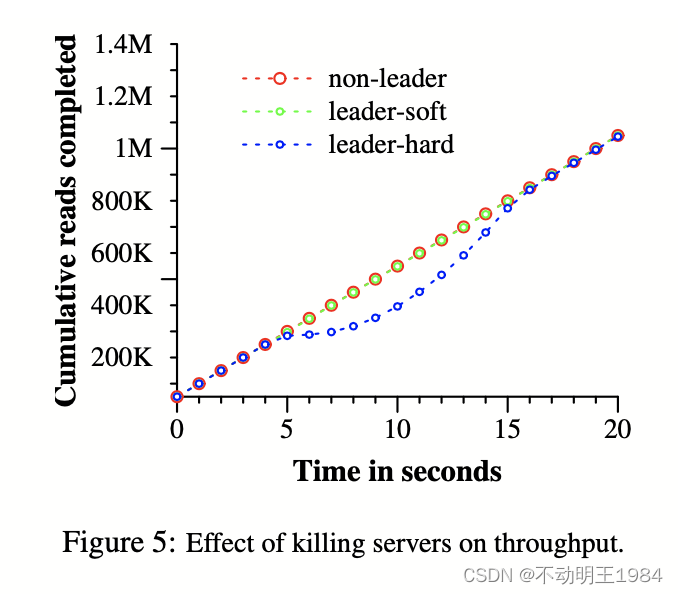
求参考数列和待比较数列矩阵数值做差之后的最小值和最大值

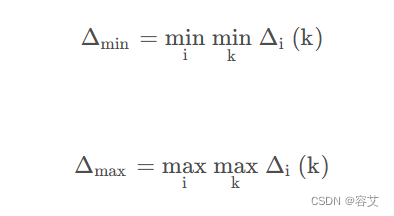
• 第三步利用公式计算关联度系数，其中将最大值最小值耦合到关联系数中，可以保证关联系数位于[0,1]之间，同时上下对称的结构可以消除量纲不同和数值量级悬殊的问题

注意：p一般取0.5

关联矩阵

关联系数只能反映点与点之间的关系，相关性信息分散，因此我们定义相关度r

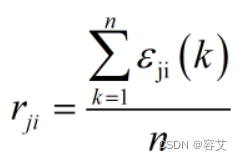
• |r|>0.7称为强相关，|r|<0.3称为弱相关
• 按 r大小排序 ，区分其关联程度的大小，若r值越大，说明其关联的程度越大；反之r值越小，则其关联程度越小

GM(1,1)模型

相关原理

• 第一步：进行累加

• 第二步：求出累加数列的灰导数方程

• 第三步：定义累加数列的紧邻均值
  
• 第四步：定义GM(1,1)灰微分方程，并求出发展系数a和灰作用量b

此处采用z而不用x(1)是因为防止原始数列存在突变的奇异数据

• 第五步：白化模型

即用来代替z，用已知信息代替灰色信息

• 第六步：求出预测方程
• 第七步：模型检验（相对残差，方差比，小误差概率验证）
• 可行性分析：利用级比来判断

matlab程序

clear
syms a b;
c=[a b]';
A=[89677,99215,109655,120333,135823,159878,182321,209407,246619,300670];
B=cumsum(A);  % 原始数据累加
n=length(A);
for i=1:(n-1)
    C(i)=(B(i)+B(i+1))/2;  % 生成邻近均值矩阵
end
%求出a,b
D=A;
D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
%disp(a+" "+b)
%预测以后的数据
F=[];
F(1)=A(1);
for i=2:(n+10)
    F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a;
end

G=[];
G(1)=A(1);
for i=2:(n+10)
    G(i)=F(i)-F(i-1);
end
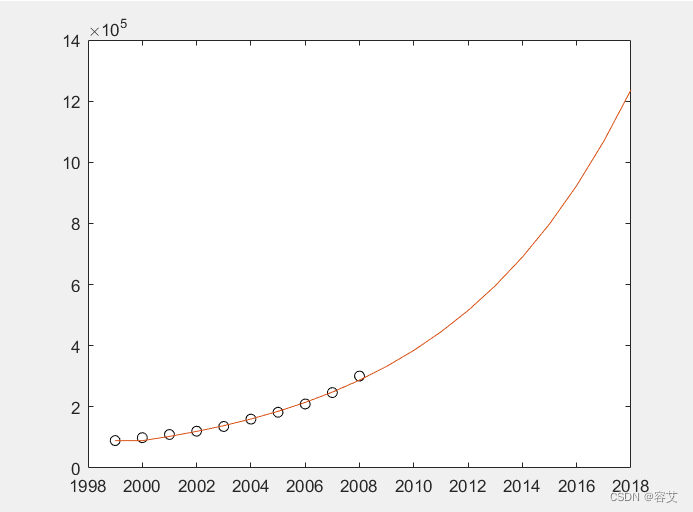
t1=1999:2008;
t2=1999:2018;
plot(t1,A,'ko')
hold on
plot(t2,G)

预测结果图