海明码（汉明码）是一种利用奇偶性检测和纠正错误的编码方法。在传输和储存数据时，可能会发生传输错误或数据损坏。海明码通过在数据中添加冗余位来检测错误并进行纠正，提高了传输和存储数据的可靠性。

基本原理：将原始数据分成若干个数据块，并在每个数据块中增加一定数量的校验位，用于检测错误或进行纠正。在数据传输或存储时，接收方会对收到的数据进行校验，检测出错误后通过校验位进行错误纠正，最终得到正确的原始数据。

优点和缺点：能够在较少的冗余位数量下实现高效的错误检测和纠正。缺点是海明码的容错能力有一定限制，当出现多个位错误时可能无法纠正。

海明码的构成方法是在数据位之间的特定位置上插入k个检验位，通过扩大码距来实现检错和纠错。

设数据位是 n 位，校验位是 k 位，则 n 和 k 必须满足以下关系：

只有当满足以上不等式，海明码才具有检错功能

海明码编码规则如下：

设 k 个校验位为Pk，Pk-1，...，P1，n 个数据位为Dn-1，Dn-2，...，D1，D0，对应的海明码为Hn+k，Hn+k-1，...，H1

第一步： Pi 在海明码的第  位置，即Hj = Pi，且j=，数据位则依序从低到高占据海明码中剩下的位置。

第一步什么意思呢，我们来拿一个8位的数据位来举例，首先根据海明码的构成方式，数据位 n = 8，则代入 ，k = 4，即校验位为 4 位，那么整个海明码的编码位数一共是 12 位。如下图所示：

根据第一步规则，我们选取所有符合要求的 i 值，即 i = 1，2，3，4符合要求，则 Pi 分别在第1，2，4，8个位置，那么我们给出海明码校验位的位置后，依次将数据位从低到高插入剩下的位置。

此时，第一步已经完成，下面开始进行第二步。

第二步：海明码中的任何一位都是由若干个校验位来校验的。其对应关系如下：被校验的海明位的下标等于所有参与校验该位的校验位的下标之和，而校验位由自身校验。 

对于 8 位的数据位，进行海明校验需要 4 个校验位。令数据位为D7，D6，D5，D4，D3，D2，D1，D0，校验位为P4，P3，P2，P1，形成的海明码为H12，H11，…，H3，H2，H1，则编码过程如下。

确定校验关系，如下表所示：

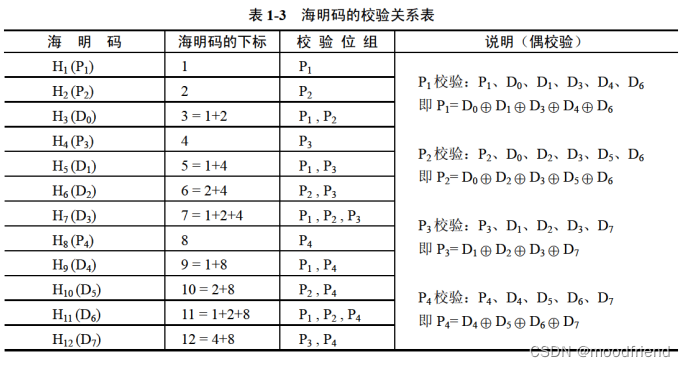
如果采用奇校验，则将各校验位的偶校验值取反即可。

注意：  符号表示异或操作

这个表是书上的一个表，大家可能看起来不太好理解，我总结了一个表：

对于这个表，从 1 到 12 都可以看作是 2 的几次幂的和，那么我们找出包含有相同次幂的组合 

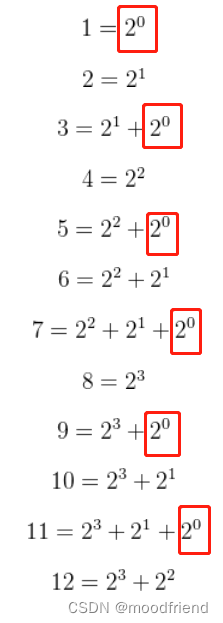
以上六个式子包含有 ，分为一组，对应的海明位分别是1，3，5，7，9，11（P1，D0，D1，D3，D4，D6），对应前面图中的P1校验

以上六个式子包含有 ，分为一组，对应的海明位分别是2，3，6，7，10，11（P2，D0，D1，D3，D5，D6），对应前面图中的P2校验

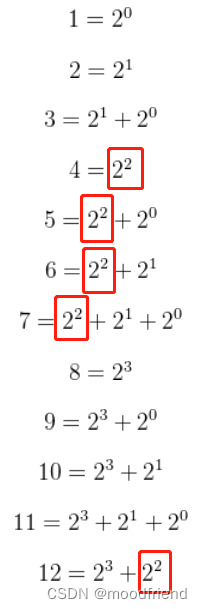
以上六个式子包含有 ，分为一组，对应的海明位分别是4，5，6，7，12（P3，D1，D2，D3，D7），对应前面图中的P3校验

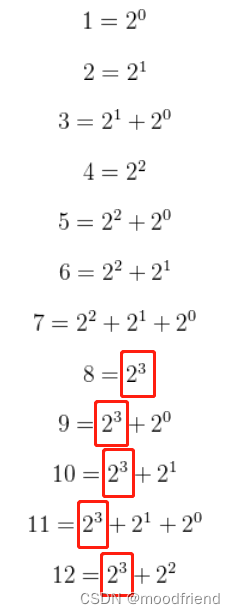
以上六个式子包含有 ，分为一组，对应的海明位分别是8，9，10，11，12（P4，D4，D5，D6，D7），对应前面图中的P4校验

这样经过第二步后，我们就得出了四个校验组。

第三步：检验错误，对使用海明编码的数据进行差错检测。

若采用偶校验，则 G1G2G3G4 全为 0 时表示接收到的数据无错误（奇校验应全为1）。当  G1G2G3G4 不全为 0 时说明发生了错误，G1G2G3G4的十进制值能够指出发生错误的位置，例如G1G2G3G4 = 1001，说明H9（D4）这个位置出现了差错，将其取反即可纠正错误。

再来看一个例题：

以上就是关于海明码的原理及相关计算，如有错误，欢迎指正！