对于Ax=b,我们要迅速想到线性组合,如下,
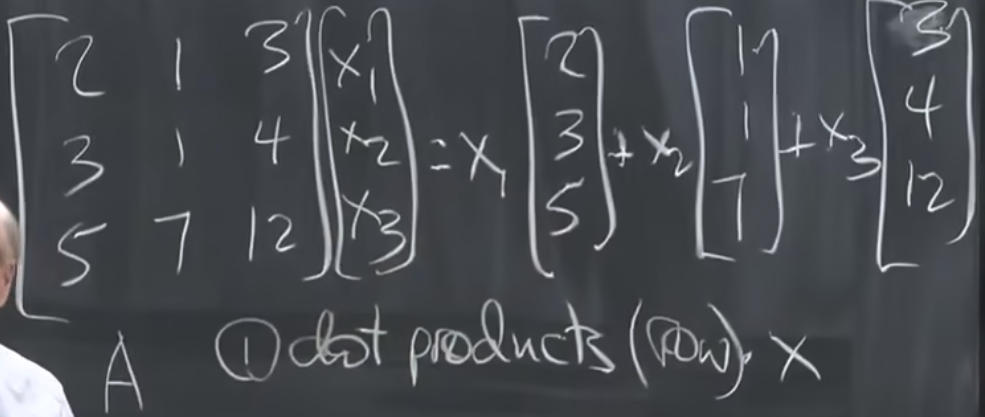
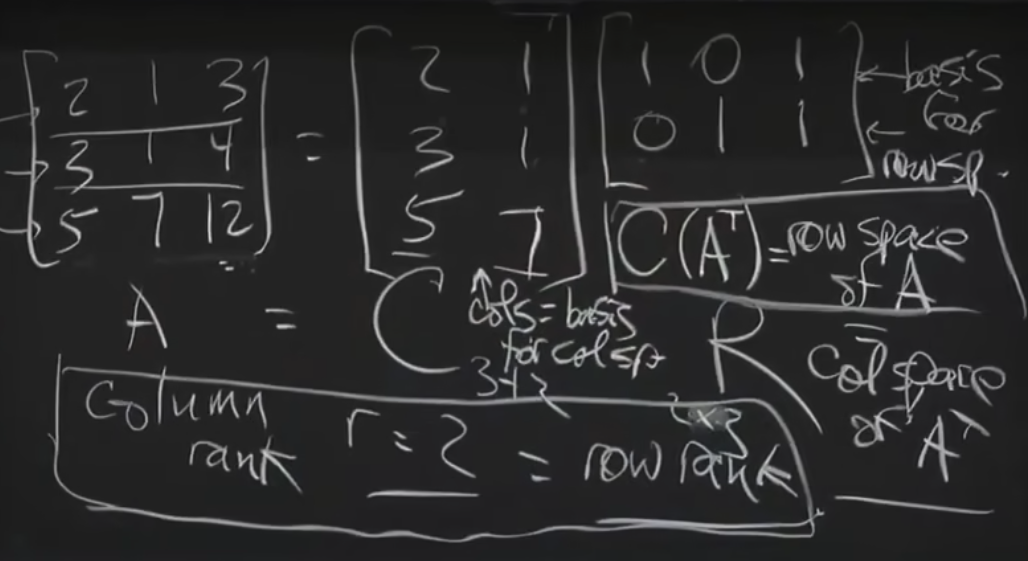
我们也可以使用rank秩来反应一个矩阵的特征,如果满秩则可以表示整个向量空间,如上只有两个independent column,它的rank==2,表达一个plane平面。
接下来我们将引入矩阵中的因式分解A=CR的例子,如下,我们能够将秩为2的矩阵分解为两个秩为2的矩阵相乘。
接下来我们将介绍一下两个mxn和nxp的矩阵要进行多少次乘法运算,当然是mxnxp次乘法运算。
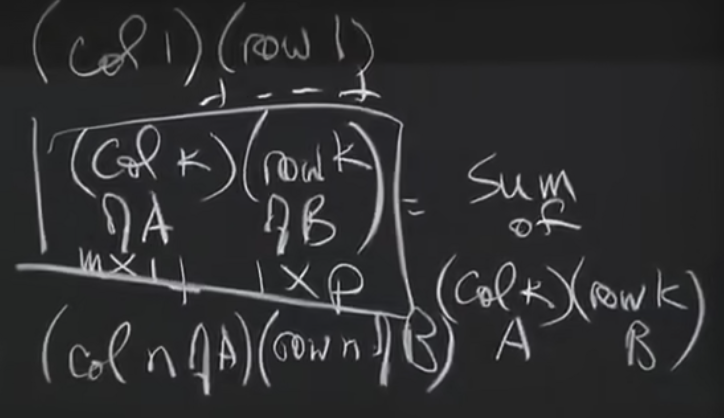
对于Ax=b,我们要迅速想到线性组合,如下,
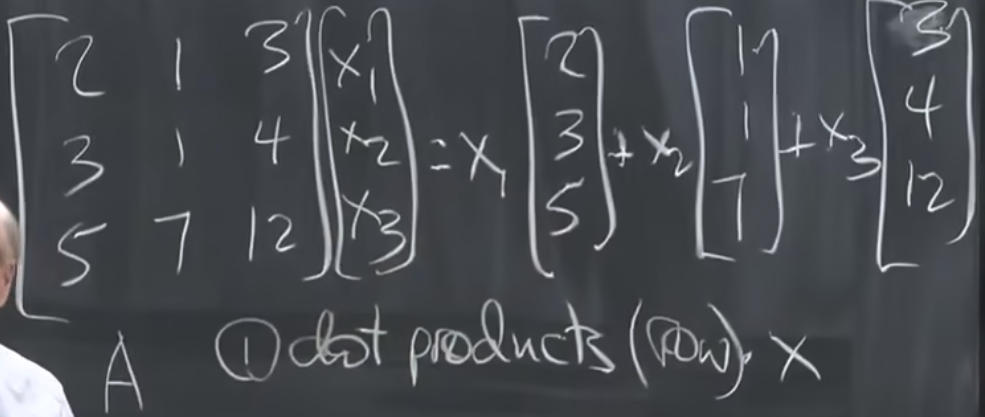
我们也可以使用rank秩来反应一个矩阵的特征,如果满秩则可以表示整个向量空间,如上只有两个independent column,它的rank==2,表达一个plane平面。
接下来我们将引入矩阵中的因式分解A=CR的例子,如下,我们能够将秩为2的矩阵分解为两个秩为2的矩阵相乘。

接下来我们将介绍一下两个mxn和nxp的矩阵要进行多少次乘法运算,当然是mxnxp次乘法运算。
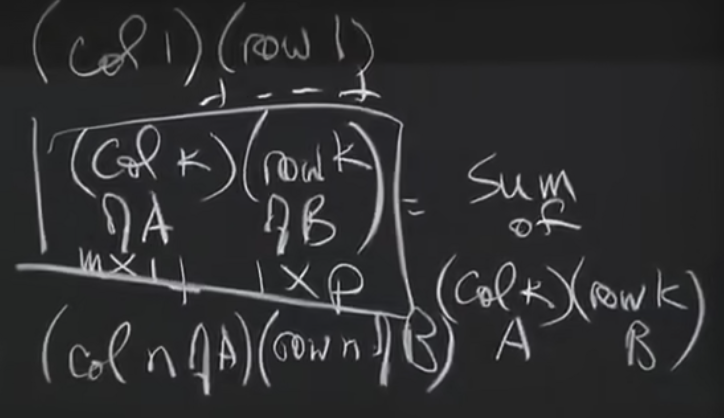
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/730929.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!