昨天,我们分享过一篇文章《串行组合模型及信用评估场景实践》,里边详细介绍了串行组合模型的原理逻辑,以及在信用风险评估场景的具体实现过程。同时,从模型串联数量、排列顺序等多个维度验证了串行组合模型的合理性与有效性,不仅体现在串联模型相比单一模型的效果更佳外,而且还说明模型串行顺序有利于综合模型性能的调优,从而有效证明了串行组合模型在实际建模场景的价值。
作为组合模型内容的姊妹篇,本文将为大家介绍下并行组合模型的实现过程,以及在实际业务场景中的应用效果。
1、并行组合模型原理
并行组合模型与串行组合模型同理,也是多个单一模型的叠加融合结果,主要区别在于各个子模型的流转过程是以并列的方式呈现,具体示意图如图1所示。其中,模型1/2/3的输入数据均为原始样本,输出数据为各模型的预测结果,最终总模型是将各个子模型的输出数据以投票(分类)或代数(回归)的方式进行汇总融合,这种方式也是并行组合模型的最大优点,可以将各个单一模型的误差得以平衡,不会因某个模型的误差较大而过度影响最终的决策效果。
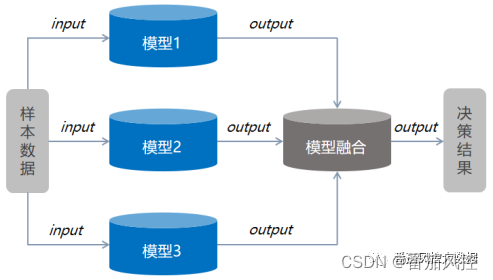
图1 并行组合模型示意图
对于模型融合环节,当模型为分类问题时,例如模型预测结果为二分类(0/1)或多分类(0/1/2),则综合模型最终结果的生成通常采用投票法,具体包括简单投票、加权投票等;当模型为回归问题时,例如模型预测结果为0至1000范围的连续数值,则综合模型最终结果的生成通常采用代数法,具体包括直接平均、加权求和等。多个模型融合的输出数据(投票或平均),便是综合模型的决策分析结果。
并行组合模型与串行组合模型类似,根据模型算法的类型不同,可以分为同类并行组合模型、异类并行组合模型。同时,异类组合形式在实际业务中应用场景较多,以回归机器学习算法为例,常采用的模型包括线性回归、支持向量机回归、K近邻回归、决策树回归、XGBoost回归、随机森林回归等。下面我们将围绕信贷风控典型的额度定价授信场景,结合具体的实例样本数据,来构建一个异类并行组合模型。
2、实例样本数据描述
针对异类并行组合模型的算法类型不同,本文选取线性回归、XGBoost、决策树、K近邻、随机森林共5个算法来实现模型融合。同时,由于本场景的额度定价为回归问题,因此以上各机器学习模型均采用回归算法。本实例的样本数据包含10000条样本与9个字段,部分数据样例如图2所示。其中,id为样本主键,credit_apply、call_total等7个特征为X变量池,credit_amount为目标变量Y,具体特征字典如图3所示。
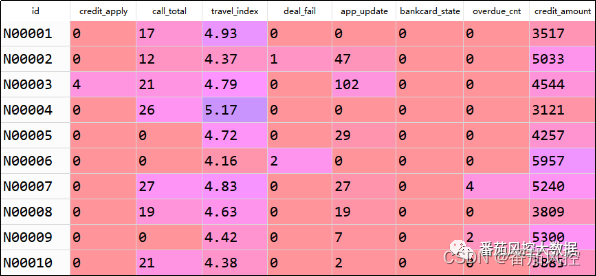
图2 样本数据样例
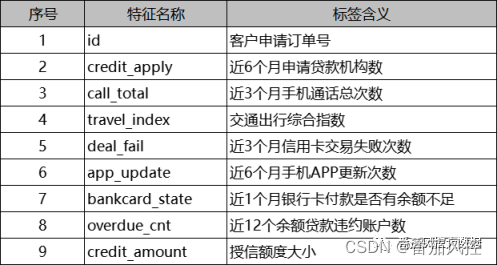
图3 样本特征字典
根据以上样本数据,现构建一个贷前额度定价授信模型,即通过credit_apply、call_total、travel_index等7个特征变量对目标变量credit_amount进行拟合训练。其中,特征变量的简单描述性统计分布eda结果如图4所示。为了便于了解目标变量credit_amount取值分布情况,我们通过图5的代码实现过程,来完成目标变量的直方图输出,具体可视化分布结果如图6所示。
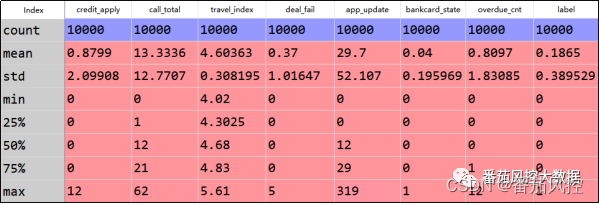
图4 特征变量eda分布
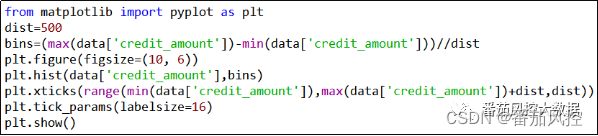
图5 目标变量可视化实现
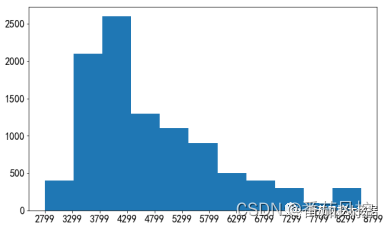
图6 目标变量直方图分布
3、特征变量性能分析
为了有效避免模型训练后出现较强的模型共线性现象,在模型变量拟合之前,有必要对各特征变量进行简单的特征工程分析,例如特征相关性、特征共线性等,这里分别采用pearson系数与VIF系数来进行评价,具体分布结果如图7、8所示(实现过程详见本文代码附件)。
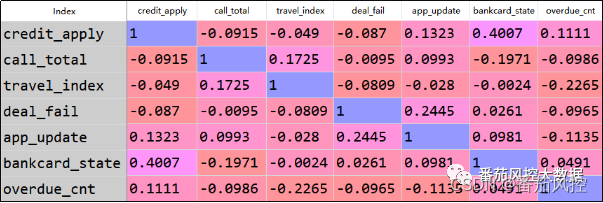
图7 特征pearson系数

图8 特征VIF系数
由以上结果可知,特征变量之间的相关性系数整体表现偏低,最大系数值不超过常见阈值0.5,说明特征之间的相关性表现较弱;特征VIF系数值最大值仅有2.96617,远低于业务中的判断阈值10。因此,本样本数据的特征字段相互没有较强的相关性,有利于后续模型训练环节的变量拟合。
4、单一模型拟合训练
本文实现的异类模型并行组合,采用的机器学习回归算法分别为线性回归LinR、XGBoost、决策树Tree、K近邻KNN、随机森林RF共5个类型。对于最终并行模型的融合,输入数据为各子模型的预测结果,因此我们需要依次训练拟合各个子模型,并将输出数据分别保存,以作为综合模型的策略数据输入。此外,为了评估综合并行模型的性能优势,我们有必要对各个子模型进行效果评估,这里采用回归模型常见评价指标R2来量化分析。
对于模型构建环节,我们从整体的建模样本数据抽取70%来训练模型,其余30%数据用来测试模型,最后我们分别输出训练集train与测试集test的模型R2指标,除了量化分析模型整体表现之外,重点来对比描述各模型应用的稳定度情况。各个子回归算法模型(LinR、XGB、Tree、KNN、RF)的模型训练与模型评估过程,具体实现分别如图9~13所示。
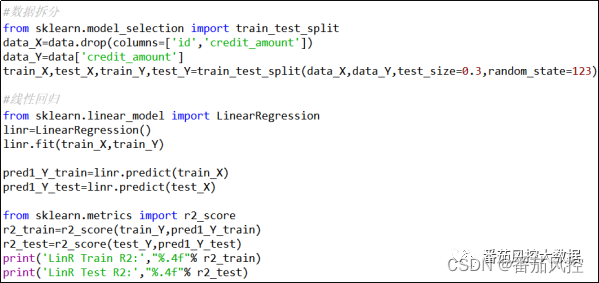
图9 线性回归LinR模型
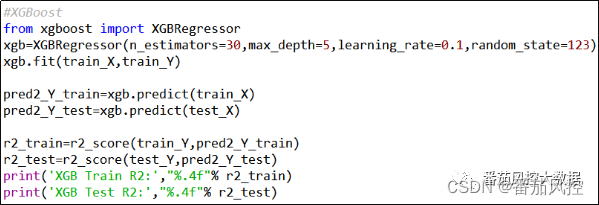
图10 XGBoost回归模型
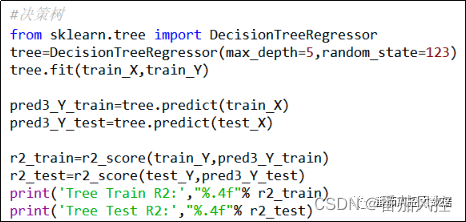
图11 决策树Tree回归模型
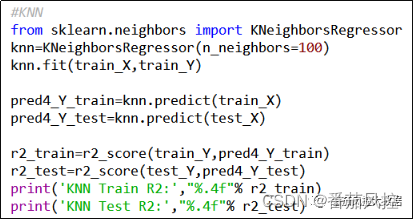
图12 K近邻KNN回归模型

图13 随机森林RF回归模型
通过以上各子模型的训练与预测,训练集train与测试集test的模型性能指标R2表现具体如图14所示。根据模型拟合优度R2指标评价方法(取值范围0~1,取值越大模型效果越好),可见各模型在训练样本与测试样本的性能表现均较好。
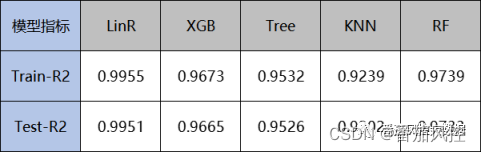
图14 子模型R2评价指标
5、并行组合模型实现
当各个子模型完成拟合训练后,我们将训练集与测试集的预测结果数据分别进行保存(pred1_Y_trainpred5_Y_train、pred1_Y_testpred5_Y_test),作为并行组合模型的输入数据。对于模型的并行融合,由于本例的额度定价为回归场景,因此可采用简单平均或加权平均的方法来实现,这里通过简单的直接平均来完成,即将各模型的预测结果pred1_Y_train~pred5_Y_train求和,然后再除以子模型数量5,从而得到训练数据的模型并行结果pred_mean_train,测试数据的模型并行与此同理。模型在训练集与测试集的模型并行组合,具体实现过程如图15所示。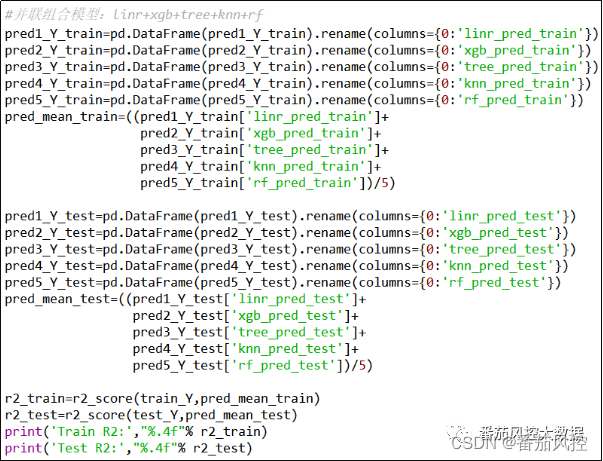
图15 模型并行组合实现
模型并行组合后,同样输出综合模型在训练样本与测试样本的评价指标R2,这里将各子模型的性能表现进行汇总分析,具体结果如图16所示。模型并行组合模型的主要优势并非某个维度的性能指标表现很好,而是经过融合的组合模型在应用过程中较为稳定。从表中结果可以看出,对于各子模型与综合模型的整体效果均表现较好,在这种情形下,我们需要重点评估下模型的稳定度情况。因此,这里引入误差指标的量化分析,具体逻辑是指模型在测试集test的R2表现,相对训练集train指标的差异程度。以子模型LinR为例,误差error=abs(1-(0.9951/0.9955))=0.000402,对于其他模型,按照此方法同理实现。从分布结果来看,并行组合模型的误差0.000203相对其他各子模型表现最小,说明综合并行组合模型在训练样本与测试样本的稳定性最好,这也是并行组合模型的优势,可以平衡各子模型的预测误差,从而有效保证模型应用的稳定程度。
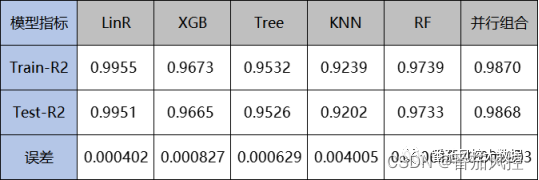
图16 并行模型性能分析
综合以上内容,我们围绕模型并行组合的原理思想,通过信贷额度定价的具体实例场景,实现了并行组合模型的完整建立过程,并通过模型指标验证了并行组合模型的稳定性能优势,从而为实际建模场景的模型优化提供价值参考。为了便于大家对并行组合模型的进一步理解与熟悉,本文额外附带了与以上内容同步且更详细的代码与数据,供大家参考学习,详情请移至知识星球查看相关内容。
…
~原创文章