【图像处理OpenCV(C++版)】——2.2 OpenCV之矩阵运算详解(全)

news2024/11/17 9:57:24

前言：

😊😊😊欢迎来到本博客😊😊😊

🌟🌟🌟 本专栏主要结合OpenCV和C++来实现一些基本的图像处理算法并详细解释各参数含义，适用于平时学习、工作快速查询等，随时更新。

😊😊😊 具体食用方式：可以点击本专栏【OpenCV快速查找(更新中)】–>搜索你要查询的算子名称或相关知识点，或者通过这篇博客👉通俗易懂OpenCV(C++版)详细教程——OpenCV函数快速查找(不断更新中)]查阅你想知道的知识，即可食用。

🎁🎁🎁支持：如果觉得博主的文章还不错或者您用得到的话，可以悄悄关注一下博主哈，如果三连收藏支持就更好啦！这就是给予我最大的支持！😙😙😙

文章目录

    • 学习目标
    • 一、 常见矩阵运算
      • 1.1 加法运算
      • 1.2 减法运算
      • 1.3 点乘运算
      • 1.4 点除运算
      • 1.5 乘法运算
    • 二、 其他运算
      • 2.1 指数和对数运算
      • 2.2 幂指数和开平方运算
      • 2.3 矩阵运算函数表(全)
    • 三、 总结

学习目标

  • 学会加法运算
  • 学会减法运算
  • 学会点乘运算
  • 学会点除运算
  • 学会乘法运算
  • 其他运算介绍

一、 常见矩阵运算

  矩阵运算在学习其他课程(矩阵论、线性代数、高数)多少都有涉及。在数字图像处理中，可以理解为图像即多维矩阵，在图像处理中一般用到的关于矩阵的运算包括：加法、减法、点乘、点除、乘法等，下面我们一一介绍每个运算算子用法及注意点。

1.1 加法运算

  矩阵加法：两个矩阵对应位置的数值相加。例如：

  第一种方式：很简单，就如同数学加法。使用OpenCV重载的“+”运算符：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int  main(int argc, char**argv) {

	/*1.1 加法运算*/
	Mat m1 = (Mat_<uchar>(3, 2) << 11, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<uchar>(3, 2) << 12, 11, 22, 21, 32, 31);

	Mat dst = m1 + m2;
	cout << "加法运算结果为：" << dst << endl;

	return 0;
}

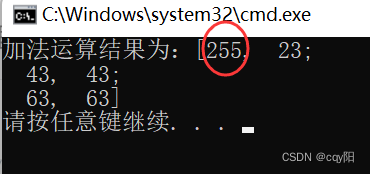
  我们可以看到200+150应该等于350，得到得结果却是255。原因是两个矩阵的数据类型都是uchar，所以用“+”运算符计算出来的和也是uchar类型的，但是uchar类型范围的最大值是255，所以只好将350截断为255。
  但是，利用“+”运算符计算Mat的和还有一点需要特别注意：两个Mat的数据类型必须是一样的，否则会报错，也就是用“+”求和是比较严格的。

  同时，一个数值与一个Mat对象相加，也可以使用“+”运算符，但是无论这个数值是什么数据类型，返回的Mat的数据类型都与输入的Mat相同。比如一个数值与上面的uchar类型的m2相加，代码如下：

#include <iostream>
#include <opencv2/opencv.hpp>

using namespace std;
using namespace cv;

int  main(int argc, char**argv) {


	/*1.1 加法运算*/
	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<uchar>(3, 2) << 150, 11, 22, 21, 32, 31);

	Mat dst = m1 + m2;
	cout << "加法运算结果为：" << dst << endl;


	float value = 50;
	Mat dst1 = value + m2;
	cout << "50+矩阵m2结果为：" << dst1 << endl;

	return 0;
}

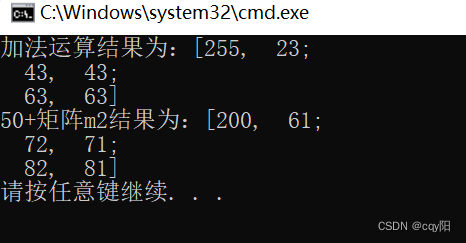
注意：如果value是float类型的，但是因为m2是uchar类型的，所以返回的dst1也是uchar类型的，结果超过255都会截断为255。

  
  第二种方式：上面介绍中可以看出，第一种方式有一定得局限性，所以我们可以利用OpenCV得函数add()，结构如下：

void add(InputArray srcl, InputArray src2, OutputArray dst, InputArray mask=noArray(), int dtype=-1)

  案例如下：

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;

int  main(int argc, char**argv) {
	/*  函数add*/
	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<float>(3, 2) << 150, 11, 22, 21, 32, 31);
	Mat dst;
	
	add(m1, m2, dst, Mat(), CV_64FC1);
	cout << "加法运算add()结果为：" << dst << endl;
	
	return 0;
}

  案例中以看出，add()函数输入矩阵的数据类型可以不同，而输出矩阵的数据类型可以根据情况自行指定。
  需要特别注意的是：如果给dtype赋值为-1，则表示dst的数据类型和src1、src2是相同的，也就是只有当src1和src2的数据类型相同时，才有可能令dtype=-1，否则会报错。

  
  两个向量也可以做加法运算，比如：

	Vec3f v1 = Vec3f(1, 2, 3);
	Vec3f v2 = Vec3f(4,5,6);
	Vec3f dstV = v1 + v2;
	cout << dstV;

结果：

[5，7，9]

  

1.2 减法运算

  矩阵的减法与加法类似，但是也有几点注意点。
  第一种方式：也很简单，就如同数学减法。使用OpenCV重载的“-”运算符：

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;

int  main(int argc, char**argv) {
	/*1.2 减法运算*/

	/*   运算符 - */
	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<uchar>(3, 2) << 150, 11, 22, 21, 32, 31);

	Mat dst = m1 - m2;
	cout << "减法运算结果为：" << dst << endl;

	return 0;
}

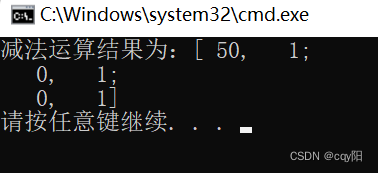
  同样我们可以看到12-11应该等于-1，以此类推，得到得结果却是0。原因也是两个矩阵的数据类型都是uchar，所以用“-”运算符计算出来的和也是uchar类型的，但是uchar类型范围的最小值是0，所以只好将负数截断为0。

  
  第二种方式：和加法一样，Mat对象与一个数值相减，也可以使用“-”运算符。当然，也存在与“+”运算符一样的不足。所以OpenCV提供了subtract()函数，结构如下：

void subtract(InputArray srcl, InputArray src2, OutputArray dst, InputArray mask=noArray(), int dtype=-1)

  可以实现不同的数据类型的Mat之间做减法运算，与add()函数类似，这里不作详细叙述，可以利用上面代码进行修改即可。

  

1.3 点乘运算

  矩阵的点乘即两个矩阵对应位置的数值相乘。
  对于两个矩阵的点乘，可以利用Mat的成员函数mul()，两个Mat对象的数据类型必须相同才可以进行点乘，返回的矩阵的数据类型不变。我们依旧以m1和m2矩阵为例：

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;

int  main(int argc, char**argv) {
	/*1.3 点乘运算*/
	
	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<uchar>(3, 2) << 150, 11, 22, 21, 32, 31);
	Mat dst = m1.mul(m2);
	cout << "点乘运算结果为：" << dst << endl;
	
	return 0;
}

  结果可以看出，点乘后对大于255的数值做了截断处理。为了不损失精度，可以将两个矩阵设置为int、float等数值范围更大的数据类型。

  
  OpenCV提供了multiply()函数：

void multiply(InputArray srcl, InputArray src2, OutputArray dst, double scale=1, int dtype=-1)

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/*点乘运算multiply() */

	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<float>(3, 2) << 150, 11, 22, 21, 32, 31);

	Mat dst;
	multiply(m1,m2,dst,1.0, CV_64FC1);
	cout << "multiply()点乘运算结果为：" << dst << endl;

	return 0;
}

  multiply()函数使用起来更加灵活，矩阵m1和m2的数据类型不一定需要相同，可以通过参数dtype指定输出矩阵的数据类型。
  注意：第四个参数：scale(dst=sclae*m1*m2)，即在点乘结果的基础上还可以再乘以系数scale。

  

1.4 点除运算

  点除运算与点乘运算类似，是两个矩阵对应位置的数值相除。

  第一种方式：与“+”和“-”类似，可以使用“/”运算符，两个Mat的数据类型相同且返回的Mat也是该数据类型。

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/*点除运算  / */

	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<uchar>(3, 2) << 150, 11, 22, 21, 32, 31);


	Mat dst = m1 / m2;
	cout << "/点除运算结果为：" << dst << endl;


	return 0;
}

  需要注意：如果分母为0的除法运算时，默认得到的值为0。
  同样，用一个数值与Mat对象相除也可以使用“/”运算符，且返回的Mat的数据类型与输入的Mat的数据类型相同，与输入数值的数据类型是没有关系的。

  
  第二种方式：使用“/”运算符和上面一样会存在一定局限性，OpenCV提供了divide()函数:

void divide(InputArray srcl, InputArray src2, OutputArray dst, double scale=1, int dtype=-1)

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/*点除运算 divide() */

	Mat m1 = (Mat_<uchar>(3, 2) << 200, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<float>(3, 2) << 150, 11, 22, 21, 32, 31);

	Mat dst;
	divide(m1, m2, dst, 1.0, CV_64FC1);
	cout << "divide()点除运算结果为：" << dst << endl;

	return 0;
}

  同样注意：第四个参数：scale(dst=sclae*m1/m2)，即在点除结果的基础上还可以再乘以系数scale。

  

1.5 乘法运算

  对于两个矩阵的乘法(矩阵乘法相关知识，线性代数等相关课程详细讲解了，有需要可以自行查阅相关资料，了解矩阵乘法运算规则)，不同于上面得点乘运算。例如：

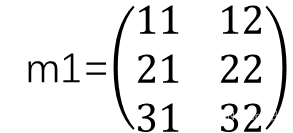
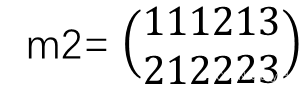
  使用'*'运算符对两个矩阵进行乘法运算：

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 乘法运算*  */

	Mat m1 = (Mat_<float>(3, 2) << 11, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<float>(2, 3) << 11, 12, 13, 21, 22, 23);


	Mat dst = m1 * m2;
	cout << "*乘法运算结果为：" << dst << endl;

	return 0;
}

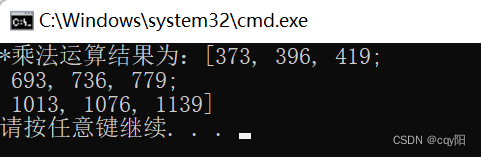
  对于Mat对象的乘法，需要注意两个Mat只能同时是float或者double类型，对于其他数据类型的矩阵做乘法会报错。

  上面介绍了两个float或者double类型的单通道矩阵的乘法。例如：

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 双通道乘法运算*/
	Mat s1 = (Mat_<Vec2f>(2, 1) << Vec2f(1, 2), Vec2f(3, 4));
	Mat s2 = (Mat_<Vec2f>(1, 2) << Vec2f(5,6), Vec2f(7, 8));

	Mat dst1 = s1 * s2;
	
	cout << "双通道*乘法运算结果为：" << endl;
	for (int i = 0; i < dst1.rows; i++)
	{
		for (int j = 0; j < dst1.cols; j++)
		{
			cout << dst1.at<Vec2f>(i, j) << " ";
		}
		cout << endl;
	}
	//cout << "双通道*乘法运算结果为：" << dst1 << endl;

	return 0;
}

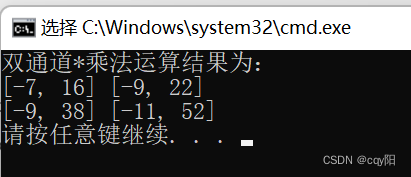
  奇怪的是：怎么会有负数，两个双通道矩阵也可相乘吗？
  实际上，其实这里是将s1和s2这两个双通道Mat对象当作了两个复数矩阵。第一通道存放的是所有值的实部，第二通道存放的是对应的每一个虚部。例如，Vec2f(1，2)可以看作1+2i。

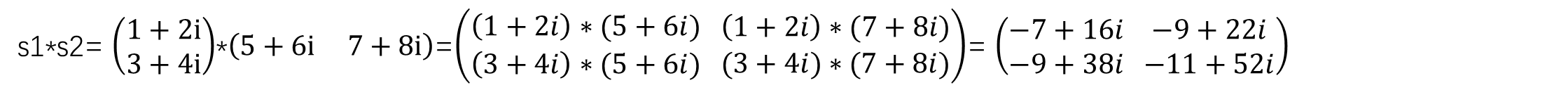
  结果可以很明显地看出，将Vec2f看作了一个复数，例如输出的[-7，16]分别代表复数-7+16i的实部和虚部。

  
  关于矩阵乘法运算，OpenCV也提供了gemm()函数来实现。

void gemm(InputArray src1, InputArray src2, double alpha, InputArray src3, double beta, OutputArray dst, int flags=0 )

  src1：输入类型是CV_ 32F或者CV_64F的单或双通道矩阵；
  src2：输入矩阵，类型与src1一致；
  alpha：src1与src2相乘后得系数；
  src3：输入矩阵，类型与src1一致；
  beta：src3的系数；
  dst：输出矩阵；
  flags：标识符； 0：没有转置；GEMM_1_T：表示src1转置；GEMM_2_T：表示src2转置；GEMM_3_T：表示src3转置；即：

    flags可以组合使用，比如需要src2和src3都进行转置，则令flags=GEMM_2_T+GEMM_3_T。
    当输入矩阵src1、src2、src3是双通道矩阵时，代表是复数矩阵，其中第一通道存储实部，第二通道存储虚部。

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 乘法运算gemm() */
	Mat m1 = (Mat_<float>(3, 2) << 11, 12, 21, 22, 31, 32);
	Mat m2 = (Mat_<float>(2, 3) << 11, 12, 13, 21, 22, 23);
	Mat dst ;
	gemm(m1, m2, 1.0, NULL, 0, dst, 0);
	cout << "gemm乘法运算结果为：" << dst << endl;

	return 0;
}

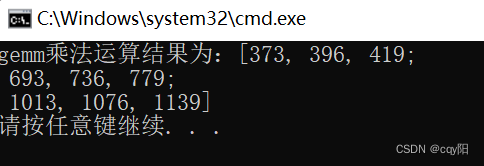
  结果与'*'是等价的。需要注意的是：gemm()也只能接受CV_32FC1、CV_64FC1、CV_32FC2、CV_64FC2数据类型的Mat，这一点与使用'*'也是一样的。

二、 其他运算

2.1 指数和对数运算

  我们讨论的对数和指数运算是对矩阵中的每一个数值进行相应的运算。除此之外，我们也可以使用for循环对矩阵中的每一个数值进行相应的运算。
  针对指数和对数运算，OpenCV分别提供了exp()和log()函数(这里log是以e为底的)。
  需要注意的是：这两个函数的输入矩阵的数据类型只能是CV_32F或者CV_64F，否则会报错。

  (1) 指数运算

  指数运算函数exp()表示： e x e^x ex

exp(InputArray src1,OutputArray dst)

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 指数运算exp() */
	Mat m1 = (Mat_<float>(3, 2) << 11, 12, 21, 22, 31, 32);
	Mat dst;
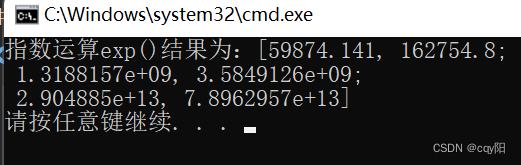
	exp(m1, dst);
	cout << "指数运算exp()结果为：" << dst << endl;

	return 0;
}

  
  (2) 对数运算

  对数运算函数log()表示： log ⁡ e x \log_ex loge​x= ln ⁡ x \ln x lnx

log(InputArray src1,OutputArray dst)

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 对数运算log() */
	Mat m1 = (Mat_<float>(3, 2) << 11, 12, 21, 22, 31, 32);
	
	Mat dst;
	log(m1, dst);
	cout << "对数运算log()结果为：" << dst << endl;
	

	return 0;
}

  注意：除了有log()运算(以e为底)，也有以10、2为底等等对数函数。

2.2 幂指数和开平方运算

  同样，我们讨论的幂指数和开平方运算是对矩阵中的每一个数值进行相应的运算。也是可以使用for循环对矩阵中的每一个数值进行相应的运算，
  针对幂指数和开平方运算，OpenCV分别提供了pow()和sqrt()函数 。

  同样，需要注意的是：sqrt()的输入矩阵的数据类型只能是CV_32F或者CV_64F，而pow()的输入矩阵的数据类型不受限制，且输出矩阵与输入矩阵的数据类型相同。

  
  (1) 幂指数运算

  对数运算函数pow()表示： x n x^n xn，以2次方为例：

pow(InputArray src1,scale,OutputArray dst)

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 幂指数运算pow()*/
	Mat m1 = (Mat_<float>(3, 2) << 11, 12, 21, 22, 31, 32);
	Mat dst;
	pow(m1,2,dst);

	cout << "幂指数运算pow()结果为：" << dst << endl;

	return 0;
}

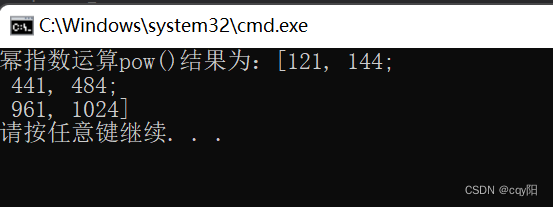
  如果数据类型为Mat m1 = (Mat_<uchar>(3, 2) << 11, 12, 21, 22, 31, 32);，经过幂指数运算的dst的数据类型仍然是uchar，大于255的数值也会截断为255。

  
  (2) 开平方运算

  开平方运算函数sqrt()表示： x \sqrt x x ​

sqrt(InputArray src1,OutputArray dst)

#include <iostream>
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int  main(int argc, char**argv) {
	/* 开平方运算sqrt()*/

	Mat m1 = (Mat_<float>(3, 2) << 11, 12, 21, 22, 31, 32);
	Mat dst;
	sqrt(m1, dst);

	cout << "开平方运算sqrt()结果为：" << dst << endl;

	return 0;
}

  

2.3 矩阵运算函数表(全)

  关于矩阵的运算先了解这些最基本的函数即可，OpenCV还提供了很多矩阵运算函数，如取绝对值、求逆、取最大值函数，后面博客中会用到这些函数，到时我们再详细讨论，这边给出其他矩阵运算函数表(供参考，部分函数详细内容可查阅相关资料，或关注本专栏后面博客)：

函数名注释备注
add()矩阵加法详见本章内容
scaleAdd()矩阵加法，带有缩放因子dst(I) = scale * src1(I) + src2(I)
subtract()矩阵减法详见本章内容
multiply()矩阵点乘矩阵逐元素乘法，同mul()函数，与A*B区别
gemm()广义的矩阵乘法操作详见本章内容
divide()矩阵逐元素除法，与A/B区别详见本章内容
abs()对每个元素求绝对值abs(InputArray src)
absdiff()两个矩阵的差的绝对值absdiff(InputArray src1,InputArray src2,OutputArray dst)
exp()指数运算详见本章内容
pow()幂运算详见本章内容
log()对数运算详见本章内容
sqrt()开平方运算详见本章内容
min, max()每个元素的最小值或最大值返回这个矩阵 dst(I) = min(src1(I), src2(I)), max同min(InputArray src1,InputArray src2)
minMaxLoc()定位矩阵中最小值、最大值的位置minMaxLoc( const Mat& src, double* minVal, double* maxVal=0, Point* minLoc=0, Point* maxLoc=0, const Mat& mask=Mat() );
compare()返回逐个元素比较结果的矩阵——
bitwise_and, bitwise_not, bitwise_or, bitwise_xor每个元素进行位运算，分别是和、非、或、异或, max同——
randu以Uniform分布产生随机数填充矩阵同 RNG::fill(mat, RNG::UNIFORM))
randn以Normal分布产生随机数填充矩阵同 RNG::fill(mat, RNG::NORMAL))
theRNG()随机打乱一个一维向量的元素顺序返回一个默认构造的RNG类的对象theRNG()::fill(…)——
reduce()矩阵缩成向量——
repeat()矩阵拷贝的时候指定按x/y方向重复——
split()多通道矩阵分解成多个单通道矩阵见上一章
merge()多个单通道矩阵合成一个多通道矩阵见上一章
mixChannels()矩阵间通道拷贝如Rgba[]到Rgb[]和Alpha[]
sort, sortIdx()为矩阵的每行或每列元素排序——
setIdentity()设置单元矩阵——
completeSymm()矩阵上下三角拷贝——
inRange()检查元素的取值范围是否在另两个矩阵的元素取值之间，返回验证矩阵——
sum()求矩阵的元素和——
mean()求均值——
meanStdDev()均值和标准差——
countNonZero()统计非零值个数——
cartToPolar, polarToCart()笛卡尔坐标与极坐标之间的转换——
flip()矩阵翻转——
transpose()矩阵转置——
trace()矩阵的迹——
determinant()行列式det(A)
eigen()矩阵的特征值和特征向量——
invert()矩阵的逆或者伪逆比较 Mat::inv()
magnitude()向量长度计算dst(I) = sqrt(x(I)2 + y(I)2)
Mahalanobis()Mahalanobis距离计算——
phase()相位计算，即两个向量之间的夹角——
norm()求范数，1-范数、2-范数、无穷范数——
normalize()标准化——
mulTransposed()矩阵和它自己的转置相乘 AT * Adst = scale(src - delta)T(src - delta)
convertScaleAbs()先缩放元素再取绝对值，最后转换格式为8bit型——
calcCovarMatrix()计算协方差阵——
solve()求解1个或多个线性系统或者求解最小平方问题(least-squares problem)——
solveCubic()求解三次方程的根——
solvePoly()求解多项式的实根和重根——
dct, idct()正、逆离散余弦变换idct同dct(src, dst, flags
dft, idft()正、逆离散傅立叶变换idft同dft(src, dst, flags
LUT()查表变换——
getOptimalDFTSize()返回一个优化过的DFT大小——
mulSpecturms()两个傅立叶频谱间逐元素的乘法——

三、 总结

  最后，长话短说，大家看完就好好动手实践一下，切记不能三分钟热度、三天打鱼，两天晒网。OpenCV是学习图像处理理论知识比较好的一个途径，大家也可以自己尝试写写博客，来记录大家平时学习的进度，可以和网上众多学者一起交流、探讨，有什么问题希望大家可以积极评论交流，我也会及时更新，来督促自己学习进度。希望大家觉得不错的可以点赞、关注、收藏。

🚶🚶🚶今天的文章就到这里啦~
喜欢的话，点赞👍、收藏⭐️、关注💟哦 ~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/73053.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

一篇文章让你认识与学习bash（干货满满）

一篇文章让你认识与学习bash（干货满满）

Linux界存在着这样一种说法&#xff1a;“在Linux的环境下&#xff0c;如果你不懂bash是什么&#xff0c;那么其他的东西就不用学了。”bash的学习是所有命令行模式与未来主机维护与管理的重要基础&#xff0c;所以得认真对待。 一.硬件、内核与shell 1.1 什么是shell? 看下图…
阅读更多...
Linux下安装mysql5.7.18

Linux下安装mysql5.7.18

查询mysql的安装文件&#xff1a; find / -name mysql有安装mysql的路径&#xff0c;有是存放MySQL安装包的路径 卸载mysql: 删除安装路劲 rm -rf /opt/mysql删除配置文件 rm -rf /etc/my.cnf删除/etc/init.d/下跟mysql有关的全部文件&#xff0c;一般包括mysql文件或mys…
阅读更多...
浅尝Go语言的协程实现

浅尝Go语言的协程实现

文章目录为什么需要协程协程的本质协程如何在线程中执行GMP调度模型协程并发为什么需要协程 协程的本质是将一段数据的运行状态进行打包&#xff0c;可以在线程之间调度&#xff0c;所以协程就是在单线程的环境下实现的应用程序级别的并发&#xff0c;就是把本来由操作系统控制…
阅读更多...
微服务框架 SpringCloud微服务架构 25 黑马旅游案例 25.1 搜索、分页

微服务框架 SpringCloud微服务架构 25 黑马旅游案例 25.1 搜索、分页

微服务框架 【SpringCloudRabbitMQDockerRedis搜索分布式&#xff0c;系统详解springcloud微服务技术栈课程|黑马程序员Java微服务】 SpringCloud微服务架构 文章目录微服务框架SpringCloud微服务架构25 黑马旅游案例25.1 搜索、分页25.1.1 直接开干25 黑马旅游案例 25.1 搜…
阅读更多...
PyTorch~自定义数据读取

PyTorch~自定义数据读取

这次是PyTorch的自定义数据读取pipeline模板和相关trciks以及如何优化数据读取的pipeline等。 因为有torch也放人工智能模块了~ 从PyTorch的数据对象类Dataset开始。Dataset在PyTorch中的模块位于utils.data下。 from torch.utils.data import Dataset围绕Dataset对象分别从…
阅读更多...
前端入门必备基础

前端入门必备基础

化繁为简 HTML5要的就是简单、避免不必要的复杂性。HTML5的口号是“简单至上&#xff0c;尽可能简化”。因此&#xff0c;HTML5做了以下改进&#xff1a; 以浏览器原生能力替代复杂的JavaScript代码。 新的简化的DOCTYPE。 新的简化的字符集声明。 简单而强大的HTML5API。…
阅读更多...
[附源码]Python计算机毕业设计SSM基于云数据库的便民民宿租赁系统（程序+LW)

[附源码]Python计算机毕业设计SSM基于云数据库的便民民宿租赁系统（程序+LW)

项目运行 环境配置&#xff1a; Jdk1.8 Tomcat7.0 Mysql HBuilderX&#xff08;Webstorm也行&#xff09; Eclispe&#xff08;IntelliJ IDEA,Eclispe,MyEclispe,Sts都支持&#xff09;。 项目技术&#xff1a; SSM mybatis Maven Vue 等等组成&#xff0c;B/S模式 M…
阅读更多...
《Linux运维实战：MongoDB数据库全量逻辑备份恢复(方案一)》

《Linux运维实战：MongoDB数据库全量逻辑备份恢复(方案一)》

一、备份与恢复方案 mongodump是MongoDB官方提供的备份工具,它可以从MongoDB数据库读取数据,并生成BSON文件,mongodump适合用于备份和恢复数据量较小的MongoDB数据库, 不适用于大数据量备份。 默认情况下mongodump不获取local数据库里面的内容。mongodump仅备份数据库中的文档&…
阅读更多...
回溯算法（1）组合

回溯算法（1）组合

文章目录回溯算法理论77. 组合216. 组合总和17. 电话号码的组合回溯算法理论 回溯算法其实就是递归&#xff0c;只不过递归又分为递去和归来&#xff0c;其中归来便就是回溯。 为什么要使用回溯&#xff1f; 有些问题我们通过暴力解法也很难解决&#xff0c;比如说我们接下来…
阅读更多...
C语言学习之路（高级篇）—— 变量和内存分布（上）

C语言学习之路（高级篇）—— 变量和内存分布（上）

说明&#xff1a;该篇博客是博主一字一码编写的&#xff0c;实属不易&#xff0c;请尊重原创&#xff0c;谢谢大家&#xff01; 数据类型 1) 数据类型概念 什么是数据类型&#xff1f;为什么需要数据类型? 数据类型是为了更好进行内存的管理&#xff0c;让编译器能确定分配…
阅读更多...
04 | 云硬盘的使用方法

04 | 云硬盘的使用方法

前期环境&#xff1a; Ubuntu 0 云硬盘类型 云硬盘类型包括&#xff1a; 高性能云硬盘通用型 SSD 云硬盘SSD 云硬盘增强型 SSD 云硬盘极速型 SSD 云硬盘&#xff0c;仅支持随存储增强型云服务器一同购买&#xff0c;不支持单独购买 1 创建云硬盘 1.1 创建方式 1.1.1 单个…
阅读更多...
第二证券|连拉20CM涨停！防疫新概念股火了！恒生科技指数涨逾5%

第二证券|连拉20CM涨停！防疫新概念股火了！恒生科技指数涨逾5%

周四上午&#xff0c;“新十条”发布后&#xff0c;由于A股商场已反弹一段时刻&#xff0c;两市股指今天早盘接连震动走势&#xff0c;港股在地产、科技、消费等板块带动下&#xff0c;体现更为强势。 A股上证指数早盘在3200点附近持续震动&#xff0c;光伏、化肥、物流、港口等…
阅读更多...
JavaScript内置对象（内置对象、查文档（MDN）、Math对象、日期对象、数组对象、字符串对象）

JavaScript内置对象（内置对象、查文档（MDN）、Math对象、日期对象、数组对象、字符串对象）

目录 JavaScript内置对象 内置对象 查文档 MDN Math对象 Math概述 案例一&#xff1a;封装自己的对象 随机数方法 random() 案例一&#xff1a;猜数字游戏 日期对象 Date 概述 Date()方法的使用 获取日期的总的毫秒形式 案例一&#xff1a;倒计时效果 数组对象 …
阅读更多...
DoltLab本地部署实践

DoltLab本地部署实践

目录引言Dolt是什么&#xff1f;如何本地部署使用DoltLab具体安装步骤安装期间FAQ写在最后其他相关资料引言 自从搞深度学习训练模型以来&#xff0c;一直有个问题困扰着我&#xff1a;训练所用数据集的管理。为什么说这是一个问题呢&#xff1f; 在读研时&#xff0c;我们依据…
阅读更多...
ELK日志分析系统概述及部署

ELK日志分析系统概述及部署

文章目录一、ELK日志分析系统1、概念2、完整日志系统基本特征3、使用ELK的原因4、ELK 的工作原理二、ELK日志分析系统集群部署的操作步骤环境准备&#xff1a;1、 ELK Elasticsearch 集群部署&#xff08;在Node1、Node2节点上操作&#xff09;1.1、更改主机名、配置域名解析、…
阅读更多...
剑指 Offer 53 - I. 在排序数组中查找数字 I

剑指 Offer 53 - I. 在排序数组中查找数字 I

摘要 剑指 Offer 53 - I. 在排序数组中查找数字 I 一、二分查找 1.1 二分查找的分析 由于数组已经排序&#xff0c;因此整个数组是单调递增的&#xff0c;我们可以利用二分法来加速查找的过程。 考虑 target在数组中出现的次数&#xff0c;其实我们要找的就是数组中「第一…
阅读更多...
汇编语言ch2_2 汇编语言中的debug

汇编语言ch2_2 汇编语言中的debug

使用debug 可以完成以下功能&#xff1a; 可以查看 和改变 CPU 中&#xff0c;寄存器的内容&#xff1b;可以查看 和改变内存中的内容&#xff1b;可以将内存中的 机器指令 翻译成汇编指令使用汇编指令 在 内存中 存入 机器指令执行机器指令 首先&#xff0c;启动 Debug,在DO…
阅读更多...
实现数智内控，数据分析创造价值——辽宁烟草智能风险体检系统

实现数智内控，数据分析创造价值——辽宁烟草智能风险体检系统

近两年&#xff0c;烟草行业部分单位围绕中心任务&#xff0c;结合实际&#xff0c;守正创新&#xff0c;开展了许多研究探索。比如&#xff0c;在财务大数据价值挖掘、会计共享中心建设、财务风险预警系统建设等方面做了大量卓有成效的工作。在这样的背景下&#xff0c;辽宁烟…
阅读更多...
DSPE-MAL 磷脂改性马来酰亚胺简介CAS1360858-99-6

DSPE-MAL 磷脂改性马来酰亚胺简介CAS1360858-99-6

DSPE-MAL二硬脂酰磷脂酰乙醇胺改性马来酰亚胺 中文名称&#xff1a;二硬脂酰磷脂酰乙醇胺改性马来酰亚胺 英文名称&#xff1a;DSPE-MAL CAS&#xff1a;1235864-97-7 分子式&#xff1a;C48H86N2NaO11P 分子量&#xff1a;921.16700 外观&#xff1a;白色粉末 DSPE-MAL二…
阅读更多...
2022icpc 济南站 持续补题

2022icpc 济南站 持续补题

链接&#xff1a;Dashboard - 2022 International Collegiate Programming Contest, Jinan Site - Codeforces 签到题&#xff1a;k K. Stack Sort You are given a permutation with nn numbers, a1,a2,…,an(1≤ai≤n,ai≠aj when i≠j). You want to sort these numbers …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023