pytorch基础操作(三)梯度下降(小批量)计算线性回归

1、线性模型

线性假设是指⽬标（房屋价格）可以表⽰为特征（⾯积和房龄）的加权和，如下⾯的式⼦：
price = warea · area + wage · age + b.
其中:
warea和wage 称为权重（weight），权重决定了每个特征对我们预测值的影响。b称为偏置（bias）、偏移量（offset）或截距（intercept）。偏置是指当所有特征都取值为0时，预测值应该为多少。

1、线性模型公式表示

第一种方式:
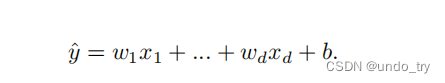
在这里插入图片描述
第二种方式:

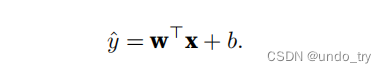
第三种方式:
对于特征集合X，预测值yˆ ∈ Rn 可以通过矩阵-向量乘法表⽰为：

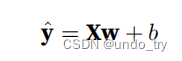
2、loss函数

回归问题中最常⽤的损失函数是平⽅误差函数。
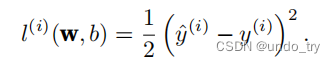
在这里插入图片描述
为了度量模型在整个数据集上的质量，我们需计算在训练集n个样本上的损失均值（也等价于求和）。

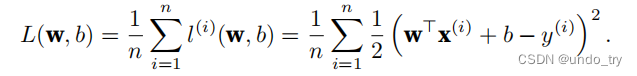
在训练模型时，我们希望寻找⼀组参数（w∗, b∗），这组参数能最⼩化在所有训练样本上的总损失。
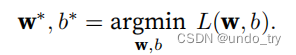
在这里插入图片描述

3、解析解

线性回归的解可以⽤⼀个公式简单地表达出来，这类解叫作解析解（analytical solution）。

⾸先，我们将偏置b合并到参数w中，合并⽅法是在包含所有参数的矩阵中附加⼀列。预测问题是最⼩化∥y − Xw∥^2。
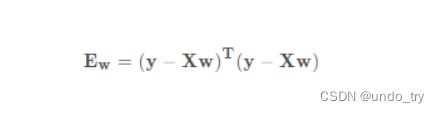
在这里插入图片描述
矩阵求导请参考: 矩阵的求导

（1）通过链式法则求导
先把 y−Xw 看成整体,得到2(y−Xw)，然后计算（y−Xw ）对 w 的导数，其中 y 里面没有包含w ，结果为0，然后−wX 对 w 的导数得到，最终结果就是
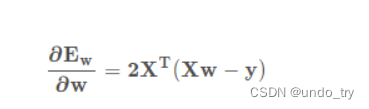
在这里插入图片描述
将损失关于w的导数设为0，得到解析解：

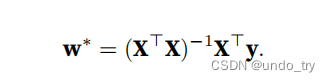
(2)将式子拆开然后每个项求导

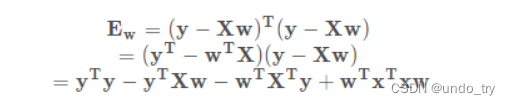
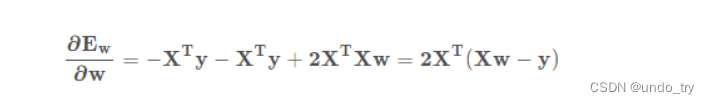
将损失关于w的导数设为0，得到解析解：

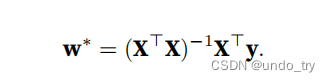
4、随机梯度下降

它通过不断地在损失函数递减的⽅向上更新参数来降低误差。

梯度下降最简单的⽤法是计算损失函数（数据集中所有样本的损失均值）关于模型参数的导数（在这⾥也可以称为梯度）。但实际中的执⾏可能会⾮常慢：因为在每⼀次更新参数之前，我们必须遍历整个数据集。因此，我们通常会在每次需要计算更新的时候随机抽取⼀⼩批样本，这种变体叫做小批量随机梯度下降.

在每次迭代中，我们⾸先随机抽样⼀个小批量，它是由固定数量的训练样本组成的。然后，我们计算小批量的平均损失关于模型参数的导数（也可以称为梯度）。最后，我们将梯度乘以⼀个预先确定的正数η，并从当前参数的值中减掉。
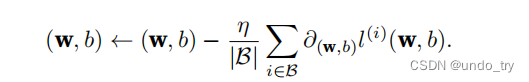
在这里插入图片描述
可以写成下面形式:

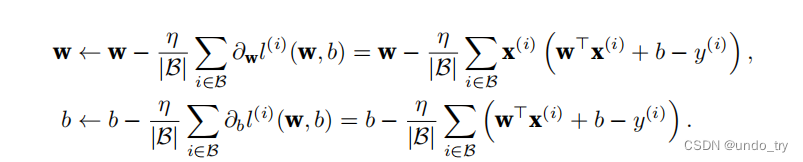
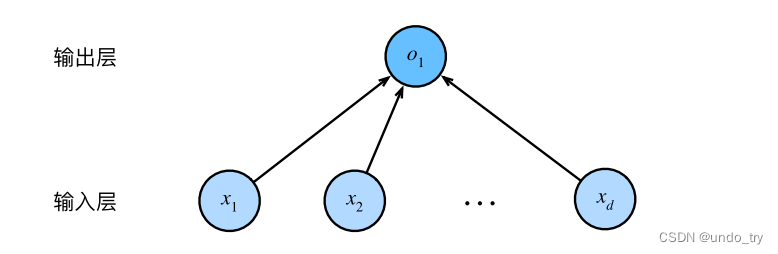
5、线性回归是一个单层的神经网络

在这里插入图片描述

2、手动实现线性回归

(1)、生成数据集

'''
1、生成数据集

我们将根据带有噪声的线性模型构造⼀个⼈造数据集
⽣成⼀个包含1000个样本的数据集，每个样本包含从标准正态分布中采样的2个特征。

我们使⽤线性模型参数w = [2, −3.4]T、b = 4.2 和噪声项ϵ⽣成数据集及其标签
'''

def get_data(w, b, num_samples=1000):
    """⽣成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_samples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X,y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features,labels = get_data(true_w,true_b)

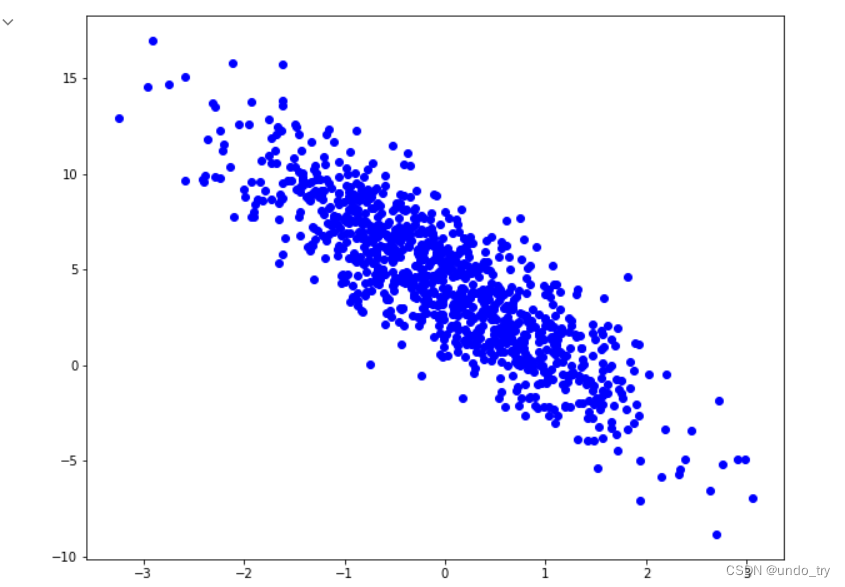
在这里插入图片描述

# 画出散点图
from matplotlib import pyplot as plt
%matplotlib inline

plt.figure(figsize=(10,8))
plt.scatter(features[:, (1)].detach().numpy(), labels.detach().numpy(),color='b')
plt.show()

在这里插入图片描述

(2)、读取数据集

'''
2、读取数据集

该函数接收批量⼤⼩、特征矩阵和标签向量作为输⼊，⽣成⼤⼩为batch_size的⼩批量。每个⼩批量包含⼀组特征和标签
'''
def get_batch_data(batch_size,features,labels):
    # 样本的数目
    num_examples = features.shape[0]
    indices = list(range(num_examples))
    # 洗牌
    random.shuffle(indices)
    for index in range(0, num_examples, batch_size):
        batch_indices = torch.tensor(
            indices[index: min(index + batch_size, num_examples)]
        )
        yield features[batch_indices],labels[batch_indices]

# 我们利⽤GPU并⾏运算的优势，处理合理⼤⼩的“⼩批量”。每个样本都可以并⾏地进⾏模型计算，且
# 每个样本损失函数的梯度也可以被并⾏计算。GPU可以在处理⼏百个样本时，所花费的时间不⽐处理⼀个样本时多太多。

(3)、初始化模型参数

'''
3、初始化模型参数
'''
# 在我们开始用小批量随机梯度下降优化我们的模型参数之前， 我们需要先有一些参数。
w = torch.normal(0,0.01,size=(2,1), requires_grad=True)
b = torch.zeros(1, requires_grad=True)

# 在初始化参数之后，我们的任务是更新这些参数，直到这些参数足够拟合我们的数据。
# 每次更新都需要计算损失函数关于模型参数的梯度。 有了这个梯度，我们就可以向减小损失的方向更新每个参数。

(4)、定义模型

'''
4、定义模型
'''
# 计算线性模型的输出， 我们只需计算输入特征(f{X})和模型权重(w)的矩阵-向量乘法后加上偏置(b)

def line_alg(X, w, b):
    return torch.matmul(X, w) + b

(5)、定义loss函数

'''
5、定义loss函数
'''
# 需要计算损失函数的梯度，所以我们应该先定义损失函数。
def square_loss(y_hat,y):
    return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2

(6)、定义优化算法

'''
6、定义优化算法

尽管线性回归有解析解，但深度学习中的其他模型却没有。 这里我们介绍小批量随机梯度下降。

1、在每一步中，使用从数据集中随机抽取的一个小批量，然后根据参数计算损失的梯度。
2、接下来，朝着减少损失的方向更新我们的参数。


下面的函数实现小批量随机梯度下降更新。
该函数接受模型参数集合、学习速率和批量大小作为输入。

每一步更新的大小由学习速率lr决定。
因为我们计算的损失是一个批量样本的总和，所以我们用批量大小（batch_size） 来规范化步长，这样步长大小就不会取决于我们对批量大小的选择。
'''

# 小批量随机梯度下降
def mini_batch_sgd(params, lr, batch_size):

    # torch.no_grad是一个类一个上下文管理器，disable梯度计算。
    # disable梯度计算对于推理是有用的，当你确认不会调用Tensor.backward()的时候。这可以减少计算所用内存消耗。
    # 这个模式下，每个计算结果的requires_grad=False，尽管输入的requires_grad=True。
    with torch.no_grad():
        for param in params:
            param -= lr * param.grad / batch_size
            param.grad.zero_()

(7)、训练模型

'''
7、训练模型

现在我们已经准备好了模型训练所有需要的要素，可以实现主要的训练过程部分了。
理解这段代码至关重要，因为从事深度学习后， 相同的训练过程几乎一遍又一遍地出现。

1、在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。
2、计算完损失后，我们开始反向传播，存储每个参数的梯度。
3、最后，我们调用优化算法sgd来更新模型参数。


概括⼀下，将执⾏以下循环：
• 初始化参数
• 重复以下训练，直到完成
   计算梯度
   更新参数

在每个迭代周期（epoch）中，我们使用get_batch_data函数遍历整个数据集， 并将训练数据集中所有样本都使用一次（假设样本数能够被批量大小整除）。
这里的迭代周期个数num_epochs和学习率lr都是超参数，分别设为3和0.03。

设置超参数很棘手，需要通过反复试验进行调整，我们现在忽略这些细节。
'''
# 超参数，学习率
lr = 0.03
# 迭代周期
num_epochs = 3
# 模型
net = line_alg
# loss
loss = square_loss


for epoch in range(num_epochs):
    # 在每个迭代周期（epoch）中，我们使用get_batch_data函数遍历整个数据集， 并将训练数据集中所有样本都使用一次
    for X,y in get_batch_data(batch_size,features,labels):
        # X和y的小批量损失
        l = loss(net(X,w, b), y)
        # 因为l的shape形状是(batch_size, 1)而不是一个标量.l中所有的元素被加到一起
        # 并以此计算关于[w,b]的梯度
        l.sum().backward()

        # 使用参数的梯度更新参数
        mini_batch_sgd([w, b], lr, batch_size)

    with torch.no_grad():
         train_l = loss(net(features, w, b), labels)
         print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')

在这里插入图片描述

2、pytorch线性回归

(1)、生成数据集

'''
如何通过使⽤深度学习框架来简洁地实现线性回归模型?


从0开始线性回归中，我们只运⽤了：
（1）通过张量来进⾏数据存储和线性代数；
（2）通过⾃动微分来计算梯度。
实际上，由于数据迭代器、损失函数、优化器和神经⽹络层很常⽤，现代深度学习库也为我们实现了这些组件。
'''
import torch
'''
1、生成数据集
'''

def get_data(w, b, num_samples=1000):
    """⽣成y=Xw+b+噪声"""
    X = torch.normal(0, 1, (num_samples, len(w)))
    y = torch.matmul(X, w) + b
    y += torch.normal(0, 0.01, y.shape)
    return X,y.reshape((-1, 1))

true_w = torch.tensor([2, -3.4])
true_b = 4.2
features,labels = get_data(true_w,true_b)

(2)、读取数据集

'''
2、读取数据集

我们可以调⽤框架中现有的API来读取数据。

我们将features和labels作为API的参数传递，并通过数据迭代器指定batch_size。
此外，布尔值is_train表⽰是否希望数据迭代器对象在每个迭代周期内打乱数据。
'''
import numpy as np
from torch.utils import data

batch_size = 10

def get_batch_data(data_arrays,batch_size,is_train=True):
    """构造一个pytorch读取器"""
    dataset = data.TensorDataset(*data_arrays)
    return data.DataLoader(dataset, batch_size, shuffle=is_train)

# for X, y in get_batch_data((features, labels),batch_size):
#          print(X, '\n', y)
#          break

# 这⾥我们使⽤iter构造Python迭代器，并使⽤next从迭代器中获取第⼀项。
data_iter = get_batch_data((features, labels),batch_size)
next(iter(data_iter))

在这里插入图片描述

(3)、定义模型

'''
3、定义模型

我们⾸先定义⼀个模型变量net，它是⼀个Sequential类的实例。
Sequential类将多个层串联在⼀起。

当给定输⼊数据时，Sequential实例将数据传⼊到第⼀层，然后将第⼀层的输出作为第⼆层的输⼊，以此类推。

在下⾯的例⼦中，我们的模型只包含⼀个层，因此实际上不需要Sequential。
但是由于以后⼏乎所有的模型都是多层的，在这⾥使⽤Sequential会让你熟悉“标准的流⽔线”。

这⼀单层被称为全连接层（fully-connected layer），因为它的每⼀个输⼊都通过矩阵-向量乘法得到它的每个输出。
'''
# 在PyTorch中，全连接层在Linear类中定义。
# 值得注意的是，我们将两个参数传递到nn.Linear中。
# 第1个指定输⼊特征形状，即2
# 第2个指定输出特征形状，输出特征形状为单个标量，因此为1。
from torch import nn


net = nn.Sequential(nn.Linear(2, 1))

(4)、初始化模型参数

'''
4、初始化模型参数

在使⽤net之前，我们需要初始化模型参数。如在线性回归模型中的权重和偏置。深度学习框架通常有预定
义的⽅法来初始化参数。

在这⾥，我们指定每个权重参数应该从均值为0、标准差为0.01的正态分布中随机采样，偏置参数将初始化为零。


'''

# 正如我们在构造nn.Linear时指定输⼊和输出尺⼨⼀样，现在我们能直接访问参数以设定它们的初始值。
# 我们通过net[0]选择⽹络中的第⼀个图层，然后使⽤weight.data和bias.data⽅法访问参数。
# 我们还可以使⽤替换⽅法normal_和fill_来重写参数值。

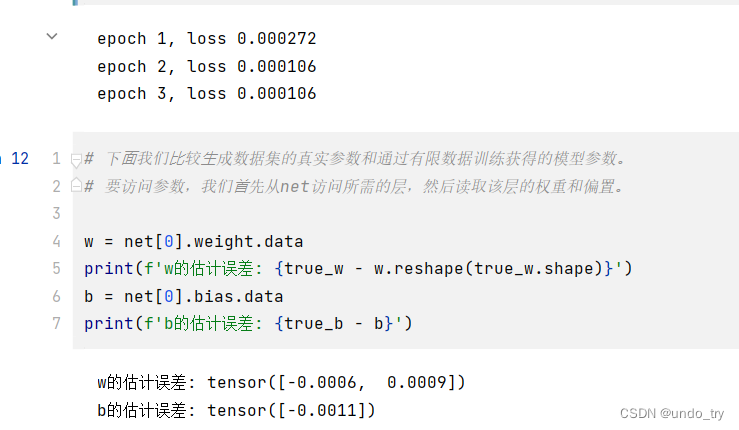
net[0].weight.data.normal_(0, 0.01)
net[0].bias.data.fill_(0)

(5)、定义loss函数

'''
5、定义loss函数

计算均⽅误差使⽤的是MSELoss类，也称为平⽅L2范数。默认情况下，它返回所有样本损失的平均值。
'''
loss = nn.MSELoss()

(6)、定义优化算法

'''
6、定义优化算法

⼩批量随机梯度下降算法是⼀种优化神经⽹络的标准⼯具，PyTorch在optim模块中实现了该算法的许多变种。

当我们实例化⼀个SGD实例时，我们要指定优化的参数（可通过net.parameters()从我们的模型中获得）以及优化算法所需的超参数字典。
⼩批量随机梯度下降只需要设置lr值，这⾥设置为0.03。
'''
trainer = torch.optim.SGD(net.parameters(), lr=0.03)

(7)、模型的训练

'''
7、模型的训练


通过深度学习框架的⾼级API来实现我们的模型只需要相对较少的代码。

我们不必单独分配参数、不必定义我们的损失函数，也不必⼿动实现⼩批量随机梯度下降。
当我们需要更复杂的模型时，⾼级API的优势将⼤⼤增加。

当我们有了所有的基本组件，训练过程代码与我们从零开始实现时所做的⾮常相似。

回顾⼀下：
在每个迭代周期⾥，我们将完整遍历⼀次数据集（train_data），不停地从中获取⼀个⼩批量的输⼊和相应的标签。
对于每⼀个⼩批量，我们会进⾏以下步骤:
• 通过调⽤net(X)⽣成预测并计算损失l（前向传播）。
• 通过进⾏反向传播来计算梯度。
• 通过调⽤优化器来更新模型参数。

'''

# 为了更好的衡量训练效果，我们计算每个迭代周期后的损失，并打印它来监控训练过程。
num_epochs = 3

for epoch in range(num_epochs):
    for X,y in data_iter:
        l = loss(net(X), y)
        trainer.zero_grad()
        l.backward()
        trainer.step()

    l = loss(net(features), labels)
    print(f'epoch {epoch + 1}, loss {l:f}')