【C语言程序设计】实验 6

news2024/11/17 7:38:15

1. 无理数e

2. 平面镜反数

3. 整数分解质因数

4. 素数回文

5. 阶乘和数

6. 输出星号图案

7. 验证哥德巴赫猜想

1. 无理数e

【问题描述】输入一个正整数，由下式e=1+1/1!+1/2!+...+1/n!求无理数e，保留9位小数。
【输入形式】一个正整数n(<=20)。
【输出形式】e=1+1/1!+1/2!+...+1/n!
【样例1输入】1
【样例1输出】2.000000000

【样例2输入】5
【样例2输出】2.716666667

#include<stdio.h>
int main(){
   int n;
   double e,s1=1,s2=1;
   scanf("%d",&n);
   for(int i=1;i<=n;i++){
s1*=i;
       s2+=1/s1;
   }
   printf("%.9f",s2);
   return 0;
/*   int x;
   scanf("%d",&x);
   double e=1,fact=1;
   long n=0;
   do{
       n++;
       fact*=n;
       e=e+1/fact;
   }while(n<x);
   printf("%.9f",e);
   return 0;
   */
}

2. 平面镜反数

【问题描述】求二位正整数的平方镜反数。平方镜反数是指该数的平方与该数的反序数的平方互为反序数。如122＝144，212＝441。则12就是一个平方镜反数。

【输入形式】无
【输出形式】每对数占一行，加一括号。如(13,31)。注意，符号要英文状态。

【样例输入】无
【样例输出】

(11,11)
(12,21)
(13,31)
(21,12)
(22,22)
(31,13)

#include<stdio.h>
#include<math.h>
int main(){
   int i,j,n,m,t;
   for(i=10;i<100;i++){
       j=i%10*10+i/10;
       m=i*i;
       n=j*j;
       t=0;
       while(n){
           t=t*10+n%10;
           n/=10;
       }
       if(m==t){
           printf("(%d,%d)\n",i,j);
       }
   }
   return 0;
}

3. 整数分解质因数

【问题描述】从键盘输入一个整数，将整数分解质因数。例如，输入90，输出90=2*3*3*5。

【输入形式】一个整数n
【输出形式】从小到大输出分解的质因数乘积。
【样例1输入】90
【样例1输出】2*3*3*5

【样例说明】90=2*3*3*5。参见课本例5.28。

【样例2输入】2
【样例2输出】2

【样例3输入】19
【样例3输出】19

#include<stdio.h>
int main(){
   int i,n;
   scanf("%d",&n);
   if(n==2){
       printf("2\n");
   }else{
       i=2;
   do{
       if(n%i==0){
           printf("%d*",i);
           n=n/i;
       }else{
           i++;
       }
   }while(n!=i);
   printf("%d\n",n);
   }
   return 0;
}

4. 素数回文

【问题描述】找出既是素数又是回文的所有三位数。

【输入形式】无
【输出形式】每行5个数，各占8位。

【样例输入】无
【样例输出】

101     131     151     181     191
313     353     373     383     727
757     787     797     919     929

#include<stdio.h>
int main(){
   int i,j,k,m,count=0;
   for(i=100;i<1000;i++){
       k=0;
       for(j=2;j<=i/2;j++){
           if(i%j==0){
               k++;
       }
       }
       m=i;
       if(k==0&&(m/100==m%10)){
           printf("%-8d",i);
           count++;
       if(count%5==0){
           printf("\n");
       }
       }
   }
   return 0;
}

5. 阶乘和数

【问题描述】一个正整数如果等于组成它的各位数字的阶乘之和，则该正整数称为阶乘和数。例如正整数145，1!+4!+5!等于145，因此145就是一个阶乘和数。找出1-200000范围内的阶乘和数，每行二个数，各占8位。

【输入形式】无
【输出形式】
【样例输入】
【样例输出】

1 2
145 40585

#include<stdio.h>
int main(){
   int i,j,n,s,k,t,c=0;
   for(i=1;i<200000;i++){
       k=i;
       s=0;
       while(k){
           t=1;
           n=k%10;
           for(j=2;j<=n;j++){
               t*=j;
           }
           s+=t;
           k/=10;
       }
       if(s==i){
           printf("%8d",i);
           c++;
       if(c%2==0)
           printf("\n");
       }
   }
   return 0;
}

6. 输出星号图案

【问题描述】输入整数n(1<=n<=10)，输出以下格式的2n-1行图案。

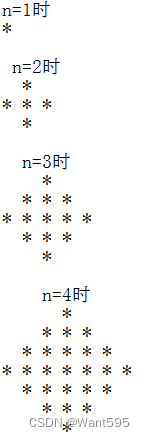
【输入形式】一个整数n。
【输出形式】2n-1行图案

【样例输入】3

【样例输出】

#include<stdio.h>
int main(){
   int i,j,k,n;
   scanf("%d",&n);
   for(i=1;i<=n;i++){
for(j=n-i;j>0;j--){
   printf(" ");
       }
       for(j=0;j<2*i-1;j++){
           printf("*");
       }
       printf("\n");
   }
   for(i=n-1;i>0;i--){
       for(j=0;j<n-i;j++){
           printf(" ");
       }
       for(j=2*i-1;j>0;j--){
           printf("*");
       }
       printf("\n");
   }
   return 0;
}

7. 验证哥德巴赫猜想

【问题描述】验证哥德巴赫猜想：任何一个大于5的偶数均可表示为两个素数之和。输入6～100之间的一个偶数，输出它表示成两个素数之和的全部形式。素数指只能被1和自身整除的正整数，1不是素数，2是素数。
【输入形式】一个大于5的偶数。
【输出形式】输出这个数表示成两个从小到大的素数之和的全部形式，一个形式占一行。

【样例1输入】6
【样例1输出】6=3+3

【样例2输入】60
【样例2输出】

60=7+53
60=13+47
60=17+43
60=19+41
60=23+37
60=29+31

#include<stdio.h>
#include<math.h>
int main(){
int n,i;
scanf("%d",&n);
for(i=2;i<=n/2;i++){
   int j,k,m=sqrt(i),s=sqrt(n-i);
   for(j=2;j<=m;j++){
       if(i%j==0)
       break;
       }
       for(k=2;k<=n;k++){
           if((n-i)%k==0)
           break;
       }
       if(j>m&&k>s){
           printf("%d=%d+%d\n",n,i,n-i);
       }
   }
   return 0;
}