回溯算法理论

回溯算法其实就是递归，只不过递归又分为递去和归来，其中归来便就是回溯。

为什么要使用回溯？
有些问题我们通过暴力解法也很难解决，比如说我们接下来要讲的这几道题，他们的共性是我们都需要大量的for循环来遍历某个序列，但是其中for循环的次数随着条件的改变而改变，通过暴力，我们很难找到某一个问题的通解。

注意：回溯本身就是递归，而递归就是不断穷举所有可能性的过程，所以，一般情况下，我们应该能使用迭代就使用迭代，迫不得已再使用递归（回溯）来解决问题。

---

回溯算法的理解：
因为回溯一般解决的都是在一个大的集合中寻找子集的情况，所以我们可以把这个大的集合看作一个二叉树，回溯就是遍历二叉树，找到所有叶子节点的过程。
集合的大小： 构成二叉树的宽度（集合越大，二叉树就越宽）
寻找或操作的次数：构成二叉树的深度，也是回溯的深度。

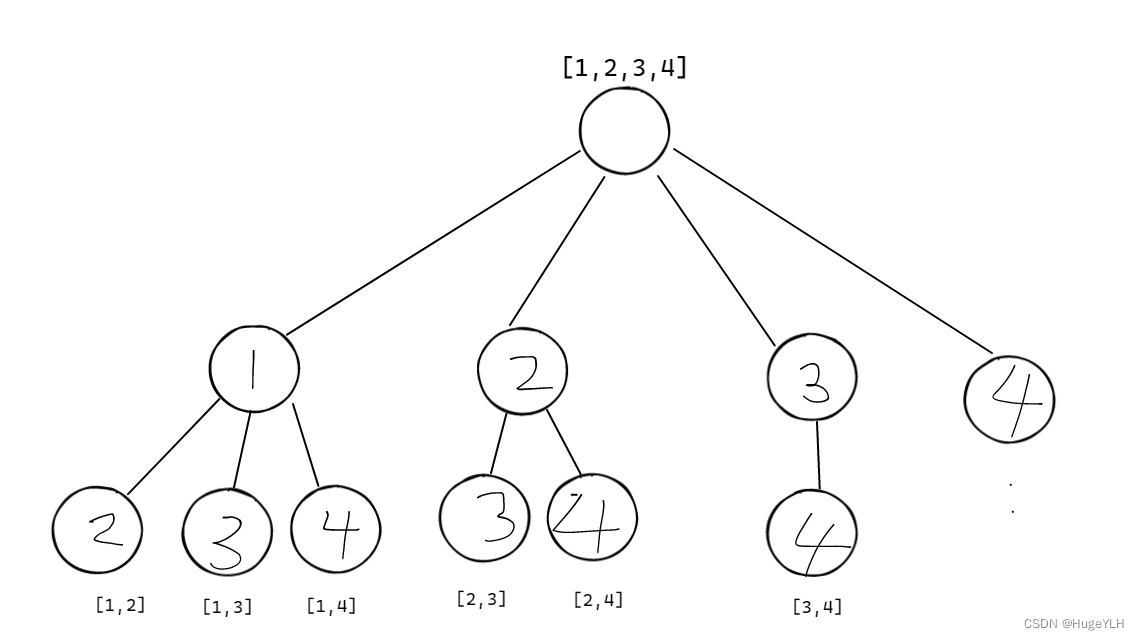
假设我们的集合大小为4，根据集合的初始位置得到子集和的初始位置，进而操作得到子集和。

---

回溯模板：

void dfs()
{
	if (符合某种条件)
	{
		进行记录操作（在一般的回溯过程中，我们需要记录符合条件的子集合）
		return;
	}
	for (遍历本层的各个节点)
	{
		对于一个未被操作的节点：记录下此节点，把他当作一个新的根节点，遍历其子树
		dfs();//进入递归
		到达了叶子节点并且操作完成，弹出此节点，继续遍历下一节点
	}
}

大的圆圈表示我们的第一层for循环的遍历过程，小的圆圈表示我们每次递归后的子for循环。

---

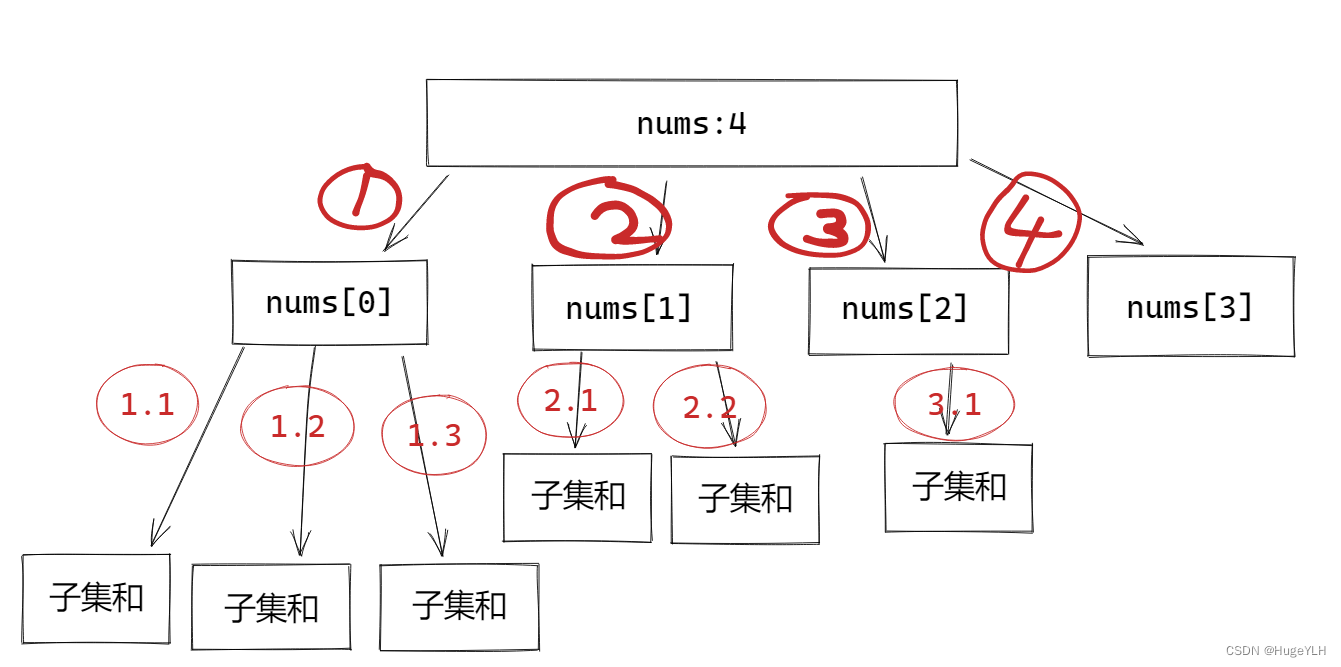
总结：回溯法解决的问题都可以抽象为树形结构

77. 组合

力扣传送门：
https://leetcode.cn/problems/combinations/?envType=study-plan&id=suan-fa-ru-men&plan=algorithms&plan_progress=1syarli

题目：

列出所有 [1，n]的长度为k的子集和。

这道题算是我们回溯算法的入门题目，当我们使用for循环时，我们需要大量的嵌套for循环，甚至无法暴力解决，因此我们只能使用回溯的算法解决。

本题回溯算法：就是在一个for循环中进入递归，然后隐式的调用 n 个for循环，其实就是穷举出所有可能性。

---

class Solution {
private:
    vector<vector<int>> res;//存储最后的结果（所有的叶子节点）
    vector<int> temp;   //存储一个叶子节点（子集和）
public:
    void dfs(int n,int k,int startIdx)
    {
    	//当表示叶子节点的数组大小为k时，说明找到了某个子集和，存储进结果中
        if (temp.size()==k)
        {
            res.emplace_back(temp);
            //到达了叶子节点，递归终止
            return;
        }
        //依次遍历每一层的同级节点（看图）
        for (int i=startIdx;i<=n;i++)
        {
        	//存储每一个子树的根节点
            temp.push_back(i);
            //子树进入递归，再次重复上面的操作
            dfs(n,k,i+1);
            //返回上一层，弹出最后的节点
            temp.pop_back();
            //然后接着遍历同级的下一节点
        }
    }
    vector<vector<int>> combine(int n, int k) {
        dfs(n,k,1);
        return res;
    }
};

---

剪枝操作：
看图：

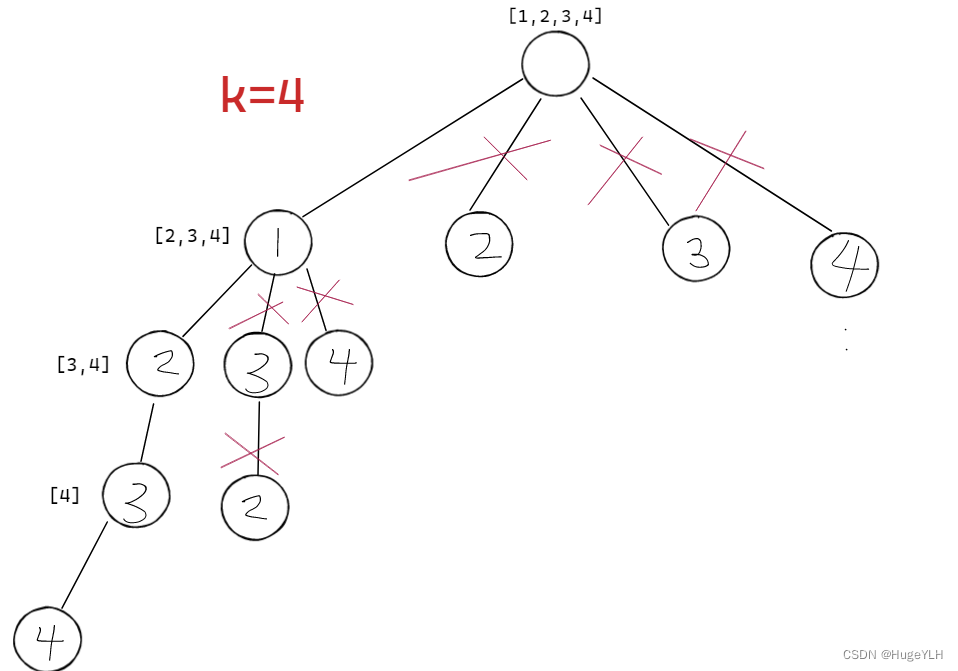
当我们要取4个数字时，先看第二层：由于我们在取得1之后可以在取3个，因此节点1满足这个情况，但是节点2，3，4都不能再取得三个数字，所以可以直接退出此循环；节点1中取三个数字后的情况也是如此。

因此，剪枝（递归优化）的代码：

class Solution {
private:
    vector<vector<int>> res;    //存放总的结果
    vector<int> temp;           //存放一次的结果
public:
    void dfs(int n,int k,int startIdx)
    {
        if (temp.size()==k)
        {
            res.emplace_back(temp);  //将这一次的结果存放进整个结果中
            return;
        }
        for (int i=startIdx;i<=n-(k-temp.size())+1;i++)
        {
            temp.push_back(i);
            dfs(n,k,i+1);
            temp.pop_back();
        }
    }
    vector<vector<int>> combine(int n, int k) {
        dfs(n,k,1);
        return res;
    }
};

---

216. 组合总和

力扣传送们：
https://leetcode.cn/problems/combination-sum-iii/description/

本题与上一题基本一致，就是把用回溯模拟的树的深度增大到了9，因为是从[1,9]中随机抽取，所以我们的树应该深度为9，

class Solution {
private:
    vector<vector<int>> res;
    vector<int> temp;
public:
    void dfs(int k,int n,int startIdx)
    {
    	//计算总和
        int sum=accumulate(temp.begin(),temp.end(),0);
        //判断总和是否相等，并且元素个数是否为k个
        if (sum==n && k==temp.size())
        {
            res.emplace_back(temp);
            return;
        }
        //for循环：横向遍历
        //递归：纵向递归
        for (int i=startIdx;i<=9;i++)
        {
            temp.push_back(i);
            dfs(k,n,i+1);
            temp.pop_back();
        }
    }
    vector<vector<int>> combinationSum3(int k, int n) {
        dfs(k,n,1);
        return res;
    }
};

17. 电话号码的组合

力扣传送门：
https://leetcode.cn/problems/letter-combinations-of-a-phone-number/solutions/

class Solution {
private:
    vector<string> res;
    string temp;
    unordered_map<char, string> phoneMap{
            {'2', "abc"},
            {'3', "def"},
            {'4', "ghi"},
            {'5', "jkl"},
            {'6', "mno"},
            {'7', "pqrs"},
            {'8', "tuv"},
            {'9', "wxyz"}
        };
public:
    void dfs(int index,string& s)
    {
        if (s.size()==index)
        {
            //长度相同
            res.emplace_back(temp);
            return;
        }
        //取出子字符串
        char digit=s[index];
        string lit_str=phoneMap[digit];
        for (int i=0;i<lit_str.size();i++)
        {
            temp.push_back(lit_str[i]);
            dfs(index+1,s);
            temp.pop_back();
        }
    }
    vector<string> letterCombinations(string digits) {
        if (digits.size() == 0) {
            return res;
        }
        dfs(0,digits);
        return res;
    }
};