摘要

剑指 Offer 53 - I. 在排序数组中查找数字 I

一、二分查找

1.1 二分查找的分析

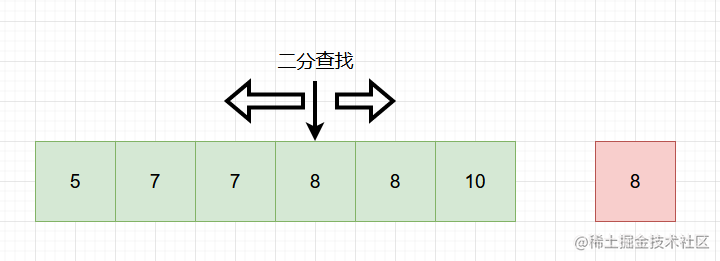
由于数组已经排序，因此整个数组是单调递增的，我们可以利用二分法来加速查找的过程。

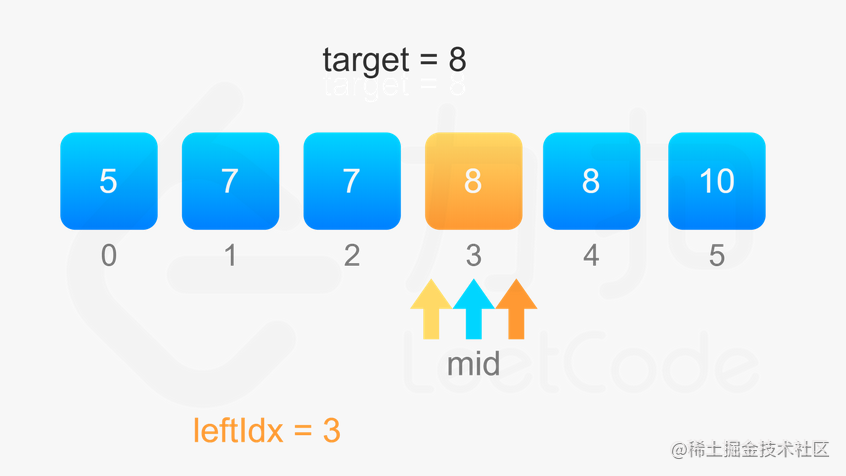
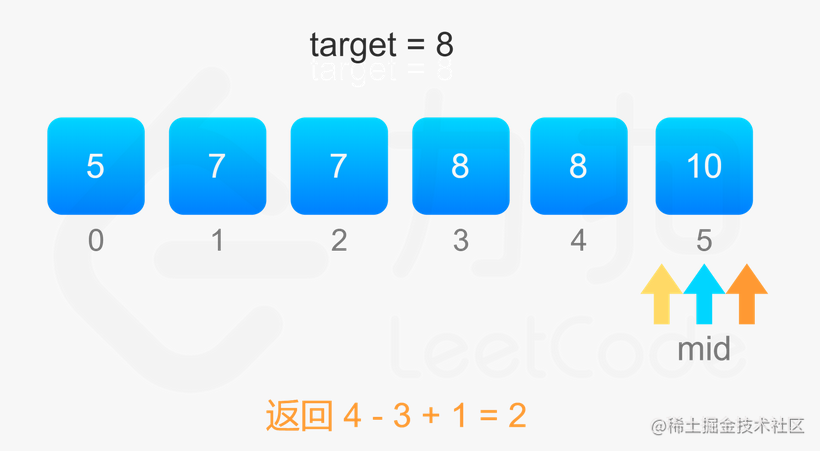
考虑 target在数组中出现的次数，其实我们要找的就是数组中「第一个等于 target的位置」（记为 leftIdx）和「第一个大于 target的位置减一」（记为 rightIdx）。当 target在数组中存在时，target在数组中出现的次数为 rightIdx−leftIdx+1。

二分查找中，寻找 leftIdx即为在数组中寻找第一个大于等于 target的下标，寻找 rightIdx即为在数组中寻找第一个大于 target的下标，然后将下标减一。两者的判断条件不同，为了代码的复用，我们定义 binarySearch(nums, target, lower) 表示在 nums 数组中二分查找 target 的位置，如果 lower 为 true，则查找第一个大于等于 target 的下标，否则查找第一个大于 target的下标。

最后，因为 target 可能不存在数组中，因此我们需要重新校验我们得到的两个下标 leftIdx 和 rightIdx，看是否符合条件，如果符合条件就返回 rightIdx−leftIdx+1，不符合就返回 0。

1.2 二分查找的复杂度

• 时间复杂度： O(log⁡n) ，其中 n 为数组的长度。二分查找的时间复杂度为 O(log⁡n)，一共会执行两次，因此总时间复杂度为 O(log⁡n)。

• 空间复杂度：O(1) 。只需要常数空间存放若干变量。

1.3 code 示例

public int search3(int[] nums, int target) {
    int len = nums.length;
    if (len == 0) {
        return 0;
    }
    int firstposition = findFirstPostition(nums, target);
    if (firstposition == -1) {
        return 0;
    }
    int lastposition = findLastPostition(nums, target);
    System.out.println(firstposition);
    System.out.println(lastposition);
    return lastposition - firstposition + 1;
}

private int findLastPostition(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while (left < right) {
        int mid = left+(right-left+1)/2;
        if (nums[mid] <= target) {
            left = mid;
        } else {
            right = mid-1;
        }
    }
    return left;
}

private int findFirstPostition(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1;
    while (left < right) {
        int mid = left+(right-left)/2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else {
            right = mid;
        }
    }
    if (nums[left] == target) {
        return left;
    }
    return -1;
}

/**
 * @description 利用数组有序 利用二分查找的 log(n)  空间是 O(0)
  * @param: nums
 * @param: target
 * @date: 2022/12/8 11:27
 * @return: int
 * @author: xjl
*/
public int search2(int[] nums, int target) {
    int count=0;
    int index = Arrays.binarySearch(nums, target);
    if (index<0){
        return 0;
    }else {
        int left=index-1;
        while (left>=0){
            if(nums[left]==target){
                count++;
                left--;
            }else {
                break;
            }
        }
        int right=index+1;
        while (right<nums.length){
            if(nums[right]==target){
                count++;
                right++;
            }else {
                break;
            }

        }
        return count+1;
    }
}

二、暴力方法

直接遍历就可以知道目标值的次数。但是这样的做法太过于暴力和简单了。本题目就是考察顺序数组的二分查询特点。

1.3 复杂度分析

• 时间复杂度： O(n) ，其中 n为数组的长度。

• 空间复杂度：O(1) 。只需要常数空间存放若干变量。

2.3 code 示例

/**
 * @description 查询目标的数字在的次数
  * @param: nums
 * @param: target
 * @date: 2022/12/8 11:25
 * @return: int
 * @author: xjl
*/
public int search(int[] nums, int target) {
    int count=0;
    for (int i:nums){
        if (i==target){
            count++;
        }
    }
    return count;
}

博文参考