损失函数是如何设计出来的?
可以直接观看b站优质博主的视频,该博主讲的也是非常通透。劝大家直接去看视频,我这只是做一个学习笔记。
https://www.bilibili.com/video/BV1Y64y1Q7hi/?spm_id_from=333.788&vd_source=e13ed5ec556f20f3f3c29fffcc596924
交叉熵损失函数:https://www.bilibili.com/video/BV15V411W7VB/?spm_id_from=333.788&vd_source=e13ed5ec556f20f3f3c29fffcc596924
从学习神经网络的历程中,我们知道,通过使用梯度下降法来进行反向传播,来迭代更新网络的参数。在了解梯度下降算法之前,我们需要了解一下损失函数。(具体梯度下降如何计算,我会在后续的博客中进行更新。)
因此,现在有了第一个问题:科学家们是如何设计出来损失函数的呢?
我们已经知道,神经网络无非就是一堆线性映射函数,加一些激活函数来构成,结构非常简单,但是却能表现出智能。我们学习神经网络的优化过程中,总是绕不开一个问题,那就是损失函数。这个问题似乎很重要,但似乎又总是被我们忽略。吴恩达在他的课程里已经写了很多损失函数,让我印象深刻的有两个,第一个是最基础的MSE损失函数,另外一个就是交叉墒CE损失函数。但为什么要这么设计呢?
实际上,当我们在判断一张图片是不是猫时候,我们大脑中似乎是有一个分布的,那就是猫应该是什么样子的。而神经网络在学习时,它学习参数也存在一个分布。学习的实质是想让人脑中的分布与神经网络的学习到的分布达到一致。当然了,我们可以想象到的是,这两个分布差别越小,那么神经网络可能也就越标准。但关键是,这两个分布说不清道不明,不知道这两个概率模型应该如何比较。
那么接下来,我们就要想想,该如何比较这两个分布呢?神经网络的计算标准,和你的那个标准,如何进行一个定量的表达呢?如果是比较两个圆(直接比较半径),比较两个正态分布(比较方差),这都比较容易。当然你不知道损失函数怎么构造,似乎也没关系。你依然可以取跑代码,实现你个人的网络,但总有一种不通透的感觉。那么我们需要更好的理解损失函数。
现在我们用一个神经网络来模拟一下,伸进网络如何判断猫的?
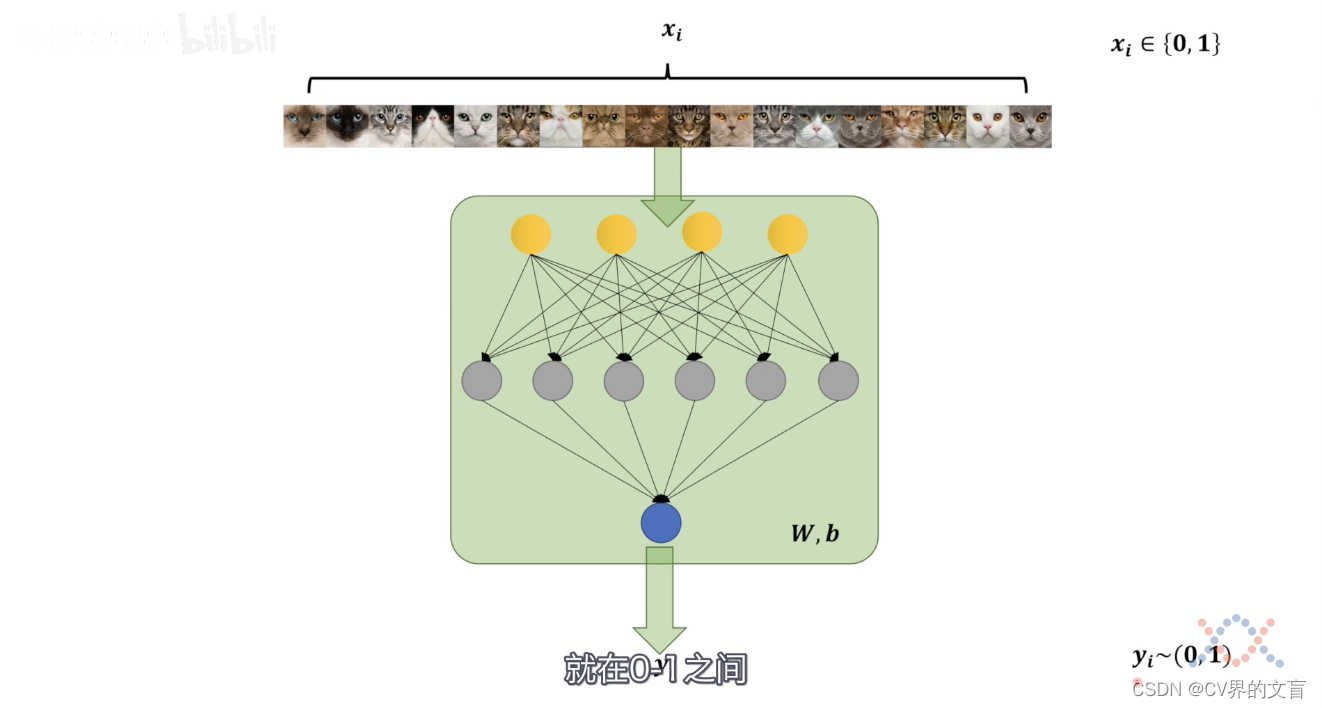
可以看到,我们中间这一对神经元就代表了我们的神经网络,我们先不用去管,这些神经元的设计,你就暂时想象成一个编码器,这个编码器可以是任何你知道的能够提取特征的东西,比如,多层感知机,CNN,RNN,Transformer等等,那么蓝色的点,表示网络最终输出的结果,这个W和b呢,抽象成网络的参数。也就是网络要学习的东西。
一个符合人类直觉的比较就是,拿神经网络输出的这个结果,直接与人类判断的结果进行比较,如果一样,那么就学的是对的,如果不一样,我们就调整参数,让他变得一样,对吧。那么这样的一个过程,用数学表达式可以写成:
| X_i-Y_i |
如果是一百张,一千张呢?那么就对着个公式进行求和:那我们肯定是想要最小化这个值对吧?那就加上min表示我要最小化这个函数。
min (Sum ( | X_i-Y_i | ))
当然这就是最简单的损失函数了。但此时出现一个问题就是:这样造出来一个函数做损失函数,它不可导啊!那不可导怎么反向求导,进行梯度下降来更新参数呢?那么最简单的就是把这个式子加一个平方。这就是MSE了。相信大家对这个已经很熟悉了。
视频的博主还形象的解释了概率和似然的关系,似然是什么意思呢?实际上就是概率的反向应用。比如,我们现在已经知道,质地均匀的硬币,投出去之后,它正面反面出现的概率各是0.5,那么如果,我们不知道这个概率分布呢?也就是说,这个0.5是理念世界的概率分布。而现实世界,你只抛十次硬币,他可能不会5次正面五次反面。
也就是说,你给神经网络一堆图片,实现神经网络是不知道这个理念世界的数据是如何分布的,也就是说,事件已经发生了,我们要从这些已知的事件中去估计这个真实的分布,这就是神经网络在做的事情。理念世界概率分布指导了现实世界事件发生的情况,但根据现实世界的发生情况,也可以反推理念世界的概率分布。也就是结果已知,反向推算概率模型的过程,就是似然的一个过程。反推过来的这个概率分布,就是似然值。似然值总是和真实值是有差异的,但是我们想要一个最大可能性的似然值,就是最大似然估计。这个值就是最接近真实分布的那个概率。
从连乘转化为连加,实际上就是添加了一个对数运算,最后转换为交叉墒损失。
由于公式难打,这里就不继续进行解释了,达不到视频理解的效果。