目录
题目描述
输入描述
输出描述
用例
题目解析
算法源码
题目描述
有M(1<=M<=10)个端口组,
每个端口组是长度为N(1<=N<=100)的整数数组,
如果端口组间存在2个及以上不同端口相同,则认为这2个端口组互相关联,可以合并。
第一行输入端口组个数M,再输入M行,每行逗号分隔,代表端口组。
输出合并后的端口组,用二维数组表示。
输入描述
第一行输入一个数字M
第二行开始输入M行,每行是长度为N的整数数组,用逗号分割
输出描述
合并后的二维数组
用例
| 输入 | 4 4 2,3,2 1,2 5 |
| 输出 | [[4],[2,3,2],[1,2],[5]] |
| 说明 | 仅有一个端口2相同,不可以合并。 |
| 输入 | 3 2,3,1 4,3,2 5 |
| 输出 | [[1,2,3,4],[5]] |
| 说明 | 无 |
| 输入 | 6 10 4,2,1 9 3,6,9,2 6,3,4 8 |
| 输出 | [[10],[1,2,3,4,6,9],[9],[8]] |
| 说明 | 无 |
题目解析
这道题看上去平平无奇,但是如果看用例得话,似乎大有深意。
比如用例3,如果只进行一次匹配得话,则只有3,6,9,2和6,3,4可以合并,但是用例结果显示,3,6,9,2和6,3,4合并后得结果还要继续和4,2,1合并,这就意味着一个双重for是不够的,比如
matrix = [arr1, arr2, arr3, arr4, arr5]
我们首先基于arr1,将arr1和它后面的arr2合并,如果可以合并,则先将arr1合并入arr2,再将arr1.length = 0 ,然后结束本轮,如果不可以合并,则接着分别和arr3、arr4、arr5合并。
然后基于arr2,将arr2和它后面的arr3合并,同上逻辑。
但是我们需要注意的是,如果第一轮时 arr1无法和其他端口组合并,那么arr1将保留,然后第二轮arr2和尝试和其他端口组合并,比如arr2和arr3可以合并,且合并后的arr3和arr1是可以合并的。
那么双重for的逻辑可以支持arr3再回头和arr1合并吗?答案是不可以的,因为外层for循环是不可逆的,因此我们必须再在双重for外面套一层循环。
我觉得使用while比较好,我们可以定义一个flag变量,初始为true,作为while的循环条件,当进入while循环后,立即将flag=false,然后进行上面双重for逻辑,只要有端口组发生合并,则将flag=true,如果双重for结束了,也没有端口组发生合并,那么就说明真的没有端口组可以合并了,因此flag保持为false,while结束。
这是端口组合并的大逻辑。
接下来就是端口组什么条件下合并?
如果端口组间存在2个及以上不同端口相同,则认为这2个端口组互相关联,可以合并。
按照题目意思,只要两个端口组之间有>=2个的相同端口,即可合并。
此时,我们应该尽量让合并判断的时间复杂度降低,因为外面已经有三层循环嵌套了。
这里,我们可以先将两个尝试合并的端口组,先进行升序排序,然后一层循环即可统计出相同端口的对数
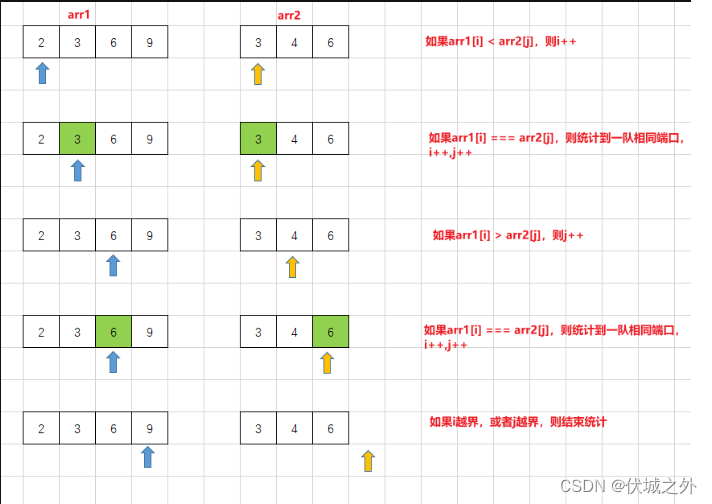
这样的话,就可以用O(n)的时间复杂度来判断两个端口组是否可以合并了。
接下来就是具体合并策略了,根据用例3可以发现,合并后的端口组是去重的,升序的,因此我们也要对合并后的端口进行去重升序。
但是,根据用例1输出的2,3,2来看,未合并的端口组是不能去重和排序的。
最终时间复杂度可以达到 O(m^3 * n),其中1<=m<=10,1<=n<=100,差不多10万次循环,还可以接受。
算法源码
/* JavaScript Node ACM模式 控制台输入获取 */
const readline = require("readline");
const rl = readline.createInterface({
input: process.stdin,
output: process.stdout,
});
const lines = [];
let m;
rl.on("line", (line) => {
lines.push(line);
if (lines.length === 1) {
m = lines[0] - 0;
}
if (m && lines.length === m + 1) {
lines.shift();
const matrix = lines.map((line) => line.split(",").map(Number));
console.log(getResult(matrix));
lines.length = 0;
}
});
function getResult(matrix) {
let flag = true;
while (flag) {
flag = false;
for (let i = matrix.length - 1; i >= 1; i--) {
if (matrix[i].length > 1) {
for (let j = i - 1; j >= 0; j--) {
if (matrix[j].length > 1) {
if (canMerge(matrix[i], matrix[j])) {
matrix[j] = [...new Set([...matrix[i], ...matrix[j]])].sort(
(a, b) => a - b
);
matrix[i].length = 0;
flag = true;
break;
}
}
}
}
}
}
return matrix.filter((arr) => arr.length);
}
// 判断两个端口组是否可合并
function canMerge(m, n) {
m = [...m].sort((a, b) => a - b);
n = [...n].sort((a, b) => a - b);
let i = 0;
let j = 0;
let count = 0;
while (i < m.length && j < n.length && count < 2) {
if (m[i] === n[j]) {
i++;
j++;
count++;
} else if (m[i] > n[j]) {
j++;
} else {
i++;
}
}
return count >= 2;
}