＜论文阅读＞FLIRT：二维激光数据的兴趣区域及其在机器人导航中的应用

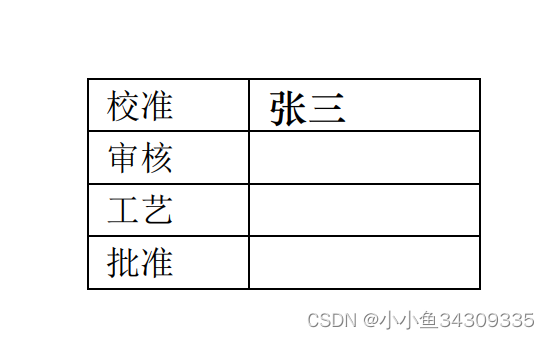
摘要：在这篇文章中，我们提出了FLIRT（快速激光兴趣区域变换），用于 2D 激光数据的多尺度兴趣区域算子。FLIRT结合了基于大地线（是指地球椭球面上两点间的最短程曲线）的曲线近似范围信号的探测器和基于占用概率极坐标直方图的描述符。在标准室内和室外数据集的一组比较基准实验中发现了这种组合，该分析与计算机视觉文献中针对兴趣点发现的值重复性和匹配性能相似，鼓励FLIRT在二维激光数据上的广泛应用。我们展示了FLIRT与RANSAC的结合，如何通过特别简单的算法应用于闭环、全局定位、增量建图和基于位姿估计的SLAM。结果表明，FLIRT特征在精确召回性能、效率、通用性和简单性方面对机器人导航具有巨大潜力。

1 Introduction

局部图像特征的引入对许多计算机视觉任务产生了巨大影响，如物体和场景识别、运动跟踪、立体匹配或视觉机器人定位和SLAM。典型的策略是在图像空间中选择感兴趣的位置，并计算区域上的独特描述符，以这些位置为中心。这将图像内容描述为可用于匹配的局部感兴趣区域的集合。对于稳定位置的检测和编码图像结构的描述，都有多种方法可用于图像距离数据。上述领域产生兴趣点的原因也适用于机器人中广泛使用的激光扫描仪产生的2D距离数据。
在这里插入图片描述

对于机器人导航，兴趣点有可能成为基于特征和基于网格的方法的替代方案，虽然这两种方式在类似应用的条件下都被证明是成功的，它们都有优缺点。几何特征允许紧凑的地图表示和高精度，但依赖于预定义的模型。从这个意义上讲，使用原始数据或网格的密集方法是通用的，但随着地图大小和维度的变化，其缩放效果较差。另一方面，兴趣点结合了离散特征的紧凑性和原始距离数据的通用性。

Mikolajczyk 等人对图像的不同检测器和描述符进行了比较，对于三维数据，已经提出了几种方法来将比例空间从图像扩展到三维点云，用连通性模型表示的表面代替常规图像网格。Taubin 的一项开创性工作，通过扩散方程的离散对应物取代了连续拉普拉斯算子，Pauly等人提出了一种不同的拉普拉斯图 $_g$ 方法，计算了表面变化量。该量由在采样点的局部邻域中计算的样本协方差矩阵的特征值形成，Novatnack 和 Nishino 使用表面几何表示检测多尺度特征，该表达由嵌入在规则密集2D域中的曲面法线编码。然而，该方法依赖于连接网格来构造参数化，并依赖于良好曲面法线的可用性。Unnikrishnan 等人定义了一个将输入曲线映射为多尺度参数化的积分算子。该算子在大地线的坐标中沿着曲线定义，兴趣点在大地线的邻域中被发现为局部极值。利用激光测距仪的数据，Cole 等人提出了局部显著性的信息论测量方法，以在测量空间中找到自然特征。然而，对于穷举搜索，显著性计算是昂贵的，并且作者只计算随机选取的点的显著性值。

对于二维距离数据，几乎没有相关工作。与本文最接近的是 Bosse 和 Zlot 的工作路线。其中，作者将整个激光扫描定义为特征，并使用方向直方图来描述它们。另一个，针对基于子地图的SLAM应用程序中的位置识别任务，评估了2D距离数据的几对检测器/描述符。虽然有趣，但与我们的方法的主要区别是，在子地图上定义了9×9m的描述符支持区域，这些子地图是20-30次扫描的集合，间隔为1−相距2米，他们的方法是子地图特征化技术，而不是局部兴趣点算子。虽然这一特性并不限制于论文中给出的良好结果，但我们有兴趣为2D范围数据设计一个通用的多尺度关键点，该关键点保留了局部性的重要概念，而局部性是视觉兴趣点成功的关键。FLIRT功能就是本着这种精神设计的：它们是在局部定义的（在典型地0.5米半径的支持区域）和在单帧扫描上。

2D距离数据不同于图像数据和3D点云的原因是多方面的。作为一种简单的方法，可以将计算机视觉技术应用于距离数据，用距离信号代替图像强度值。虽然这种方法得到了一些结果，但它无法处理许多兴趣的结构，因为这些结构周围的范围变化可能很弱（角落就是一个例子）。这是因为距离数据的性质不同于图像数据的性质，因为距离数据表示更高维度空间中的流形。在3D范围数据的情况下，该流形是3D中的曲面，对于2D数据，它是笛卡尔空间中的曲线。此外，对于距离数据，测量稀疏度是高度不均匀的，并且视点变化，部分原因是测距仪的角度分辨率比相机低，这些差异激发了2D范围数据特殊衍生的兴趣点变换。本文扩展了我们之前的工作，其中我们比较了2D距离数据的几种检测器和描述符方法，并提出FLIRT是稳定性和匹配性能方面最强大的组合。在这里，我们报告了FLIRT应用于导航问题的综合实验，如全球定位、环路闭合、增量建图和SLAM。

本文的结构如下。第2节介绍了FLIRT探测器和描述符。第3节描述了FLIRT如何应用于机器人导航，第4节给出了实验结果。第5节总结了本文。

2 FLIRT

在本节中，我们介绍了快速激光兴趣点变换（FLIRT），这是一种用于二维距离数据的多尺度兴趣点算子。该算子由基于距离信号的大地线曲线近似的检测器和基于占用概率的极性直方图的描述符组成。这种特殊的组合是综合评估的结果，我们在一组基准实验中比较了四个不同的检测器和两个描述符。现在我们将描述FLIRT检测器和描述符。

2.1基于曲率的检测器

探测器来源于 Unnikrishnan 和 Hebert 针对3D点云的方法，应用于2D距离数据。该检测器背后的基本原理是距离数据定义笛卡尔空间中的曲线，尺度空间理论应应用于该曲线而不是原始信号。
在这里插入图片描述
应用于该曲线而不是原始信号。作者定义了一个将输入曲线映射到多尺度参数化的积分算子。
$\int_Γk(s,u;t)a(u)du \tag{1}$ $\mathcal{N}(s-u;t) \tag{2}$
其中 $Γ$ 是曲线，$α(s)是大地线的坐标s的参数化， $k (s, u; t)$ 是高斯核,然后，通过用（未知）采样密度 $p (s; t)$ 归一化平滑核，
$\tilde{k}(s,u;t) = {k(s,u;t)\over p(s;t)p(u;t)} \tag{3}$ $p(s;t)=\int k(s,u;t)p(u)du \tag{4}$
尺度 $t$ 处的采样密度$p(s;t)，通过使用高斯核的局部核密度估计来近似。这产生了每个刻度的曲线，
$\tilde{S}(a(s);t)=\int_{Γ}{\tilde k(s,u;t)a(u)du} \tag{5}$
增加 $t$ 的平滑度。然后通过找到指数阻尼表达式的局部最大值来检测兴趣点
${2||x-\tilde S(a(s);t)|| \over t} e^{2||x-\tilde S(a(s);t)| \over t|} \tag{6}$
$||x-\tilde S(a(s);t)||$ 是原始曲线与其平滑版本 $\tilde S(a(s);t)$ 之间在笛卡尔空间中的误差距离。利用该方法， $t$ 尺度下的兴趣点对应于 $t$ 等于平滑信号的局部曲率的倒数的位置 $\tilde S(a(s);t)$ 。示例检测结果如图2和图4所示。

2.2β-网格描述符

图像和距离数据之间的一个重要区别是，距离数据编码度量距离，但也编码传感器（发出光或声音）和测量对象之间的定向自由空间信息。占用网格自然地处理自由空间信息，这就是为什么我们采用这个概念来为二维范围数据构建有意义的描述符。具体来说，对于每个检测到的兴趣点 $p_{det}$ ，我们定义了围绕 $p_{det}$ 的空间的极轴细分。这种细分在极轴空间中是线性的，其半径与兴趣点的比例成比例。为了估计占用概率，我们应用贝叶斯参数学习。这种方法提供了一种可靠的方法来初始化小区概率，并对占用值进行方差估计。

我们现在导出了占用网格的贝叶斯参数估计表达式。考虑第 $j$ 个格子，其被光束 $b$ 击中的可能性遵循伯努利分布，由格子占用概率 $occ_j$ 参数化，其中当激光束在格子内反射（击中）时， $b$ 等于 $1$ ，当激光束穿过格子（未击中）时 $b$ 等于 $0$ 。占用概率使用伯努利的共轭先验进行建模，伯努利是贝塔分布，这是一个在区间[0，1]上定义的连续分布，由两个正形状参数 $α$ 和 $β$ 进行参数化，
$p_β(occ_j;α,β) = {occ_j^{a-1}(1-occ_j)^{β-1} \over B(α,β)} \tag{7}$
其中 $B (α, β)$ 是 $E u l e r β$ 函数。得到占用概率 $occ_j$ 包括估计 $B e t a$ 分布的参数（因此描述符的名称）。注意，兴趣点还定义了一个由曲率给出的方向。该方向用于获得旋转不变量。
在这里插入图片描述
在一系列测量中，也就是说，一系列光束 ${b_i}^n_{i＝1}$ ，击中或者未击中箱子，更新规则如下:
$α_i = α_{i-1} + \sum 1^{b_i}$ $β_i = β_{i-1} +\sum1^{1-b_i} \tag{8}$
对于 $i = 0$ ，两个参数都设置为 $1$ ，其 $B e t a$ 分布在 $[0 ， 1]$ 上是均匀的。点估计值为后验贝塔分布的期望值:
$\hat{occ_j} = {α\over {α+β}} = {hit +1 \over hit + misses +2} \tag{9}$
因此，该概率的方差为:
$var(occ_j) = {αβ \over {α+β}^2(α+β+1)} \tag{10}$
极坐标直方图中占用概率的集合及其方差估计构成了 $p_det$ 的 $b e t a$ 网格描述符
在这里插入图片描述