数学建模常用算法之Logistic回归
- 目录
- 一元回归
- 一元线性回归
- 一元非线性回归
- 多元回归
- 逐步回归
- logistic回归
目录
一元回归
一元线性回归
最小二乘法
设:
y=bx+a
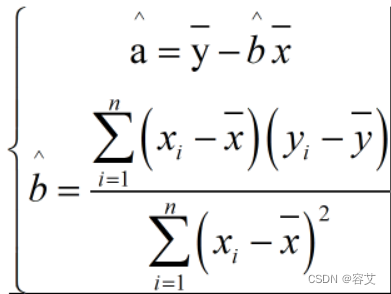
即可求得
%% 输入数据
clc, clear all, close all
x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];
%% 采用最小二乘回归
% 绘制散点图,判断是否具有线性关系
figure
plot(x,y,'r*') %作散点图
xlabel('x(职工工资总额)','fontsize', 12) %横坐标名
ylabel('y(商品零售总额)', 'fontsize',12) %纵坐标名
set(gca,'linewidth',2);
% 采用最小二乘拟合
Lxx=sum((x-mean(x)).^2);
Lxy=sum((x-mean(x)).*(y-mean(y)));
b1=Lxy/Lxx;
b0=mean(y)-b1*mean(x);
y1=b1*x+b0;
hold on
plot(x, y1,'linewidth',2);
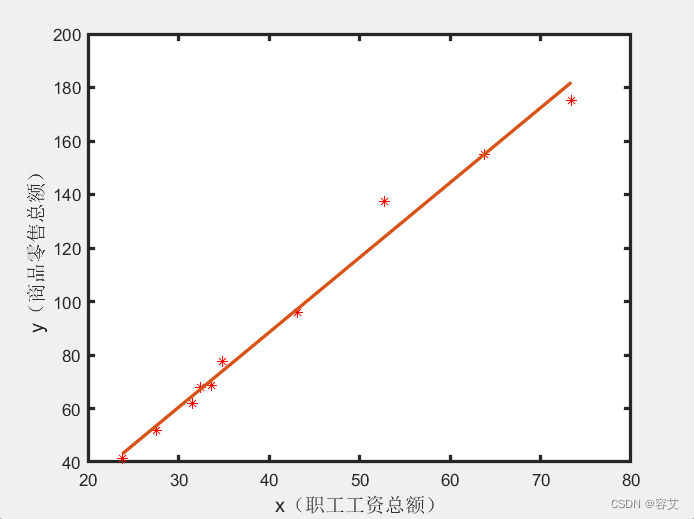
其他方法
- linearModel.fit函数
%% 采用LinearModel.fit函数进行回归
m2 = LinearModel.fit(x,y)
线性回归模型:
y ~ 1 + x1
估计系数:
Estimate SE tStat pValue
________ _______ ______ __________
(Intercept) -23.549 5.1028 -4.615 0.0017215
x1 2.7991 0.11456 24.435 8.4014e-09
观测值数目: 10,误差自由度: 8
均方根误差: 5.65
R 方: 0.987,调整 R 方 0.985
F 统计量(常量模型): 597,p 值 = 8.4e-09
- regress函数
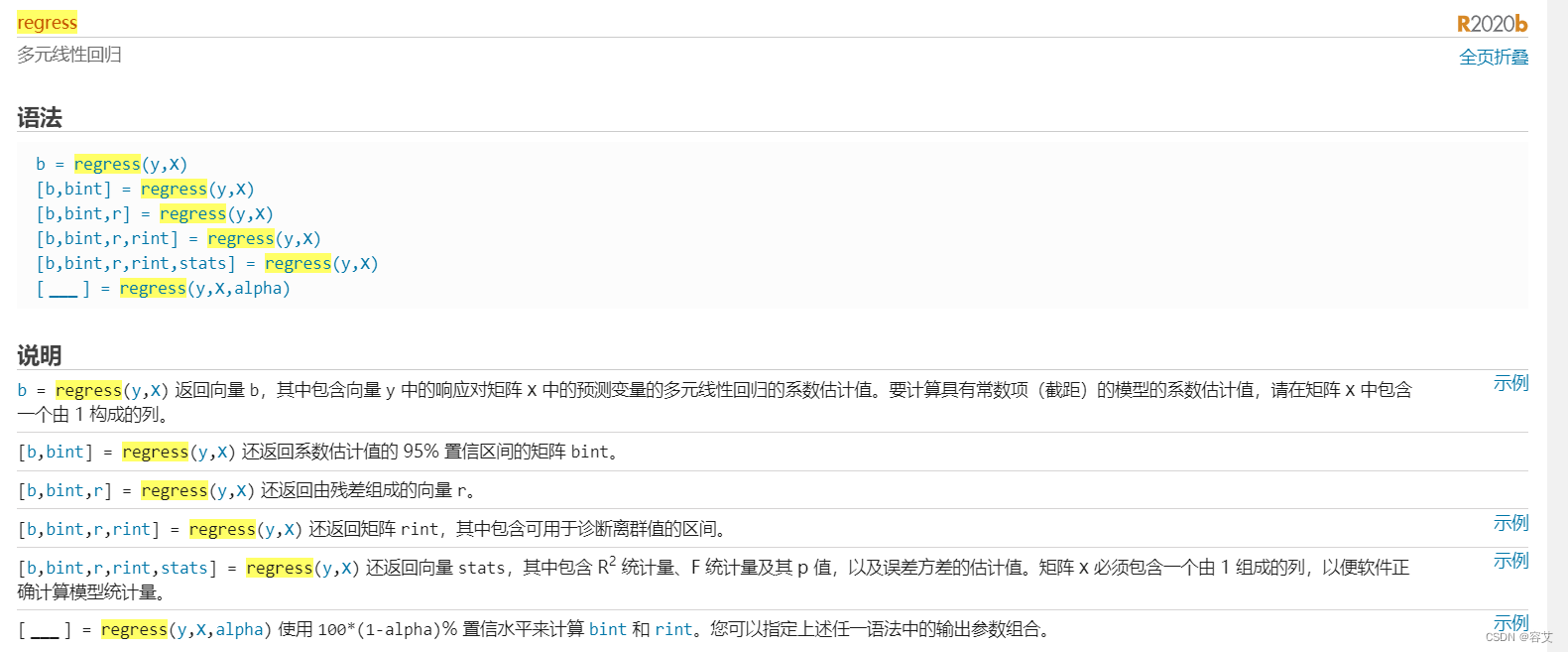
%% 采用regress函数进行回归
Y=y';
X=[ones(size(x,2),1),x'];
[b, bint, r, rint, s] = regress(Y, X)
b =
-23.5493
2.7991
bint =
-35.3165 -11.7822
2.5350 3.0633
r =
-1.6697
-1.9064
-3.2029
0.7578
-2.0810
3.3600
-1.4727
13.1557
-0.0346
-6.9062
rint =
-14.1095 10.7701
-14.7237 10.9109
-16.1305 9.7247
-12.5148 14.0304
-15.3118 11.1497
-9.7162 16.4362
-14.9630 12.0176
7.2091 19.1024
-11.9937 11.9245
-14.7576 0.9453
s =
0.9868 597.0543 0.0000 31.9768
变量解释

一元非线性回归
主要是解决回归方程中的参数估计问题,即fitnlm函数的使用
参考资料:传送门
- 对数形式估计
%% 对数形式
m1 = @(b,x) b(1) + b(2)*log(x);
nonlinfit1 = fitnlm(x,y,m1,[0.01;0.01])
b=nonlinfit1.Coefficients.Estimate;
Y1=b(1,1)+b(2,1)*log(x);
- 指数形式估计
%% 指数形式拟合
m2 = 'y ~ b1*x^b2';
nonlinfit2 = fitnlm(x,y,m2,[1;1])
b1=nonlinfit2.Coefficients.Estimate(1,1);
b2=nonlinfit2.Coefficients.Estimate(2,1);
Y2=b1*x.^b2;
根据xxx.Coefficients.Estimate得到参数
多元回归
观察是否具有线性关系,使用regress函数
X=[ones(n,1),x1',x2',x3'];
[b, bint, r, rint, s] = regress(Y', X,0.05);
逐步回归
资料:传送门
logistic回归
Logistic回归来做分类问题,我们想要的函数应该是,能接受所有的输入然后预测出类别。例如,在两个类的情况下,上述函数输出0或1。
%% 数据准备
clear all
clc
X0=xlsread('logistic_ex1.xlsx', 'A2:C21'); % 回归数据X值
XE=xlsread('logistic_ex1.xlsx', 'A2:C26'); % 验证与预测数据
Y0=xlsread('logistic_ex1.xlsx', 'D2:D21'); % 回归数据P值
%使用二项分布的模型进行预测
GM = fitglm(X0,Y0,'Distribution','binomial');
Y1=predict(GM,XE);
N1=1:1:size(XE,1);
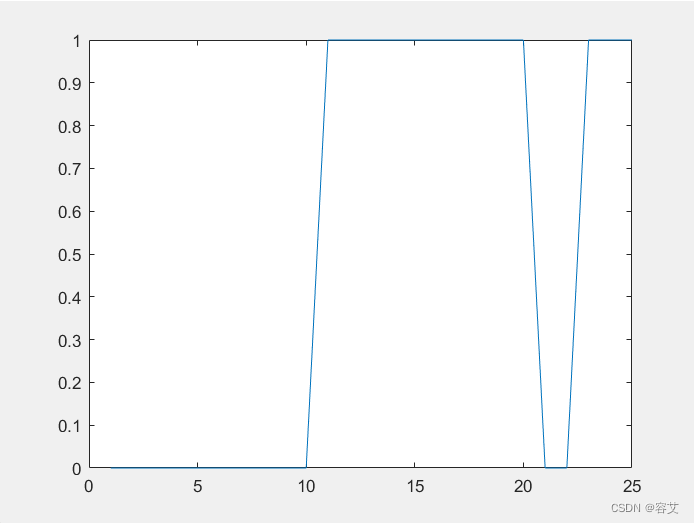
plot(N1',Y1)
结果