文章目录
- 一、474. 一和零
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 二、879. 盈利计划
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 三、377. 组合总和 Ⅳ
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 四、96. 不同的二叉搜索树
- 1.题目简介
- 2.解题思路
- 3.代码
- 4.运行结果
- 总结
二维费用的背包问题:
一、474. 一和零
1.题目简介
474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。

2.解题思路
3.代码
class Solution {
public:
int findMaxForm(vector<string>& strs, int m, int n) {
vector<int> v(m + 1, 0);//初始化
vector<vector<int>> dp(n + 1, v);//dp[j][k]表示满足“最多”有j个1和k个0的strs的最大子集的长度(最多:说明并不一定要求放满,因此不用判断dp[j - v1[i]][k - v0[i]]是否存在)
vector<int> v1(strs.size(), 0);//字符串中1的个数
vector<int> v0(strs.size(), 0);//字符串中0的个数
for(int i = 0;i < strs.size(); ++i)//将字符串中的1和0分别存放
{
for(int j = 0;j < strs[i].size(); ++j)
{
if(strs[i][j] == '1') v1[i]++;
else v0[i]++;
}
}
for(int i = 0;i < strs.size(); ++i)
{
//题意可知这些字符串每个都只能使用一次,属于01背包问题,因此背包的遍历顺序是从后往前
for(int j = n;j >= v1[i]; --j)
{
for(int k = m;k >= v0[i]; --k)
{
dp[j][k] = max(dp[j - v1[i]][k - v0[i]] + 1, dp[j][k]);//放这个字符串和不放
}
}
}
return dp[n][m];//如果凑不出满足需要的子集,则返回0
}
};
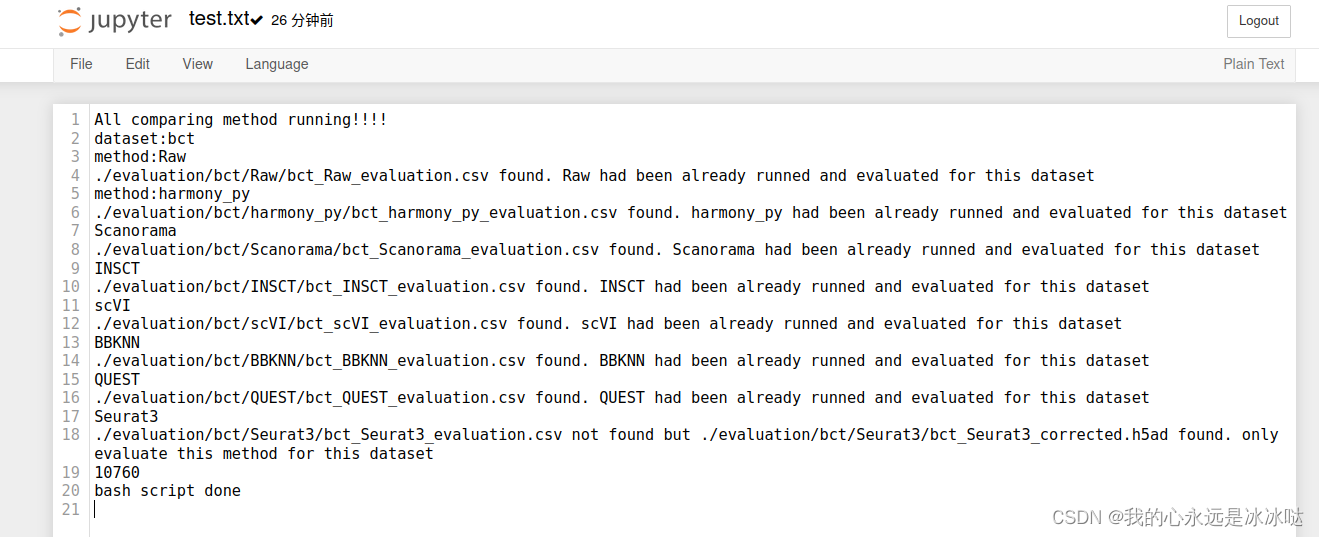
4.运行结果
二、879. 盈利计划
1.题目简介
879. 盈利计划
集团里有 n 名员工,他们可以完成各种各样的工作创造利润。
第 i 种工作会产生 profit[i] 的利润,它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作,就不能参与另一项工作。
工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。
有多少种计划可以选择?因为答案很大,所以返回结果模 10^9 + 7 的值。

2.解题思路
3.代码
class Solution {
public:
int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {
int mod = 1e9 + 7;
//由题意可知,这是一个01背包问题中的二维费用背包问题(二维指的是人数和利润这两个维度)
vector<int> v(minProfit + 1, 0);
vector<vector<int>> dp(n + 1, v);//dp[j][k]表示至少产生k的利润,最多提供j个员工时的计划数
//初始化利润为0时的dp表
for(int j = 0;j <= n; ++j)//无论人数是多少,我们都可以找到一个空集的方案
{
dp[j][0] = 1;
}
for(int i = 0;i < group.size(); ++i)
{
for(int j = n;j >= group[i]; --j)//(人数绝对不能是小于0的,因此j要大于等于group[i])
{
for(int k = minProfit;k >= 0; --k)//利润可以等于0,但是正常情况下利润是不小于0的,因此k - profit要和0取较大值
{
dp[j][k] += dp[j - group[i]][max(0, k - profit[i])];//求计划数(求组合数,用+)
dp[j][k] %= mod;
}
}
}
return dp[n][minProfit];
}
};
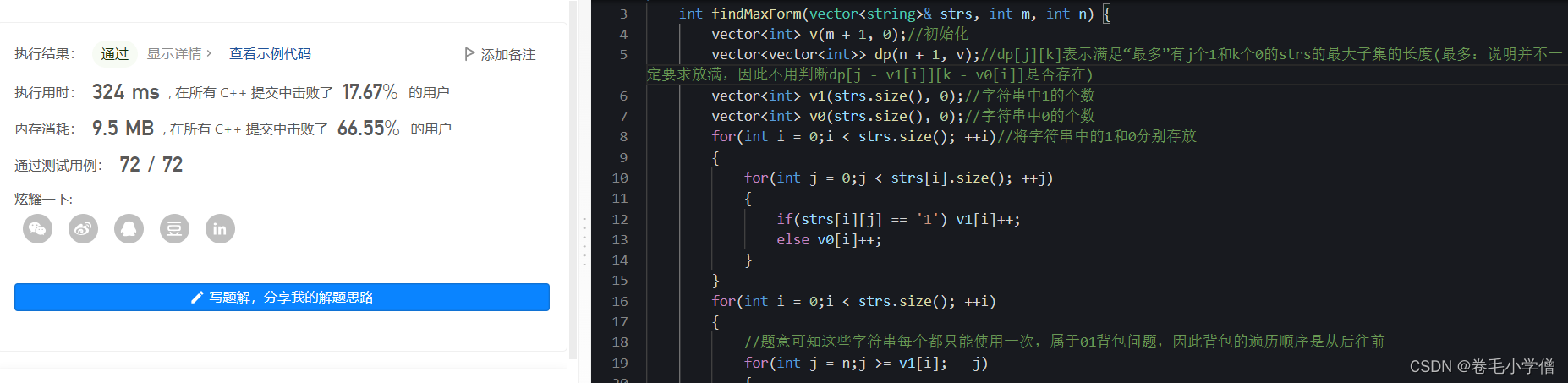
4.运行结果
似包非包的问题:
三、377. 组合总和 Ⅳ
1.题目简介
377. 组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围。


2.解题思路
3.代码
class Solution {
public:
//1.多重背包问题:遍历背包要从左往右
//2.本质是求排列个数的问题:对顺序有要求,则先遍历背包再遍历物品
int combinationSum4(vector<int>& nums, int target) {
vector<int> dp(target + 1, 0);//dp[j]表示凑成总和为j的元素组合个数
dp[0] = 1;
for(int j = 0;j <= target; ++j)
{
for(int i = 0;i < nums.size(); ++i)
{
if(j >= nums[i] && dp[j] < INT_MAX - dp[j - nums[i]])
dp[j] += dp[j - nums[i]]; //计算组合数、排列数用+
}
}
return dp[target];
}
};
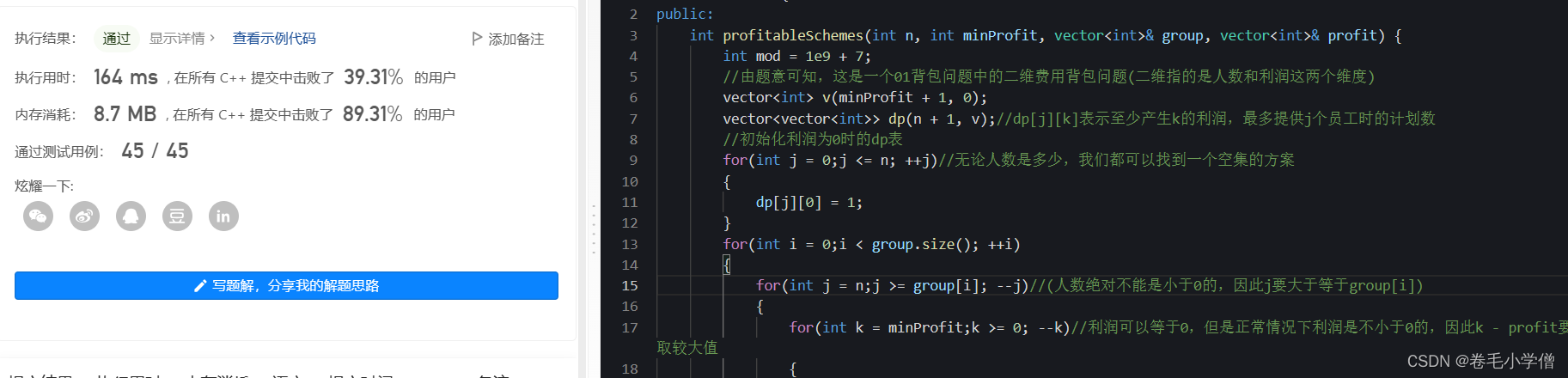
4.运行结果
四、96. 不同的二叉搜索树
1.题目简介
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。

2.解题思路
3.代码
class Solution {
public:
int numTrees(int n) {
if(n == 0 || n == 1) return 1;
if(n == 2) return 2;
vector<int> dp(n + 1, 0);//dp[i]表示当有i个节点时,它所能形成的二叉搜索树的种数
dp[0] = 1;//空树
dp[1] = 1;//只有一个根节点
dp[2] = 2;
for(int i = 3;i <= n; ++i)
{
int left = i - 1, right = 0;//left是左子树的节点个数,right是右子树的节点个数
while(left >= 0)
{
dp[i] += dp[left--] * dp[right++];
}
}
return dp[n];
}
};
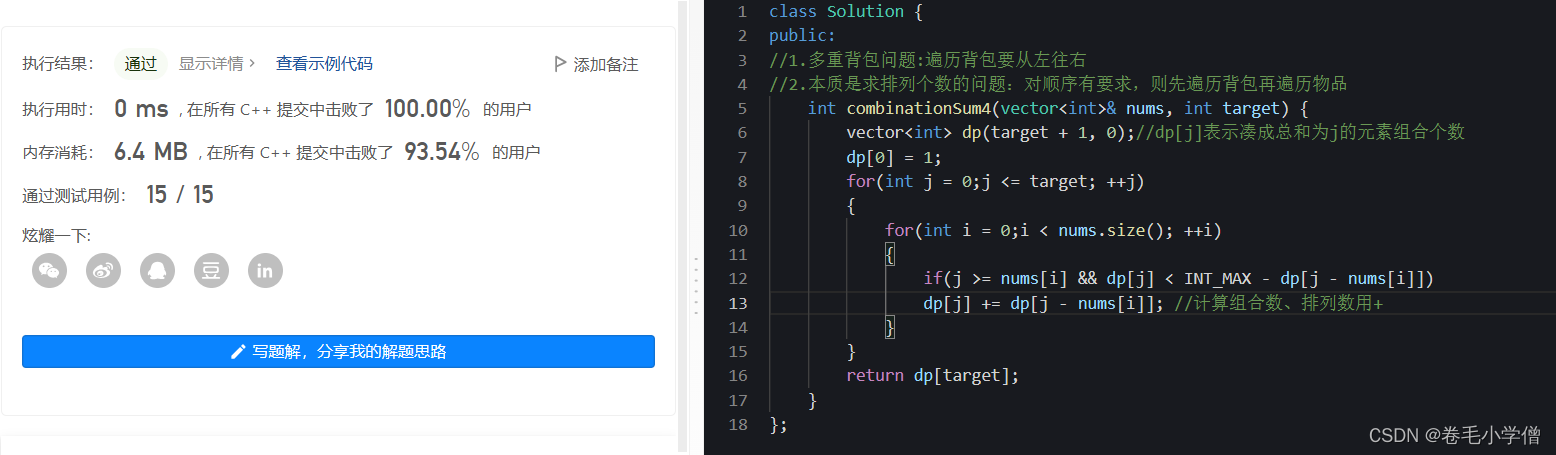
4.运行结果
总结
今天是算法练习的第17天。
及时当勉励,岁月不待人 ,动态规划算法练习到此告一段落。
来源:力扣(LeetCode),著作权归领扣网络所有。
如果本篇文章对你有所启发的话,希望可以多多支持作者,谢谢大家!