文章目录
- 重叠区间:452. 用最少数量的箭引爆气球
- 解法1——左边界排序
- 解法2——右边界排序
- 无重叠区间:435. 无重叠区间
- 解法1——左边界排序
- 解法2——右边界排序
- 合并区间:56. 合并区间
- 左边界排序
- 这题为什么不能按照右边界排序?
- 其实右边界排序也是可以写的!
本文内容包括 重叠区间、不重叠区间、合并区间 的 左边界排序、右边界排序 方法。
重叠区间:452. 用最少数量的箭引爆气球
452. 用最少数量的箭引爆气球
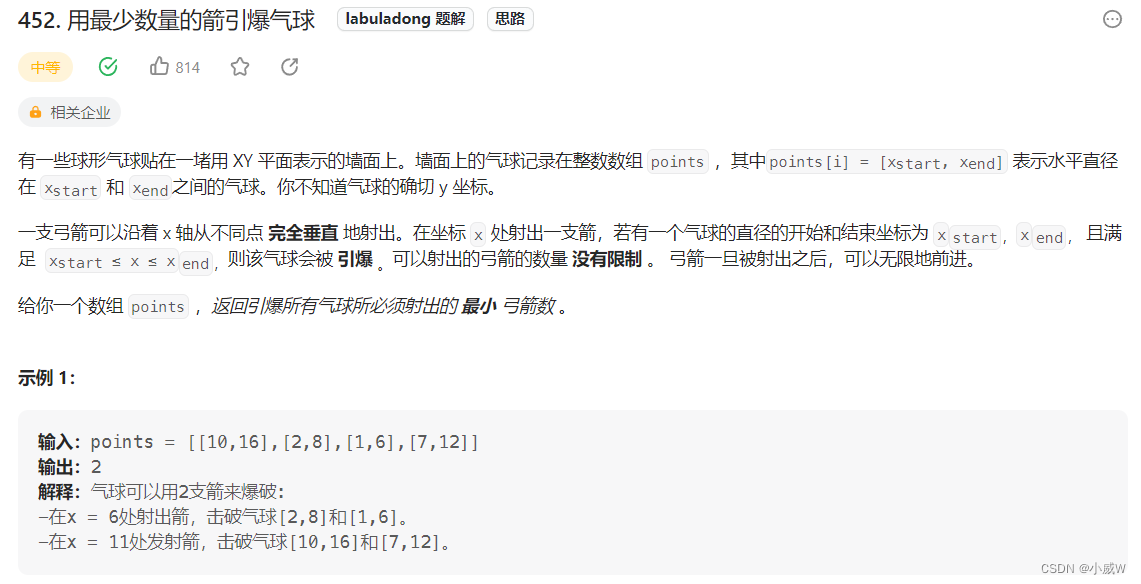
解法1——左边界排序
按照左边界升序排序,在枚举的过程中只需要检查新来的左边界与旧的右边界的关系并更新最小右边界。
class Solution {
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (o1, o2) -> {
return Integer.compare(o1[0], o2[0]); //按左边界排序
});
int ans = 1, n = points.length, last = points[0][1];
for (int i = 1; i < n; ++i) {
if (points[i][0] > last) { // 需要一个新的弓箭
++ans;
last = points[i][1];
} else last = Math.min(last, points[i][1]); // 更新最小右边界
}
return ans;
}
}
解法2——右边界排序
按照右边界排序时,只需比较新来的左边界和当前右边界的关系。(由于是按右边界排序的,因此只有需要新弓箭时才需要更新右边界。)
class Solution {
public int findMinArrowShots(int[][] points) {
Arrays.sort(points, (o1, o2) -> {
return Integer.compare(o1[1], o2[1]);
});
int ans = 1, n = points.length, last = points[0][1];
for (int i = 1; i < n; ++i) {
if (points[i][0] > last) {
++ans;
last = points[i][1];
}
}
return ans;
}
}
无重叠区间:435. 无重叠区间
435. 无重叠区间
解法1——左边界排序
按左边界排序时,每次发现重叠的时候需要更新最小右边界,依次保证每次发生重叠,保留的都是位于左侧的。
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return a[0] - b[0];
});
int ans = 0, last = intervals[0][1];
for (int i = 1; i < intervals.length; ++i) {
if (intervals[i][0] < last) {
++ans;
last = Math.min(intervals[i][1], last);
} else last = intervals[i][1];
}
return ans;
}
}
解法2——右边界排序
按照右边界排序时,只有不重叠时才需要更新右边界。(因为是按右边界排序的,因此每次保留的一定是最靠左的右边界了。)
class Solution {
public int eraseOverlapIntervals(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return Integer.compare(a[1], b[1]);
});
int ans = 0, last = intervals[0][1];
for (int i = 1; i < intervals.length; ++i) {
if (intervals[i][0] < last) ++ans;
else last = intervals[i][1];
}
return ans;
}
}
可以看出这道题和上一题超级像!
合并区间:56. 合并区间
56. 合并区间
左边界排序
class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return a[0] - b[0];
});
List<int[]> ans = new ArrayList();
int last = Integer.MIN_VALUE;
for (int i = 0; i < intervals.length; ++i) {
if (intervals[i][0] > last) {
ans.add(new int[]{intervals[i][0], intervals[i][1]});
last = intervals[i][1];
} else {
last = Math.max(last, intervals[i][1]);
ans.get(ans.size() - 1)[1] = last;
}
}
return ans.toArray(new int[ans.size()][2]);
}
}
这题为什么不能按照右边界排序?
看这样一个样例:[[2,3],[4,5],[6,7],[8,9],[1,10]]
按照右边界排序时,最后一个区间突然可以将之前的所有区间包裹住,但是前面的 4 个区间都各不重叠无法合并。
其实右边界排序也是可以写的!
其实右边界排序也是可以写的,把左边界排序的代码全都反过来操作就可以了!
class Solution {
public int[][] merge(int[][] intervals) {
Arrays.sort(intervals, (a, b) -> {
return a[1] - b[1];
});
List<int[]> ans = new ArrayList();
int last = Integer.MAX_VALUE;
for (int i = intervals.length - 1; i >= 0; --i) {
if (intervals[i][1] < last) {
ans.add(new int[]{intervals[i][0], intervals[i][1]});
last = intervals[i][0];
} else {
last = Math.min(last, intervals[i][0]);
ans.get(ans.size() - 1)[0] = last;
}
}
return ans.toArray(new int[ans.size()][2]);
}
}