1.简述
-
直线检测是数字图像处理的重要内容,在道路识别,建筑物识别,医学图像分析等领域都有十分重要的应用。通过对已经获得的图像进行边缘检测,然后用Hough变换对边缘检测进行直线检测。该方法简单,受直线中的间隙和噪声影响较小。在Matlab环境下对该方法进行了仿真实验,并对图像中直线目标进行了检测,结果表明用该方法对图像中直线目标进行检测是快速有效的。
2.代码
function chengxu()
%% 第1步
close all
I=imread('1.jpg'); %读取图像
I=rgb2gray(I); %彩色图像转换成灰度图
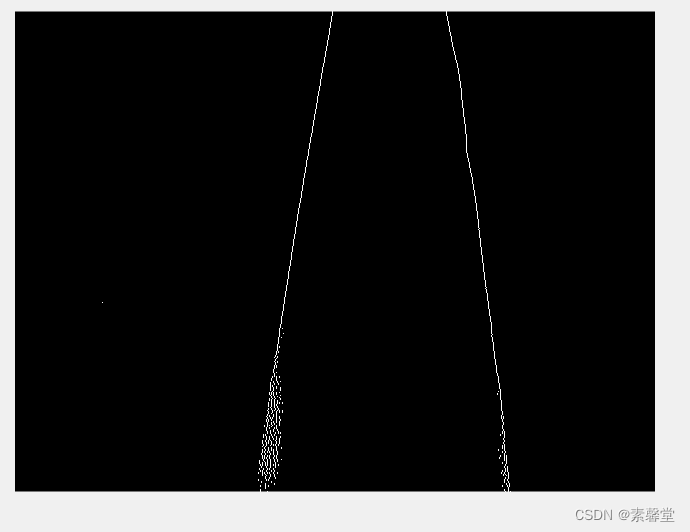
I=edge(double(I)); %检测图像的边缘
figure
imshow(I) %显示边缘检测的结果
%% 第2步
[m,n]=size(I); %计算图像的尺寸
M=3; %定义X方向分割的块数
N=3; %定义Y方向分割的块数
mm=floor(m/M); %子块行的长度
nn=floor(n/N); %子块列的长度
count=1; %计数器
figure
for i=1:M
for j=1:N
A=I((i-1)*mm+1:i*mm,(j-1)*nn+1:j*nn); %分割原图像,得到一个子块
subplot(M,N,count)
imshow(A) %显示一个子块
zuoshangjiao=[(i-1)*mm+1 (j-1)*nn+1]; %子块左上角的坐标
[x,y,k,b]=zikuai(A,zuoshangjiao);%得到子块里白色像素点拟合得到的直线的斜率k和截距b(调用zikuai函数)
X{count}=x; %保存子块里所有白色像素的x坐标
Y{count}=y; %保存子块里所有白色像素的y坐标
K(count)=k; %保存子块里拟合得到的直线的斜率k
B(count)=b; %保存子块里拟合得到的直线的截距b
count=count+1; %计数器加1,进行下一个子块的计算
end
end
%% 第3步
KK=K(~isnan(K)); %去掉K中的NaN(白色像素点少于10的子块)
BB=B(~isnan(B)); %去掉B中的NaN(白色像素点少于10的子块)
mean_K=mean(KK); %求所有斜率的平均值
mean_B=mean(BB); %求所有截距的平均值
figure
subplot(2,1,1)
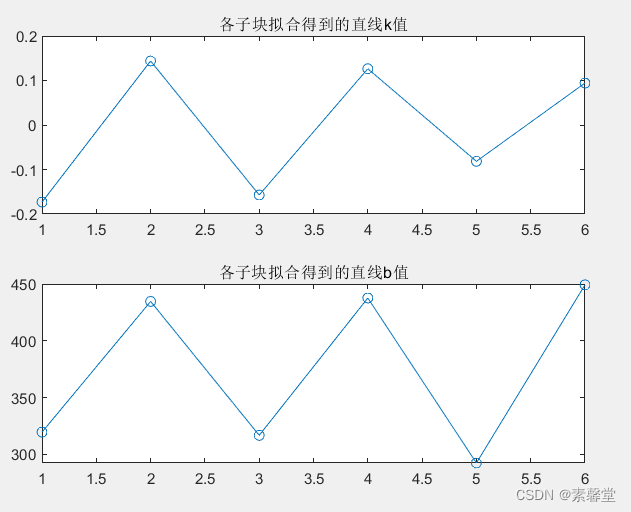
plot(KK,'-o')
title('各子块拟合得到的直线k值')
subplot(2,1,2)
plot(BB,'-o')
title('各子块拟合得到的直线b值')
count1=1;
count2=1;
for i=1:length(K)
if ~isnan(K(i))
if K(i)>mean_K %大于斜率平均值的子块,将这些子块的白色像素点位置集合到cell型数组X1和Y1(分别存x和y)
X1{count1}=X{i};
Y1{count1}=Y{i};
count1=count1+1;
else %小于斜率平均值的子块,将这些子块的白色像素点位置集合到cell型数组X2和Y2(分别存x和y)
X2{count2}=X{i};
Y2{count2}=Y{i};
count2=count2+1;
end
end
end
XX1=[];
YY1=[];
XX2=[];
YY2=[];
for i=1:length(X1) %大于斜率平均值的子块,将这些子块的白色像素点位置集合到double型数组里,方便计算
XX1=[XX1;X1{i}];
YY1=[YY1;Y1{i}];
end
for i=1:length(X2) %小于斜率平均值的子块,将这些子块的白色像素点位置集合到double型数组里,方便计算
XX2=[XX2;X2{i}];
YY2=[YY2;Y2{i}];
end
%% 直线1和直线2被从图像里提取出来了分别为XX1,YY1和XX2,YY2
%% 离散点拟合得到直线1的斜率k1和截距b1
A1=[XX1,ones(length(XX1),1)];
kb1=A1\YY1;
k1=kb1(1);
b1=kb1(2);
%% 离散点拟合得到直线2的斜率k2和截距b2
A2=[XX2,ones(length(XX2),1)];
kb2=A2\YY2;
k2=kb2(1);
b2=kb2(2);
xx0=[1 m];
yy0=[1 n];
yy1=k1*xx0+b1; %得到直线1上的两点,以便绘制直线1
yy2=k2*xx0+b2; %得到直线3上的两点,以便绘制直线2
%% 绘制拟合得到的直线和分离出来的离散点
%% 直线1
figure
axis([1,m,1,n]) %设定显示范围
hold on
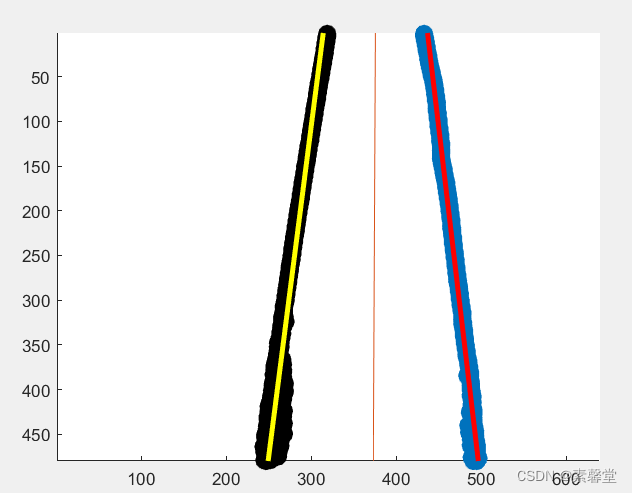
scatter(XX1,YY1,'LineWidth',5) %绘制直线1对应的白色像素位置
plot(xx0,yy1,'r','LineWidth',3) %绘制拟合到的直线1
%% 直线2
hold on
scatter(XX2,YY2,'k','LineWidth',5) %绘制直线2对应的白色像素位置
plot(xx0,yy2,'y','LineWidth',3) %绘制拟合到的直线2
%% 第4步
%% 求两条直线的交点
X0=(b2-b1)/(k1-k2);
Y0=k1*X0+b1;
alpha=atan(k1); %直线1与x夹角
beta=atan(k2); %直线2与x夹角
K01=tan((alpha+beta)/2); %角平分线1的斜率
K02=tan(-pi/2+(alpha+beta)/2); %角平分线2的斜率
B01=Y0-K01*X0; %角平分线1的截距
B02=Y0-K02*X0; %角平分线2的截距
%% 绘制角平分线
xx0=[1 m];
yy0=[1 n];
YY1=K01*xx0+B01; %角平分线1
YY2=K02*xx0+B02; %角平分线2
plot(xx0,YY1); %绘制角平分线1
plot(xx0,YY2); %绘制角平分线2
view([90 90])
end
function [x,y,k,b]=zikuai(feikuai,zuoshangjiao)
%% 求每个子块数据拟合出来的直线y=kx+b,返回k和b,以及子块里白色像素点的坐标
x0=zuoshangjiao(1); %得到子块的左上角x坐标
y0=zuoshangjiao(2); %得到子块的左上角y坐标
[m,n]=size(feikuai); %计算子块的大小
N=1; %N从1开始计数
x=[]; %定义子块白色像素x坐标保存的向量x
y=[]; %定义子块白色像素y坐标保存的向量y
for i=1:m %依次扫描子块各个点的像素值
for j=1:n
if feikuai(i,j)==1 %如果是白色像素,保存该像素的坐标
x(N)=i; %保存相对坐标(x方向)
y(N)=j; %保存相对坐标(y方向)
N=N+1; %计数加1,判断下一个像素
end
end
end
if length(x)<10 %少于10个白色像素的子块(包括没有白点的子块),舍弃掉(点数太少,可能是噪声)
k=NaN; %将k b x y 赋值NaN(Matlab系统变量,表示Not a Number),以示与其他子块的区别
b=NaN;
x=NaN;
y=NaN;
return %返回
else %子块白色像素点个数大于等于10,对白色像素点的坐标进行拟合,得到直线的斜率k和截距b
x=x+x0; %得到子块内白色像素点相对于原图像的绝对坐标x
y=y+y0; %得到子块内白色像素点相对于原图像的绝对坐标y
x=x';
A=[x,ones(length(x),1)]; %定义矩阵A(直线拟合就是解超越线性方程组的最小二乘解,未知数为k和b)即A*[k;b]=y';
y=y';
kb=A\y; %得到最小二乘解,对应k和b
k=kb(1); %得到k
b=kb(2); %得到b
end
end
3.运行结果