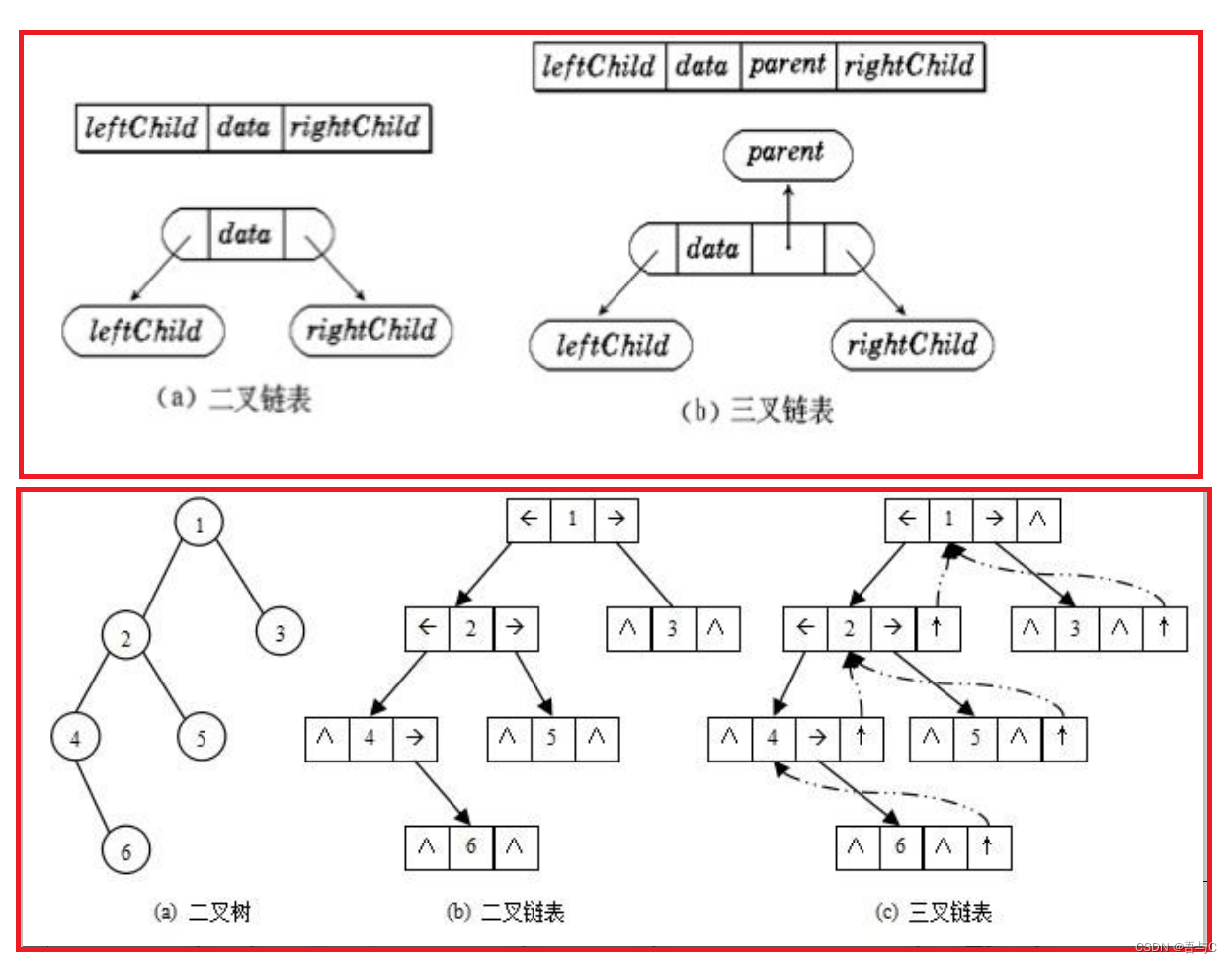
数据结构–二叉树的先中后序遍历
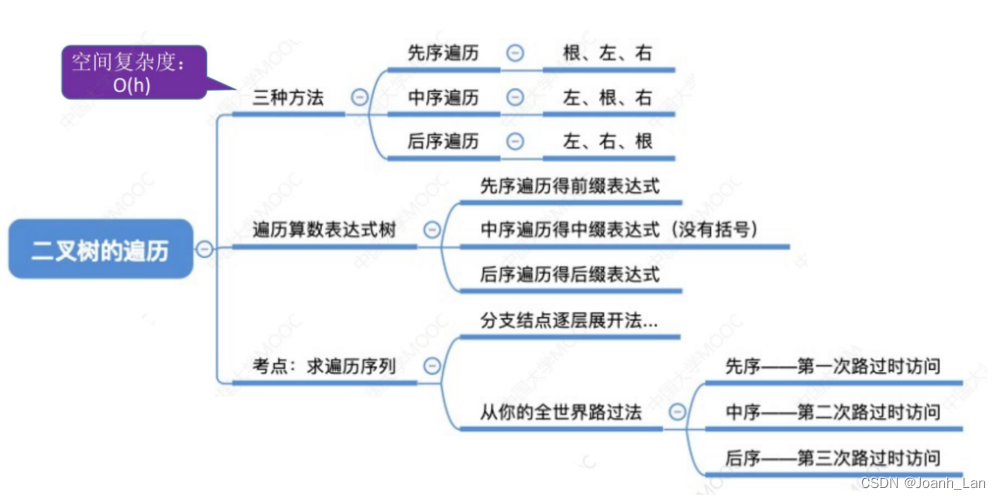
二叉树的遍历
层次遍历
层次遍历:基于树的层次特性确定的次序规则
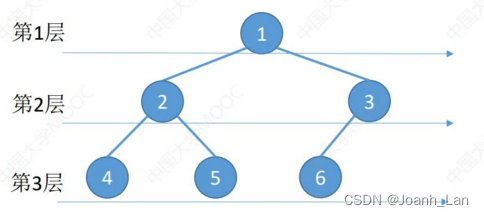
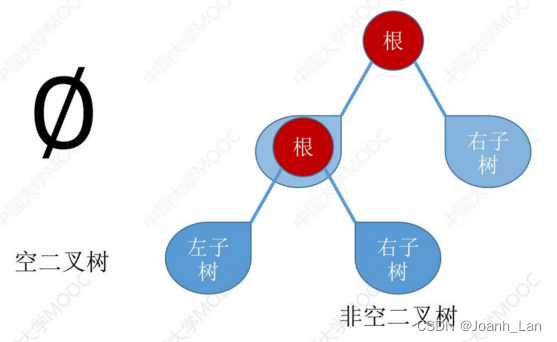
二叉树的递归特性:
①要么是个空二叉树
②要么就是由“根节点+左子树+右子树”组成的二叉树
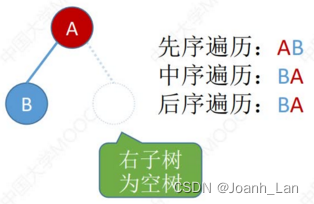
先
\color{red}先
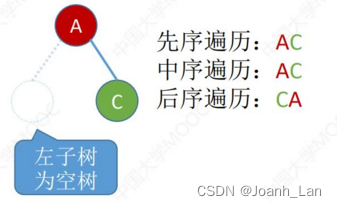
先序遍历:
根
\color{red}根
根左右(
N
\color{red}N
NLR)
中
\color{red}中
中序遍历:左
根
\color{red}根
根右(L
N
\color{red}N
NR)
后
\color{red}后
后序遍历:左右
根
\color{red}根
根(LR
N
\color{red}N
N)


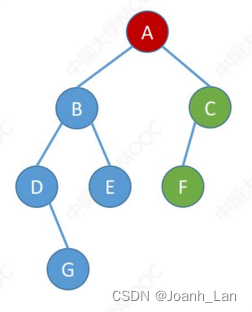
序遍历:
A B D G E C F
中序遍历:
D G B E A F C
后序遍历:
G D E B F C A
算数表达式的“分析树”
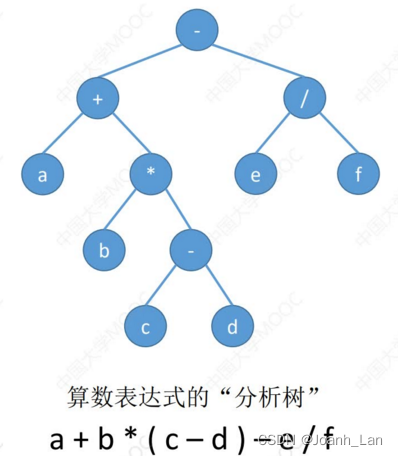
先序遍历: -+ab-cd/ ef
中序遍历: a+bc-d-e/f
后序遍历: abcd-*+ef/-
先序遍历→前缀表达式
中序遍历→中缀表达式(需要加界限符)
后序遍历→后缀表达式
先序遍历代码
先序遍历
\color{red}先序遍历
先序遍历(PreOrder)的操作过程如下:
1.若二叉树为空,则什么也不做;
2.若二叉树非空:
①访问根结点;
②先序遍历左子树;
③先序遍历右子树。
\color{red}③先序遍历右子树。
③先序遍历右子树。
void PreOrder(BiTree T)
{
if (T != NULL)
{
visit(T); //访问根结点
PreOrder(T->lchild); //递归遍历左子树
PreOrder(T->rchild); //递归遍历右子树
}
}
中序遍历代码
]
中序遍历
]\color{red}中序遍历
]中序遍历(InOrder)的操作过程如下:
1.若二叉树为空,则什么也不做;
2.若二叉树非空:
①中序遍历左子树;
②访问根结点
;
\color{red}②访问根结点;
②访问根结点;
③中序遍历右子树。
void InOrder(BiTree T)
{
if (T != NULL)
{
InOrder(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrder(T->rchild); //递归遍历右子树
}
}
后序遍历代码
后序遍历
\color{red}后序遍历
后序遍历 ( PostOrder)的操作过程如下:
1.若二叉树为空,则什么也不做;
2.若二叉树非空:
①后序遍历左子树;
②后序遍历右子树;
③访问根结点。
\color{red}③访问根结点。
③访问根结点。
void PostOrder(BiTree T)
{
if (T != NULL)
{
PostOrder(T->lchild); //递归遍历左子树
PostOrder(T->rchild); //递归遍历右子树
visit(T); //访问根结点
}
}
求树的深度(应用)
int treeDepth(BiTree T)
{
if (T == NULL) return 0;
int l = treeDepth(T->lchild);
int r = treeDepth(T->rchild);
//树的深度=Max(左子树深度,右子树深度)+1
return l > r ? l + 1 : r + 1;
}
知识点回顾与重要考点