专题：数组

题目：有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

示例 2： 输入：nums = [-7,-3,2,3,11] 输出：[4,9,9,49,121]

 题目分析：

方法一暴力循环：最简单的想法，遍历一次数组，同时给数组的每个元素*=自己。但是同时发现，如果这样做，那么原来比较小的负数，平方之后。变成了比较大的数字。不符合 非递减顺序 排序。但是可以利用sort()排序函数，对它排序。但是代码的效率不够高。

代码实现：

 

 方法二双指针法：申请一个新的和原数组大小一样的数组result。然后left 指向老数组的第一个位置，right指向老数组的最后一个有效元素的位置。然后大的while循环条件是 left<=right;

在这个循环基础下，我们让left指向元素的平方 和 right指向的元素的平方 作比较，left指向元素平方大的话。就将这个值放到新数组的最后一个位置。然后left++。再次进行比较...如果right对应元素的平方大的话，就将right对应的元素的平方放入新数组，并且right--.直到最后left 大于  right 不满足条件，退出循环。此时就将旧数组的，所有元素的平方，按照非递减的顺序排在新数组中。

细节注意： 对于数组的大小，边界，nums.size() 以及 nums.size()-1的把握；

nums.size():表示的是数组的元素个数（因为元素个数按照1,2,3,4.....nums.size() ）

nums.size()-1:表示的是数组有效元素下标(因为元素下标按照0,1,2,3,4.....nums.size()-1)

要充分理解，上面一一对应的关系。

申请一个和原来数组大小一样的数组：vector<int> result(nums.size(),0);

如果访问新数组中的最后一个元素：  result[nums.size() -1];

代码实现：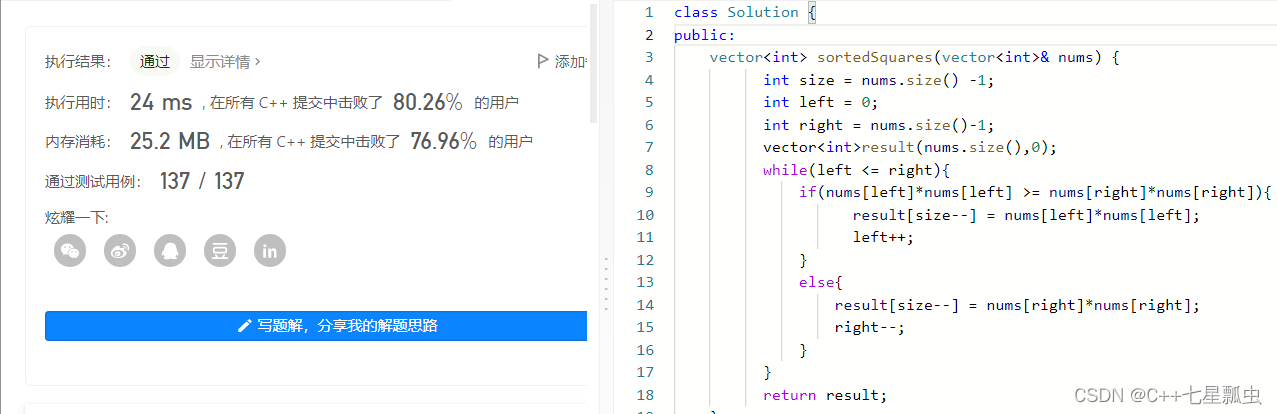 

题目：长度最小子数组 

给定一个含有 n 个正整数的数组和一个正整数 s ，找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组，并返回其长度。如果不存在符合条件的子数组，返回 0。

示例：

输入：s = 7, nums = [2,3,1,2,4,3] 输出：2 解释：子数组 [4,3] 是该条件下的长度最小的子数组。

题目分析

方法一暴力法：两个for循环。大循环每到一个元素，小循环就从这个元素开始往后累加，直到当前这个值大于等于 目标值，此时记录此时的小数组长度（即小循环和大循环的下标差+1） 判断此时的小数组长度 和 最终的小数组长度result比较，如果此时的小数组长度小于最终小数组长度 那么更新 最终小数组长度 ，否则最终的小数组长度不变。然后小循环接结束break，大循环走到下一个元素。继续....直到结束！ 但是这样会超时！！！

细节注意： 长度统计时注意: j - i +1;

                   对于break的使用，一旦这个小循环里面找到了最短的长度，就可以直接退出这                次的小循环了。直接break;

                   ？表达式的使用；

代码实现

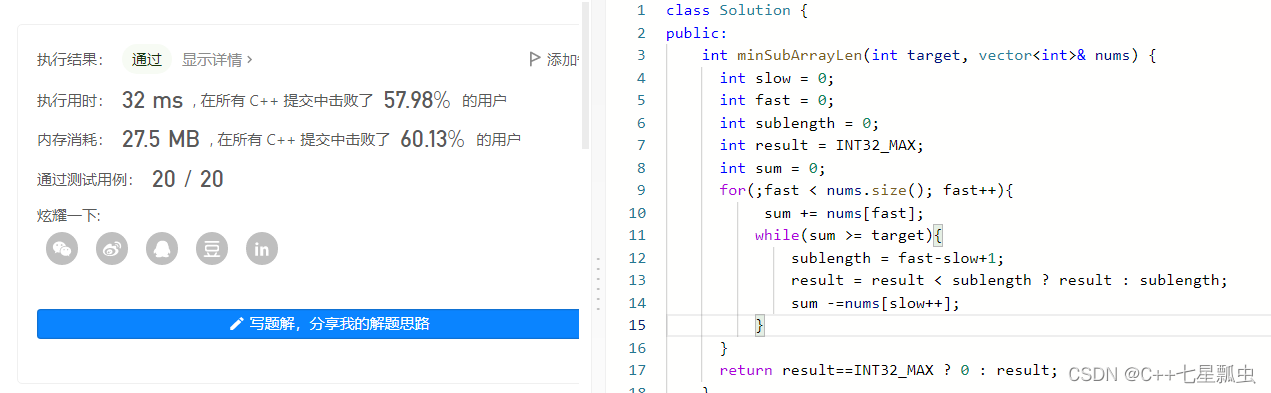
方法二滑动窗口法：两个下标fast和slow，使用fast进行for循环，并且进行fast对于元素的累加。直到当前累加的值，大于目标值。然后记录当下子数组的长度（fast - slow +1），然后让当前的累加值 减去 slow下标对于的元素的值，然后slow下标++。继续执行循环。

细节注意：核心原理就是 sum - nums[slow++];  

                  注意判断条件是while；（很重要！！！）

代码实现: 

 题目 螺旋矩阵

给定一个正整数 n，生成一个包含 1 到 n^2 所有元素，且元素按顺时针顺序螺旋排列的正方形矩阵。

示例:输入: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ]

题目分析

 模拟顺时针画矩阵的过程:

• 填充上行从左到右
• 填充右列从上到下
• 填充下行从右到左
• 填充左列从下到上

细节注意

 为了有规律每次都是，每一行都是，第一个到倒数第二个。这样的话，就可以用一个规律，处理所有的行。一定要调整语句，让他可以通过循环完成。需要设置变量的话，就要使用。

代码实现

 

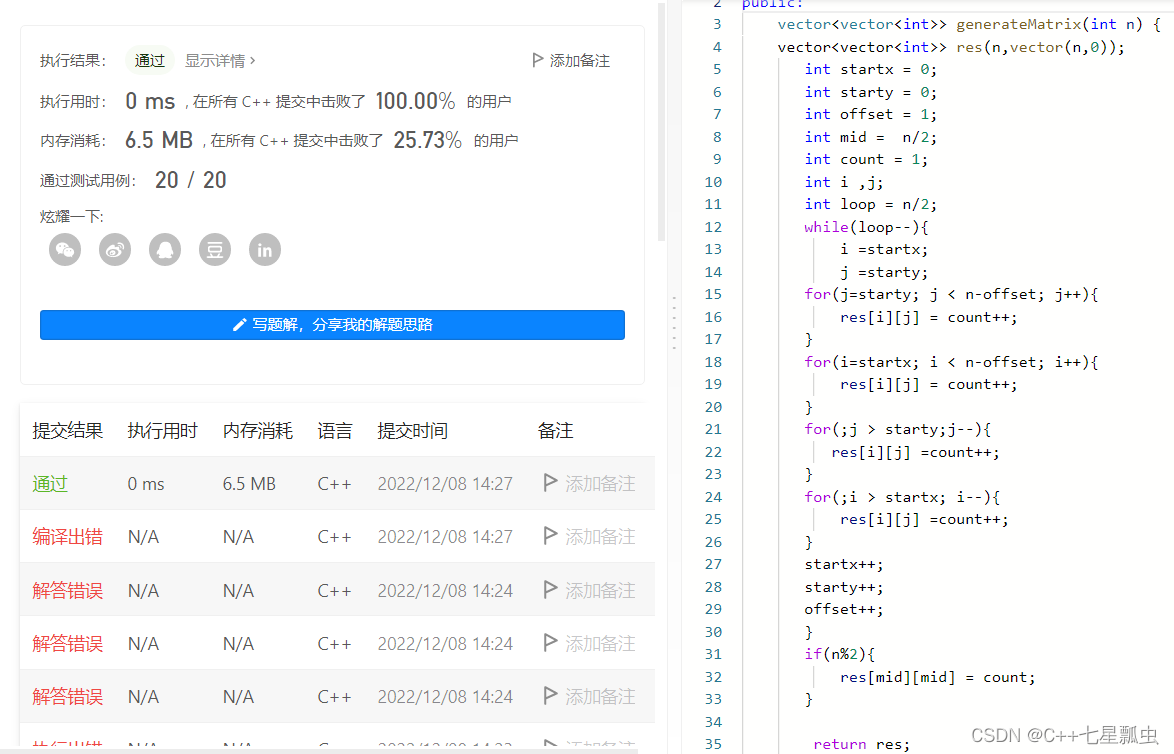
 思考：做题的步奏：

 1.先想明白，做这个题目的思路。（具体步奏，细节处理都是关键）

 2.一旦有了想法，就去动手实现。多使用，多尝试。在题目中真正体验代码的使用。（应用）

 3.标准还是，按照自己的理解，能一次写出来！！！