1、前期准备
(1) 有数据的MongoDB数据库old_db、空数据库new_db
(2) 准备好MongoDB Tools
前往页面:https://www.mongodb.com/try/download/database-tools
选择所需版本下载并解压到自己想要的目录中:
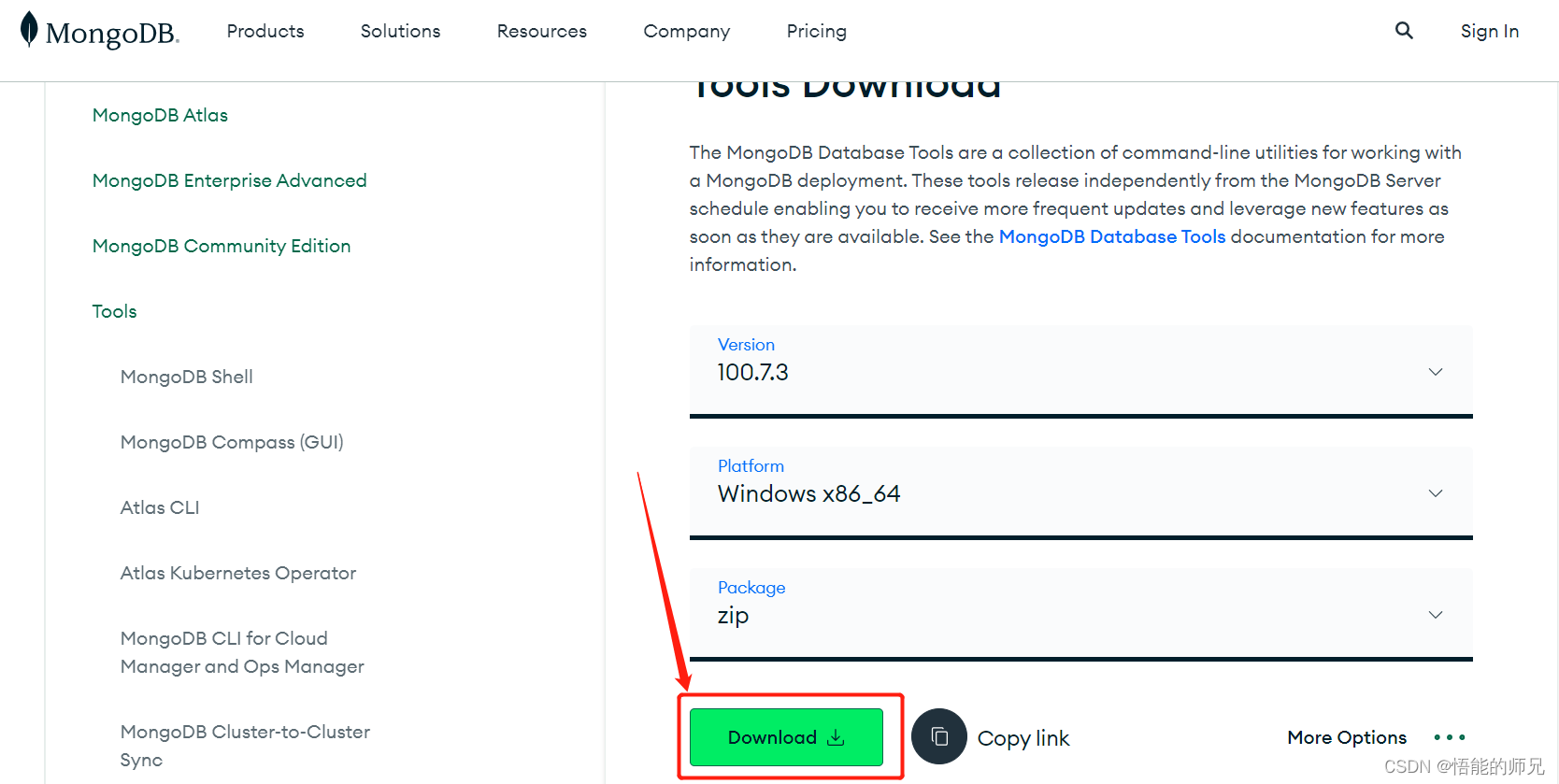
2、将数据库old_db中的数据备份导出
(1) 对old_db右键,选择MongoDump

(2) 找到MongoDump.exe(从Mongo Tools中解压出来的:mongodump.exe)
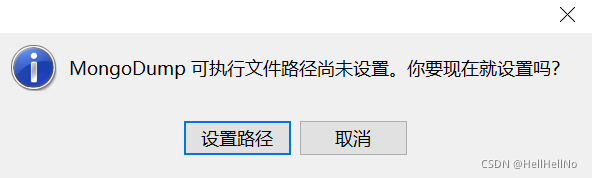
(3) 选择自己想要存放数据的路径(假设为F:\mongoDB_backup),以gz格式存放。压缩后文件大小会只有:10%的样子。
3、将来自old_db的集合test_data导入到new_db
(1) 对new_db右键,选择MongoRestore
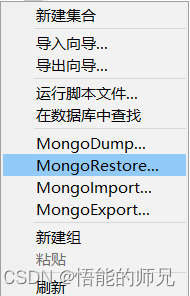
(2) 选择以gz格式,在F:\mongoDB_backup中取出test_data.gz导入
部分参考:Navicat导入、导出MongoDB的集合