1. 二叉排序树（中序遍历是有序的）

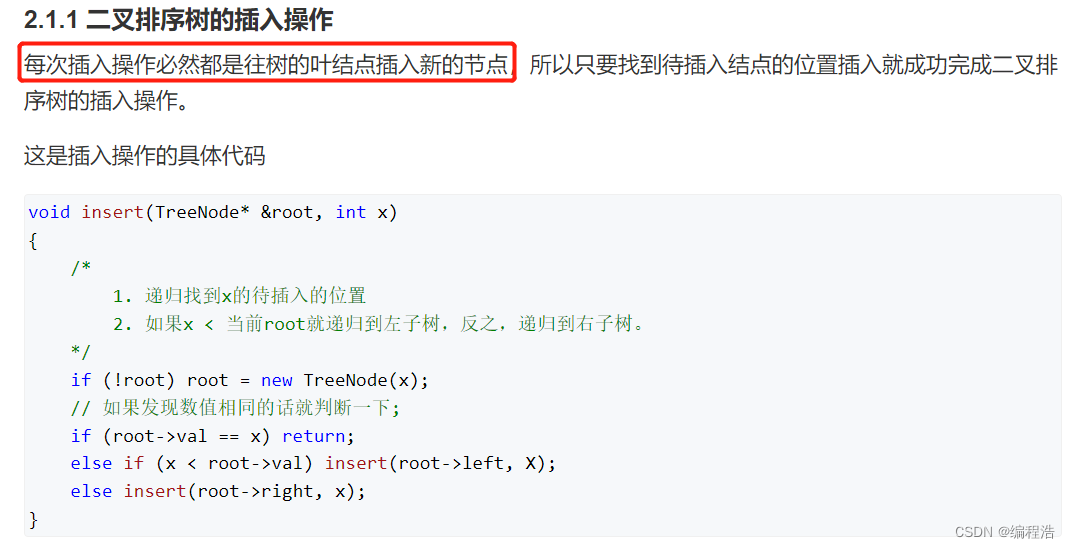
解释一下删除操作的第三点：

首先我们要清楚：
二叉排序树的特点是
中序遍历（左根右）是有序的

所以如果删除的根节点有左右子树

那么我们为了保证有序

就要把 根节点左子树的最右边 赋值给根节点
因为根节点左子树的最右边是比根节点小中最大的点

只有这样才能保证删除根节点后

左子树比新的根节点都小
右子树比新的根节点都大

#include <bits/stdc++.h>

using namespace std;

const int INF = 2e9;

struct TreeNode
{
    int val;
    TreeNode *left, *right;
    TreeNode(int _val): val(_val), left(NULL), right(NULL) {}
}*root;

// 插入操作
void insert(TreeNode* &root, int x)
{
    /*
        1. 递归找到x的待插入的位置
        2. 如果x < 当前root就递归到左子树，反之，递归到右子树。
    */ 
    if (!root) root = new TreeNode(x);
    // 如果发现数值相同的话就判断一下;
    if (root->val == x) return;
    else if (x < root->val) insert(root->left, x);
    else insert(root->right, x);
}

void remove(TreeNode* &root, int x)
{
    /*
        1. 待删除的结点只有左子树。立即可推出，左子树上的结点都是小于待删除的结点的，我们只需要把待删除结点删了然后左子树接上待删除结点的父节点就可以了。
        2. 待删除的结点只有右子树。立即可推出，右子树上的结点都是大于待删除的结点的，我们只需要把待删除结点删了然后右子树接上待删除结点的父节点就可以了。
        3. 待删除的结点既有左子树又有右子树。这个比上两个情况麻烦一点，但也不麻烦，需要读者理解的是，怎么能删除结点后还不改变中序遍历的结果，并且操作代价最小，显而易见，我们根据待删除结点的左子树可以得到最右下角的最后结点满足$<x$并且最接近x的结点，把这个结点覆盖待删除的结点，然后把这个结点删除，就完成了我们的操作。
    */

    // 如果不存在直接return
    if (!root) return;
    if (x < root->val) remove(root->left, x);
    else if (x > root->val) remove(root->right, x);
    else
    {
        if (!root->left && !root->right) root = NULL;
        else if (!root->left) root = root->right;
        else if (!root->right) root = root->left;
        else
        {
            auto p = root->left;
            while (p->right) p = p->right;
            root->val = p->val;
            remove(root->left, p->val);
        }
    }
}

// 输出数值 x 的前驱(前驱定义为现有所有数中小于 x 的最大的数)。
int get_pre(TreeNode* root, int x)
{
    if (!root) return -INF;
    if (root->val >= x) return get_pre(root->left, x);
    else return max(root->val, get_pre(root->right, x));
}

// 输出数值 x 的后继(后继定义为现有所有数中大于 x 的最小的数)。
int get_suc(TreeNode* root, int x)
{
    if (!root) return INF;
    if (root->val <= x) return get_suc(root->right, x);
    else return min(root->val, get_suc(root->left, x));
}

int main()
{
    int n;
    cin >> n;
    while (n--)
    {
        int t, x;
        cin >> t >> x;
        if (t == 1) insert(root, x);
        else if (t == 2) remove(root, x);
        else if (t == 3) cout << get_pre(root, x) << endl;
        else cout << get_suc(root, x) << endl;
    }
    return 0;
}