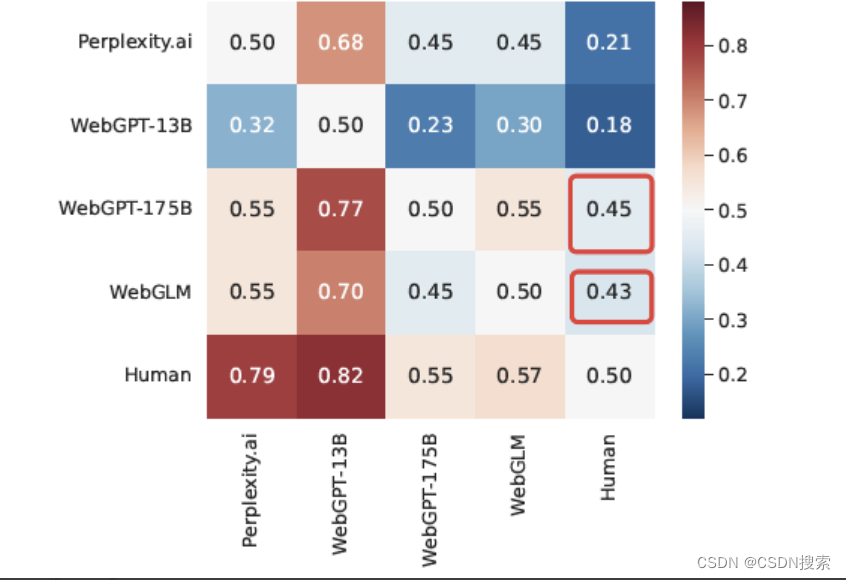
相机模型存在4个坐标系：世界坐标系、摄像机坐标系、图像物理坐标系和图像像素坐标系。

光心：图像的中心。
光轴：穿过图像的光心，与图像平面垂直的轴。

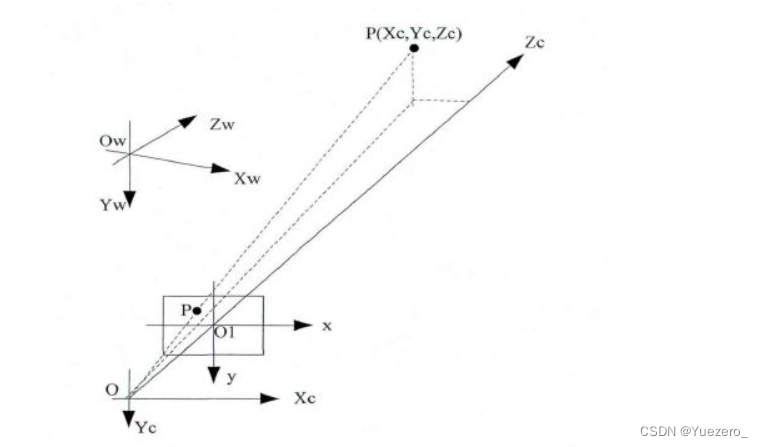
• 世界坐标系(Xw,Yw,Zw)：是客观三维世界的绝对坐标系，也称客观坐标系，就是物体在真实世界中的坐标，世界坐标系是随着物体的大小和位置变化的，单位是长度单位
• 相机坐标系(Xc,Yc,Zc)：以相机的光心为坐标原点，以平行于图像的x和y方向为x轴和y轴，z轴和光轴平行，x， y，z互相垂直，单位是长度单位。
• 图像物理坐标系(X,Y)：以主光轴Zc和图像平面交点为坐标原点，x’和y’方向如图所示，单位是长度单位。
• 图像像素坐标系(Xc,Yc)：以图像的上/下/左/右顶点为坐标原点，u和v方向平行于x’和y’方向，单位是像素。(图像物理坐标系和像素坐标系仅通过平移可重合)

为什么空间坐标系之间的线性变换关系 = 坐标轴向量堆叠？

从线性代数的角度来解释，三个轴向量按列排列形成一个3x3的矩阵，这个矩阵可以表示空间坐标系之间的线性变换关系。在这种情况下，这个矩阵可以表示从世界坐标系到相机坐标系的转换。

在三维空间中，我们通常使用右手坐标系来描述物体的位置和方向。对于一个相机坐标系来说，它的三个轴向量（通常是单位向量）分别表示相机的右、上和前方向。

考虑一个点P在世界坐标系中的表示为列向量[Px, Py, Pz]，通过乘以转换矩阵R可以将其转换到相机坐标系中的表示为列向量[Cx, Cy, Cz]，即：

[Cx, Cy, Cz] = R * [Px, Py, Pz]

其中，R是一个3x3的矩阵，表示从世界坐标系到相机坐标系的转换。矩阵R的每一列分别对应相机坐标系的三个轴向量。

通过矩阵乘法运算，可以将世界坐标系中的点P转换到相机坐标系中的点C。这个过程实质上是对点P进行了旋转和平移操作，使得点P相对于相机坐标系的原点发生了变化。

因此，将三个轴向量按列排列形成一个3x3的矩阵，可以方便地表示空间坐标系之间的线性变换关系，从而实现将世界坐标系中的点转换到相机坐标系中的点。