向量点乘dot
点乘是向量的一种运算规则,点乘也有其它称呼,比如点积、数量积、标量积。
threejs三维向量Vector3封装了一个点乘相关的方法.dot(),本节课主要目的就是让大家能够灵活应用点乘方法.dot()
已知向量a和向量b
已知两个向量a和b,默认夹角是45度。
const a = new THREE.Vector3(10, 10, 0);
const b = new THREE.Vector3(20, 0, 0);向量点乘.dot()语法
下面先给大家说下点乘.dot()的语法,然后再讲解它的用途。 a.dot(b)表示向量a与向量b点乘,返回结果是一个数字(标量)
//向量a与向量b点乘,返回结果是一个数字
const dot = a.dot(b);
console.log('点乘结果',dot);点乘.dot()几何含义
你只需要记住a.dot(b)的几何含义是向量a在向量b上投影长度与向量b相乘,或者说向量a长度 * 向量b长度 * cos(ab夹角)。
const a = new THREE.Vector3(10, 10, 0);
const b = new THREE.Vector3(20, 0, 0);
// dot几何含义:向量a长度 * 向量b长度 * cos(ab夹角)
const dot = a.dot(b);
console.log('点乘结果',dot);//判断结果是不是200单位向量点乘含义(计算向量夹角余弦值)
假设两个向量的夹角是θ,两个向量的单位向量进行点乘.dot(),返回的结果就是夹角θ的余弦值cos(θ)
const a = new THREE.Vector3(10, 10, 0);
const b = new THREE.Vector3(20, 0, 0);
// a、b向量归一化后点乘
const cos = a.normalize().dot(b.normalize());
console.log('向量夹角余弦值',cos);夹角余弦值转角度值
//反余弦计算向量夹角弧度
const rad = Math.acos(cos);
// 弧度转角度
const angle = THREE.MathUtils.radToDeg(rad);
console.log('向量夹角角度值',angle); // 45点乘判断物体在人前或人后
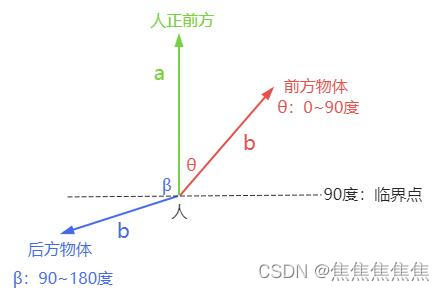
通过three.js向量Vector3点乘方法.dot()判断物体在人的前面还是后面。
已知条件
人的正前方沿着z轴负半轴方向
// a向量:人的正前方沿着z轴负半轴
const a = new THREE.Vector3(0,0,-1);
人的位置和物体的位置
person.position.set(0,0,2);//人位置
mesh.position.set(2,0,-3);//物体位置创建一个人指向物体的向量
物体坐标减去人坐标,创建一个人指向物体的向量
const b = mesh.position.clone().sub(person.position);向量夹角与人前后关系判断
// a向量:人的正前方
const a = new THREE.Vector3(0,0,-1);
// 人指向物体的向量
const b = mesh.position.clone().sub(person.position);