本文为MATLAB基础篇（上）的后续。

---

 二、 MATLAB基本语法

7、基本绘图方法

Ⅰ、 MATLAB绘图的一般步骤

1. 对数轴进行采样
2. 对采样点计算相应的函数值, 得到平面(或空间)上的点的数据
3. 运用绘图命令将数据进行图形化显示

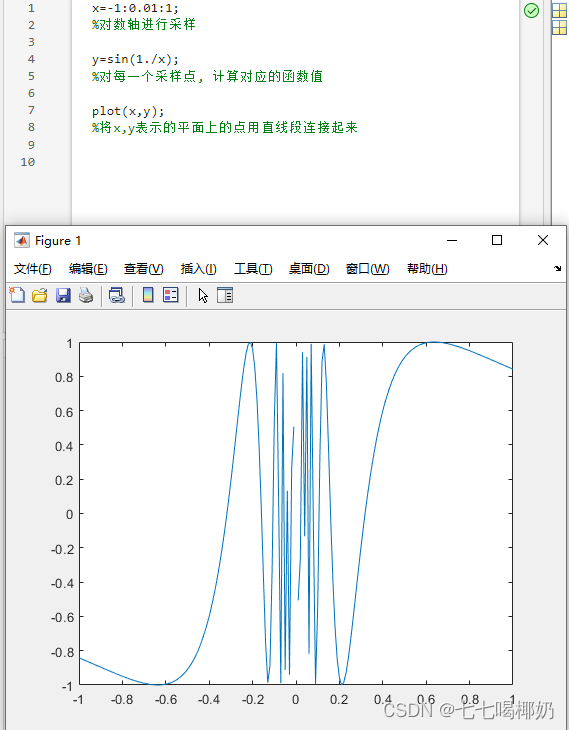
x=-1:0.01:1;
%对数轴进行采样

y=sin(1./x);
%对每一个采样点, 计算对应的函数值

plot(x,y);
%将x,y表示的平面上的点用直线段连接起来

画出y=sin(1/x), x∈[-1,1]的图形，如下：

 Ⅱ、线型、点型和颜色

使用格式: plot(x,y,'绘图参数')

plot(x,y,'*b');  %点型为*,  颜色为蓝色
plot(x,y,':g');  %线型为虚线, 颜色为绿色
plot(x,y,'+-r');  %点型为+,线型为实线, 颜色为红色

                                                                     MATLAB绘图参数表

线型	说明	点型号	说明	颜色	说明
-	实线(默认)	+	加号符	r	红色
--	双划线	o	空心圆	g	绿色
:	虚线	*	星号	b	蓝色
:.	点划线	.	实心圆	c	青绿色
		x	叉号符	m	洋红色
		s	正方形	y	黄色
		d	菱形	k	黑色
		^	上三角形	w	白色
		v	下三角形
		>	右三角形
		<	左三角形
		p	五角星
		h	六边形

 Ⅲ、多条曲线的绘制

有多种方法在一张图上显示多条曲线, 这里介绍两种方法

(1)用plot(x1,y1,x2,y2,…)命令

t=0:0.5:4*pi;
y=exp(-0.1*t).*sin(t);
y1=exp(-0.1*t).*sin(t+1);
plot(t,y,t,y1);

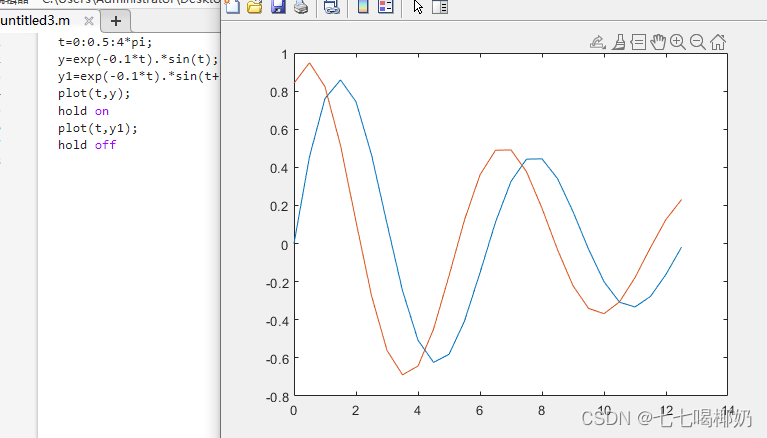
 (2)用hold on命令

在执行一次绘图命令合, 使用hold on命令保持当前画板, 使得后面绘制的图形在当前画板上.

t=0:0.5:4*pi;
y=exp(-0.1*t).*sin(t);
y1=exp(-0.1*t).*sin(t+1);
plot(t,y);
hold on
plot(t,y1);
hold off

 Ⅳ、三维曲线和曲面

（1）绘制三维曲线

格式: plot3(x,y,z)

z=0:0.1:4*pi;
x=cos(z);
y=sin(z);
plot3(x,y,z);

 (2) 绘制三维曲面

步骤:

1. 分别对x,y轴进行采样;
2. 生成x-y平面网格;
3. 计算网格点对应的z值;
4. 用三维曲面绘图命令绘图

x=-8:0.5:8;
y=-8:0.5:8;
[X,Y] = meshgrid(x,y);
R = sqrt(X.^2+Y.^2)+eps;            
Z = sin(R)./R;
mesh(X,Y,Z);

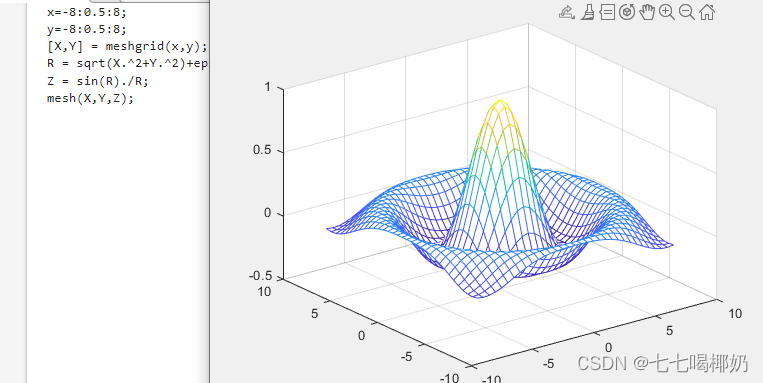
注：在上述公式中，eps是一个非常小的数，通常被称为“机器精度”（machine epsilon）。它用于避免在计算机程序中出现除以零的错误 

                                               常用绘图命令

plot	线性X-Y坐标绘图	legend	标注图例
axis	控制坐标轴比例和外观	plot3	三维曲线作图
hold on	保持当前画板	meshgrid	生成网格
hold off	释放当前画板	mesh	三维曲面作图
title	标题	surf	三维曲面作图
xlabel	X轴标注	meshc	加等高线的三维曲面作图
ylabel	Y轴标注	surfc	加等高线的三维曲面作图
textt	在图上标文字	contour	平面等高线
grid on	图上加坐标网格	contour3	三维等高线
grid off	去掉网格	subplot	子图

8、逻辑运算

MATLAB的逻辑值有真(TRUE)和假(FALSE), 可以通过逻辑表达式或直接输入得到. 输入和显示时用0表示逻辑假, 1表示逻辑真. 浮点数和逻辑值可以互相转换.

                                                    浮点数与逻辑值的相互转换

                           

                                                      关系运算及逻辑运算符

 

符号	意义	符号	意义	符号	意义
>	大于	<	小于	>=	大于或等于
<=	小于或等于	==	等于	~=	不等于
&	逻辑与	|	逻辑或	~	逻辑非
&&	逻辑与(短路)	||	逻辑或(短路)	xor	逻辑异或

A=[0 0 1 1]
B=[0 1 0 1]

A&B                 与                              
A|B                 或
~A                  非
xor(A, B)         异或
G=magic(6)        魔方矩阵
rem(G,2)          G的元素整除2的余数
p=(rem(G, 3)==0)     判断元素是否是0
u=p|~p            两个逻辑数组对应元素进行运算

得到：
A =

     0     0     1     1


B =

     0     1     0     1


ans =

  1×4 logical 数组

   0   0   0   1


ans =

  1×4 logical 数组

   0   1   1   1


ans =

  1×4 logical 数组

   1   1   0   0


ans =

  1×4 logical 数组

   0   1   1   0


G =

    35     1     6    26    19    24
     3    32     7    21    23    25
    31     9     2    22    27    20
     8    28    33    17    10    15
    30     5    34    12    14    16
     4    36    29    13    18    11


ans =

     1     1     0     0     1     0
     1     0     1     1     1     1
     1     1     0     0     1     0
     0     0     1     1     0     1
     0     1     0     0     0     0
     0     0     1     1     0     1


p =

  6×6 logical 数组

   0   0   1   0   0   1
   1   0   0   1   0   0
   0   1   0   0   1   0
   0   0   1   0   0   1
   1   0   0   1   0   0
   0   1   0   0   1   0


u =

  6×6 logical 数组

   1   1   1   1   1   1
   1   1   1   1   1   1
   1   1   1   1   1   1
   1   1   1   1   1   1
   1   1   1   1   1   1
   1   1   1   1   1   1

 魔方阵是一个矩阵，其中每行、每列以及对角线上的所有元素之和都相等。请注意，魔方阵只能在方阵（即行数等于列数）中生成。在生成魔方阵时，算法会优化使得每行、每列和对角线之和都相等。这使得生成的魔方阵在数学和游戏等领域具有一些特殊的性质和用途。

A = rand(4,4)
B = A<0.5
C = A(B)
R = find(A<0.5)
得到：
A =

    0.7094    0.6551    0.9597    0.7513
    0.7547    0.1626    0.3404    0.2551
    0.2760    0.1190    0.5853    0.5060
    0.6797    0.4984    0.2238    0.6991


B =

  4×4 logical 数组

   0   0   0   0
   0   1   1   1
   1   1   0   0
   0   1   1   0


C =

    0.2760
    0.1626
    0.1190
    0.4984
    0.3404
    0.2238
    0.2551


R =

     3
     6
     7
     8
    10
    12
    14

9、流程控制语句

（1）if语句

格式一：

if (表达式)

语句组A;

end

格式二:

if (表达式1)

    语句组A;

else

    语句组B;

end

格式三:

if (表达式1)

    语句组A;

elseif (表达式2)

    语句组B;

else   

    语句组C;

end

(2) while语句

格式:

while  (表达式)

  语句组;

end

举例：求MATLAB相对精度，y不断减小，直至MATLAB分不出1+y与1的差别为止。

y=1;
while (1+y)>1
    y1=y;
    y=y/2;
end
y1 
得到：
y1 =

   2.2204e-16

(3) for语句

格式:

for k= 初值:增量:终值

    语句组;

end

举例：显示三角函数表

for x=0:0.1:pi/4
    disp([x, sin(x), cos(x), tan(x)])
end
得到：
 0     0     1     0

    0.1000    0.0998    0.9950    0.1003

    0.2000    0.1987    0.9801    0.2027

    0.3000    0.2955    0.9553    0.3093

    0.4000    0.3894    0.9211    0.4228

    0.5000    0.4794    0.8776    0.5463

    0.6000    0.5646    0.8253    0.6841

    0.7000    0.6442    0.7648    0.8423

10、M程序及M函数

• MATLAB的程序通常用后缀名为m的文本文件来保存, 所以 可以用任何文字编辑工具来创建和编写.  MATLAB程序可直接调用M文件并执行.
• M文件分为两种: 一种是M程序, 为用户解决特定的问题编制的, 可以独立执行；另一种是M函数, 用来完成相对独立的子功能, 不能独立执行.  MATLAB软件的大部分功能是来自其建立的函数集.
• 在MATLAB中创建M程序和M函数的方法是相同的. 点击菜单“File→New → M-File”, 打开文本编辑器, 程序编写完成后, 点击 按纽         即可执行.  程序的输出结果在命令窗口.
• 通常用户建立的M程序和M函数存放在当前目录中, MATLAB可以自动搜索到.

(1) M程序

M程序特征：

由一般语句组成, 程序中的变量是全局的, 可以在MATLAB命令窗口输入文件名来执行.

举例：

%列出一个求fibonnaci数的程序, 它是一个数列, 从[1，1]开始, 由数列的最后两个元素之和生成新的元素, 依次递推

f=[1,1]; 
i=1;
N=10;
while f(i)+f(i+1)<N  %循环条件检验
    f(i+2)=f(i+1)+f(i); %求fibonnaci数的算式
    i=i+1;  
end
f
得到：
f =

     1     1     2     3     5     8

 (2) M函数

M函数特征：

1. 由function起头, 后面跟的函数名, 函数名必须与文件名相同.
2. 有输入输出变量, 可以进行变量传递.
3. 除非用global声明, 程序中的变量均为局部变量, 不保存在工作空间中.
4. M函数不能独立运行, 必须由其它程序调用.

一般格式：function y=FunctionName(x)

举例：

%求fibonnaci数的函数
function f = fib(n)
if n <= 2
    f = 1;
else
    f = fib(n-1) + fib(n-2);
end