题目：

链接：剑指 Offer 15. 二进制中1的个数；LeetCode 191. 位1的个数
难度：简单

编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为汉明重量）。

提示：

• 请注意，在某些语言（如 Java）中，没有无符号整数类型。在这种情况下，输入和输出都将被指定为有符号整数类型，并且不应影响您的实现，因为无论整数是有符号的还是无符号的，其内部的二进制表示形式都是相同的。
• 在 Java 中，编译器使用二进制补码记法来表示有符号整数。因此，在 示例 3 中，输入表示有符号整数 -3。

示例 1：

输入：n = 00000000000000000000000000001011
输出：3
解释：输入的二进制串 00000000000000000000000000001011 中，共有三位为 ‘1’。

示例 2：

输入：n = 00000000000000000000000010000000
输出：1
解释：输入的二进制串 00000000000000000000000010000000 中，共有一位为 ‘1’。

示例 3：

输入：n = 11111111111111111111111111111101
输出：31
解释：输入的二进制串 11111111111111111111111111111101 中，共有 31 位为 ‘1’。

提示：

• 输入必须是长度为 32 的 二进制串 。

进阶：

• 如果多次调用这个函数，你将如何优化你的算法？

位运算：

第一种写法，如代码一，对这个数字每次右移一位并用与运算&检查最后一位是不是1，统计1的个数。

第二种写法，n & (n - 1) 是一种消除数字二进制表示中最后一个1的小技巧，如图：

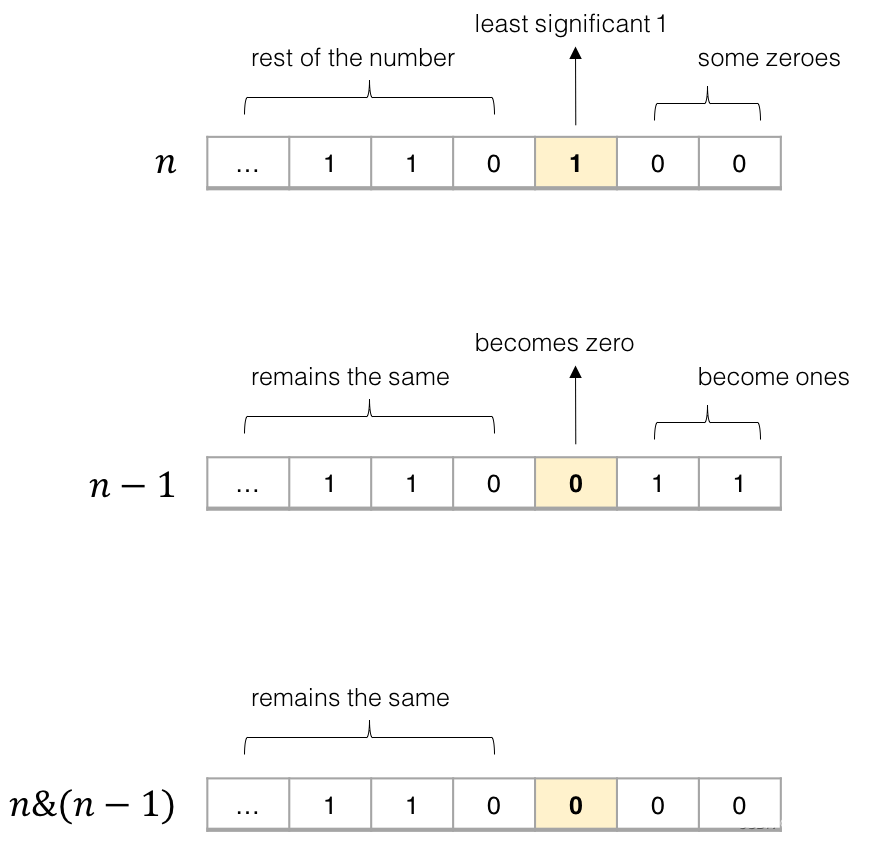
代码一：

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int sum = 0;
        for(int i = 0; i < 32; i++)
        {
            if(n & 1) sum++;  // 最后一位是不是1
            n >>= 1;  // 右移一位
        }
        return sum;
    }
};

时间复杂度O(k)，k是二进制的位数，即32。
空间复杂度O(1)。

代码二（优化）：

class Solution {
public:
    int hammingWeight(uint32_t n) {
        int sum = 0;
        while(n) {
            n &= (n - 1);  // 这个操作每次可以消掉一个最末位的1
            sum++;
        }
        return sum;
    }
};

时间复杂度O(logN)，N是二进制位中1的个数，最坏情况下全部为1，那时间复杂度将等于代码一。
空间复杂度O(1)。