Interpolation Across Triangles: Barycentric Coordinates(重心坐标)

Interpolation Across Triangles(三角形内的插值)

Why do we want to interpolate(我们为什么要在三角形内插值)

• 我们知道三角形顶点的属性
• 希望在三角形内部每个点得到一个值，并且从一个点到另一个点是一个平滑的过渡。

What do we want to interpolate?(我们想插值得到什么？)

• 纹理坐标，颜色，法向量 …

How do we interpolate? (我们如何插值呢？)

通过重心坐标

Barycentric Coordinates(重心坐标)

重心坐标是针对三角形的，每个三角形可以定义一套重心坐标，换一个三角形就是另外一套重心坐标了。

在三角形$ABC$形成的平面内的任何一个点，都可以表示成如下形式：

$(x,y)=\alpha A+\beta B+\gamma C$

其中$\alpha +\beta +\gamma =1$

用这三个系数来描述一个点。

如果这个点在三角形内部，还需要满足另外一个条件：

这三个系数均非负

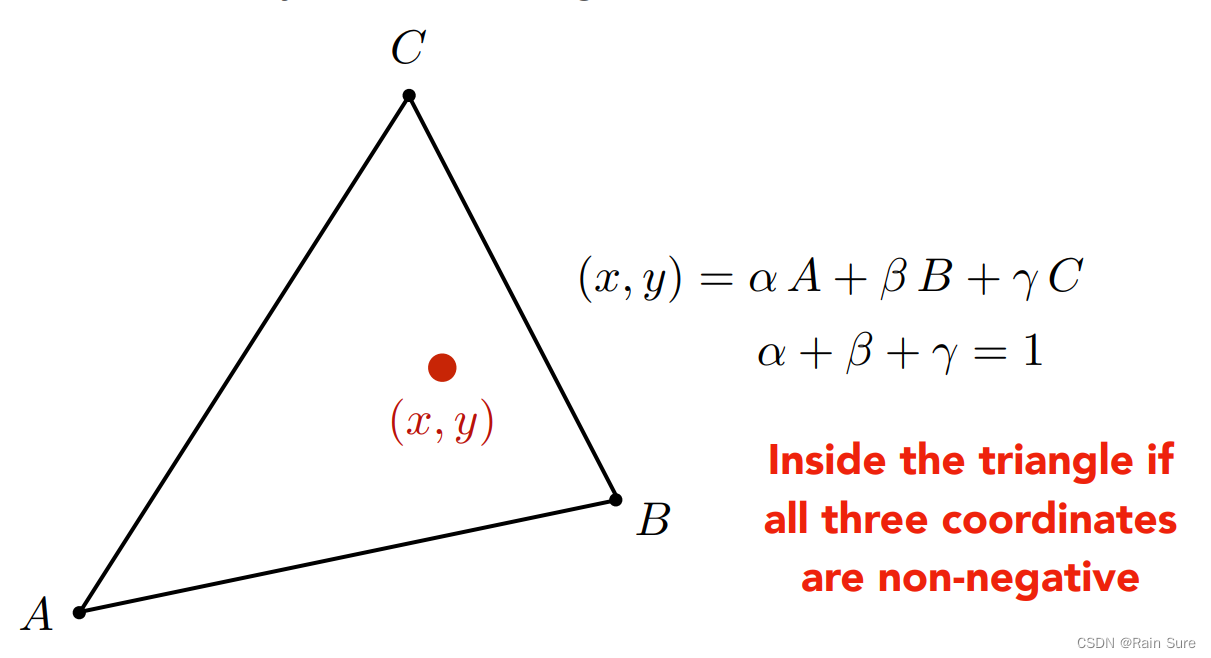
举例：

点$A$的重心坐标是什么？

是$(1,0,0)$

求任意一个点的重心坐标方法：

利用面积比

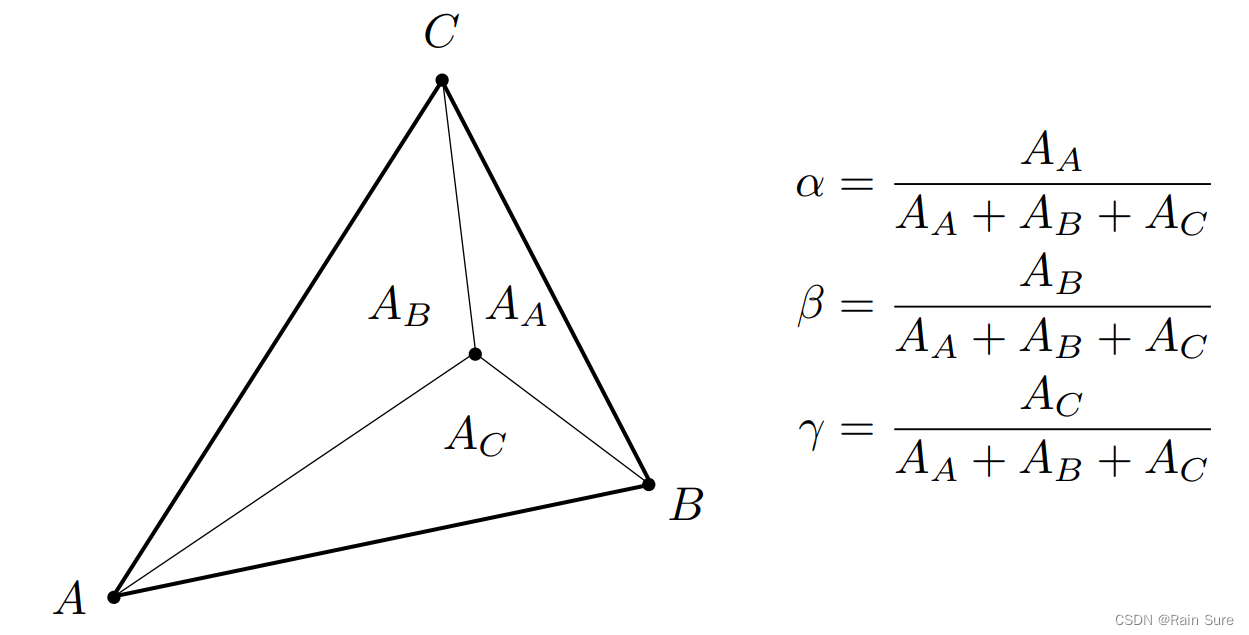
三角形自己的重心的重心坐标是多少？

是$(\frac{1}{3},\frac{1}{3},\frac{1}{3})$，因为重心有一个很好的性质，将其分别于$A$, $B$, $C$三个点连边，可以把三角形均等地分成3个面积相等的部分。

因此，重心的重心坐标就是$(\frac{1}{3},\frac{1}{3},\frac{1}{3})$。

更简便的计算重心坐标的方法：

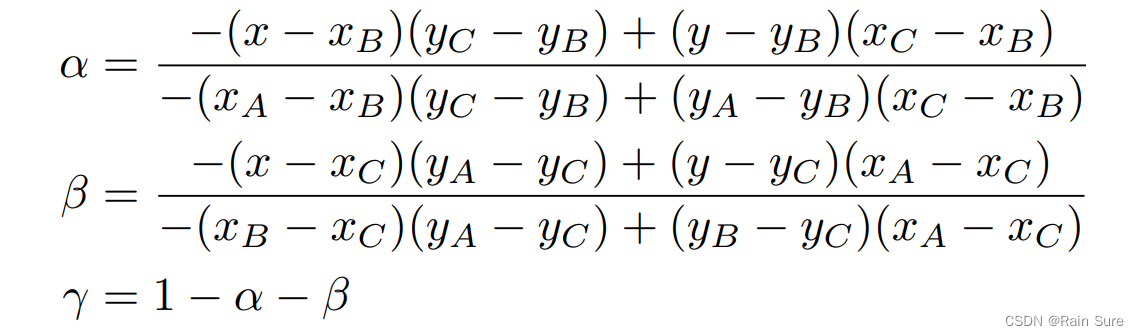
Using Barycentric Coordinates(利用重心坐标)

去算任意一个点的值，线性插值。

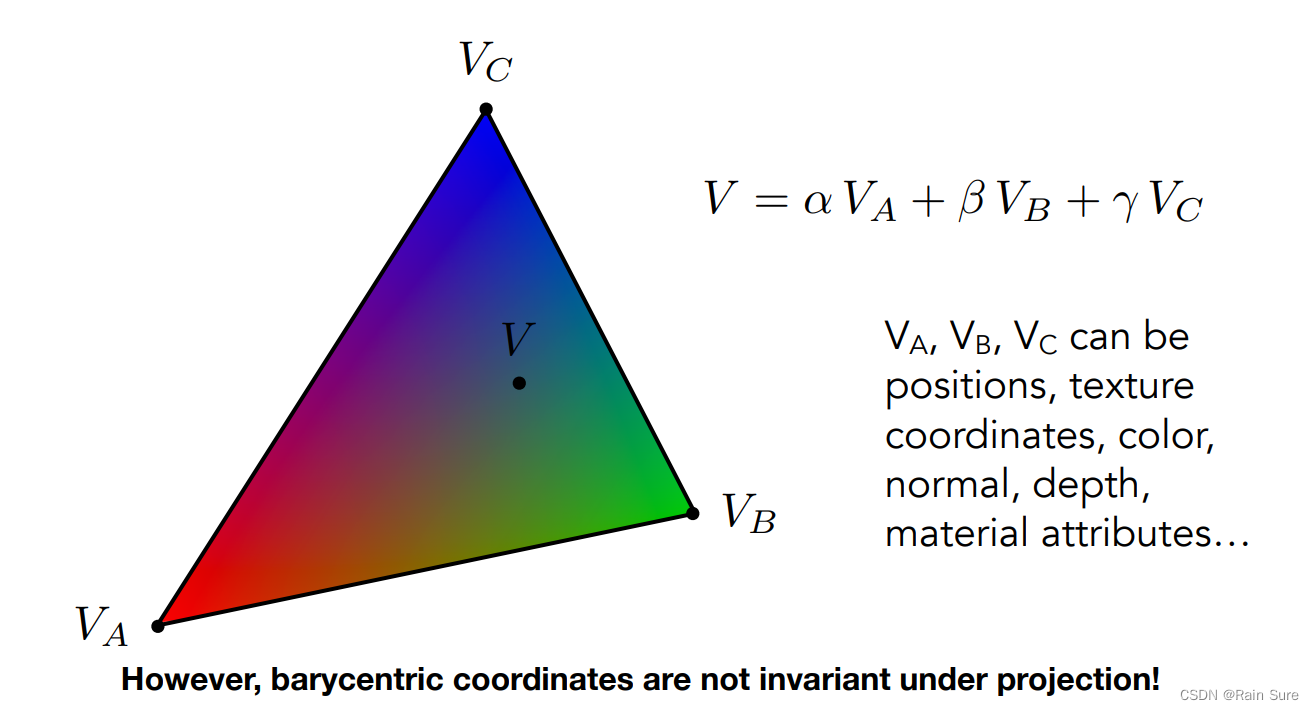
注意：投影之后的计算的重心坐标和原始计算出的重心坐标是不同的，这就启发我们，在计算三维空间中的属性时，需要保持在三维空间中计算。

Applying Textures(应用纹理)

Simple Texture Mapping: Diffuse Color(简单的纹理映射：漫反射颜色)

对于屏幕上的每个像素$(x,y)$，计算出它的纹理坐标$(u,v)$，从纹理图中获取这个点的颜色，然后给这个像素赋予这个颜色。

Texture Magnification(纹理放大)

What if the texture is too small?(纹理太小了怎么办？)

纹理太小了会出现什么情况？

计算得到的纹理坐标是一个非整数的值，可以直接将其四舍五入进行计算。

但是这样操作的话，很多个像素(pixel)会被映射到同一个texel(纹理元素)上。

Bilinear interpolation(双线性插值)

对于每四个texel，我们可以进行一次双线性插值，这样计算的结果更加准确：

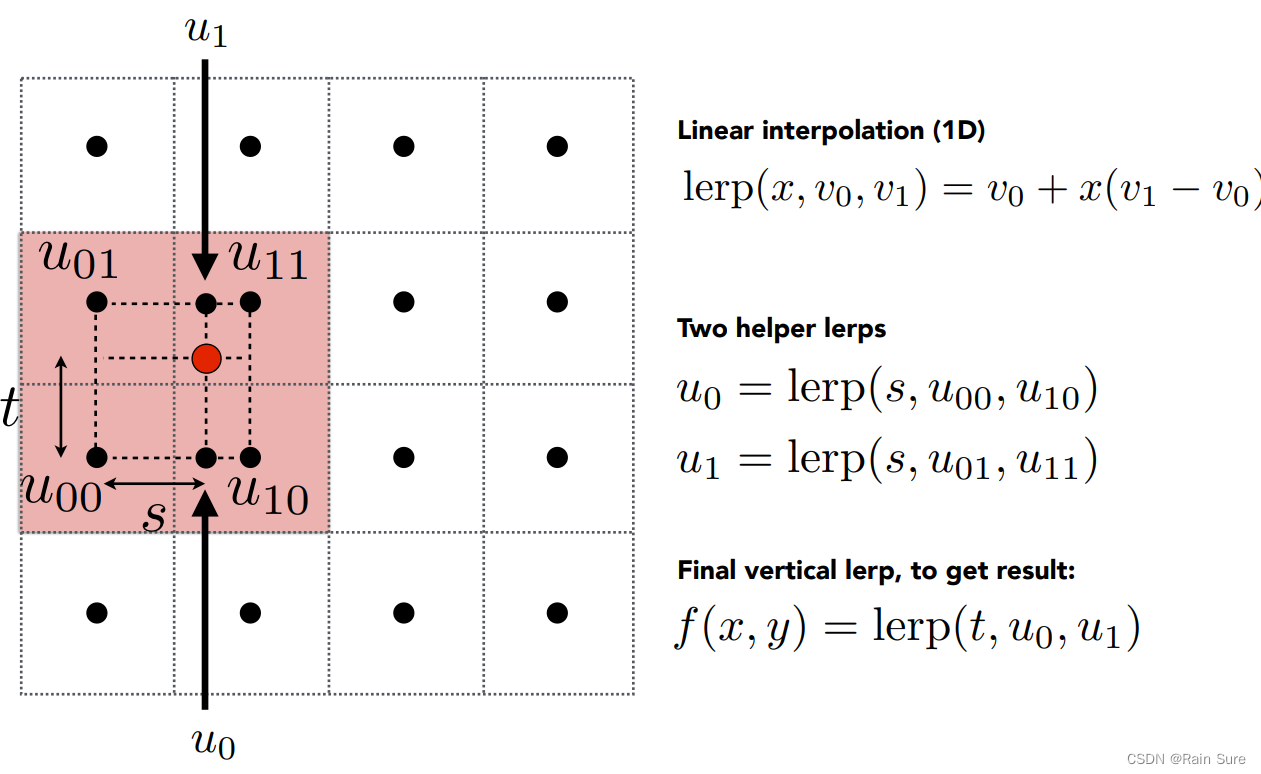
水平做了一趟插值，竖直做了一趟插值，因此叫做双线性插值。

What if the texture is too large? (纹理太大了怎么办？)

例如：出现了摩尔纹

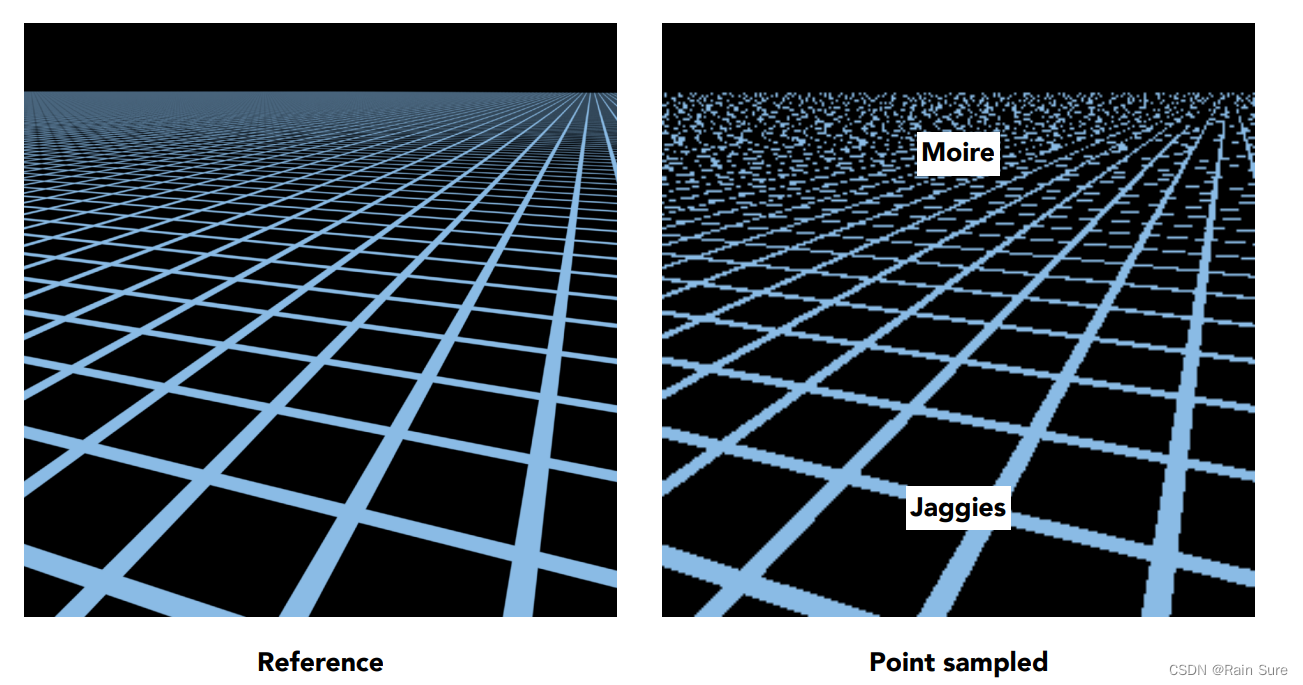
原因：

近处的像素覆盖较少的区域，远处的像素覆盖较大的区域。

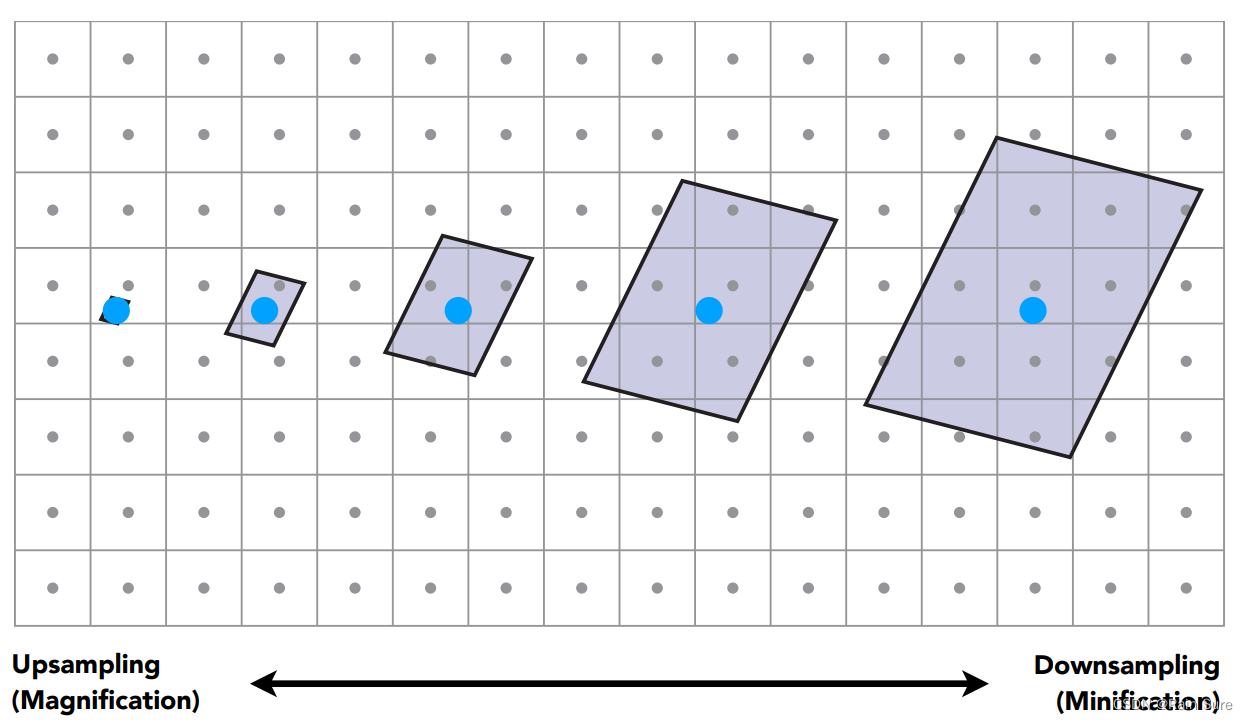
超采样可以很好的解决这种问题，但是代价太高了，算法会变的特别慢。

思考一下，有没有方法可以帮助我们快速得到一个范围内的平均值？

Mipmap (支持快速，近似，方形的范围查询)

首先，预处理这些级别的纹理图：

总存储量是原来的$\frac{4}{3}$。

计算一个像素在纹理图中占据的大小：

考虑四个相邻的点，将其映射到纹理中，得到它们的纹理坐标，计算出一个最大的边长，将其视作正方形的边长。

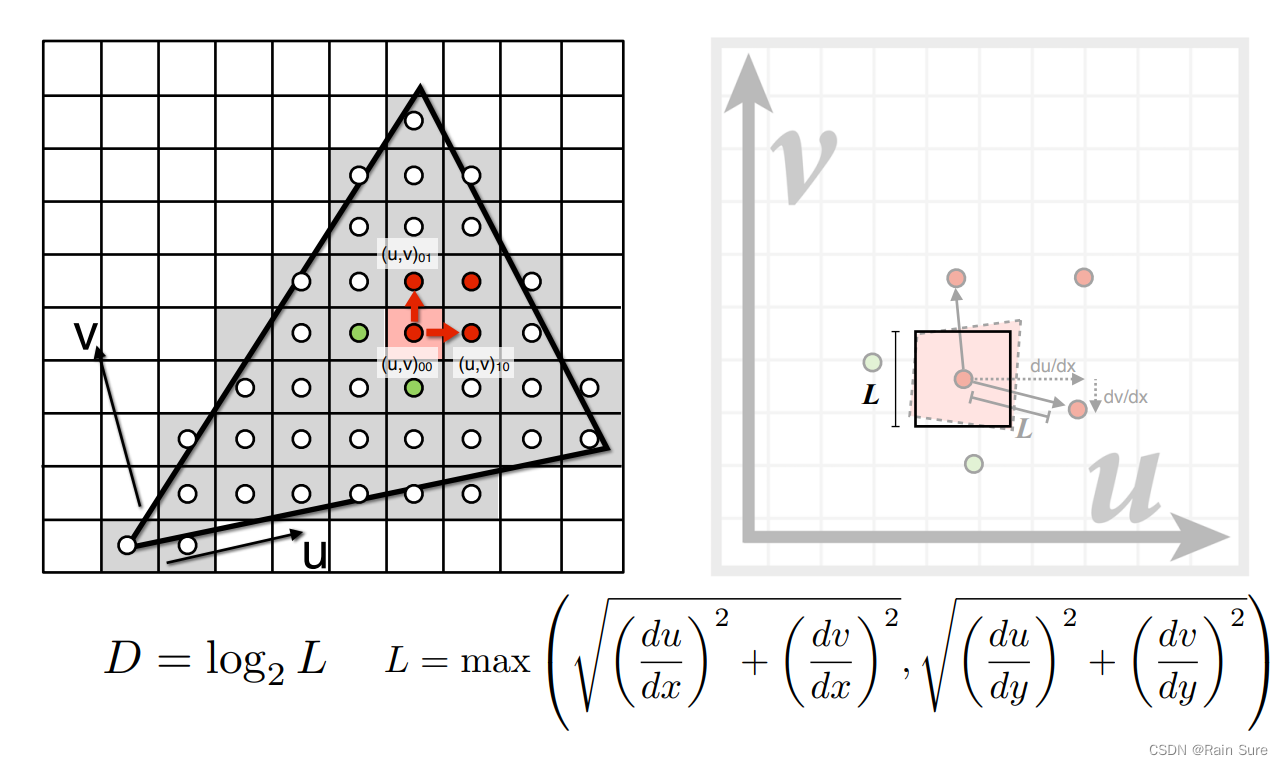
假如这个正方形的边长是4，那么我们就可以知道这个区域在$D=2$的时候就会变成一个像素。

我们就可以去查那个像素，就可以立即得到这个区域的平均值。

但是这样操作，可能会出现不连续的情况。

解决方法：插值

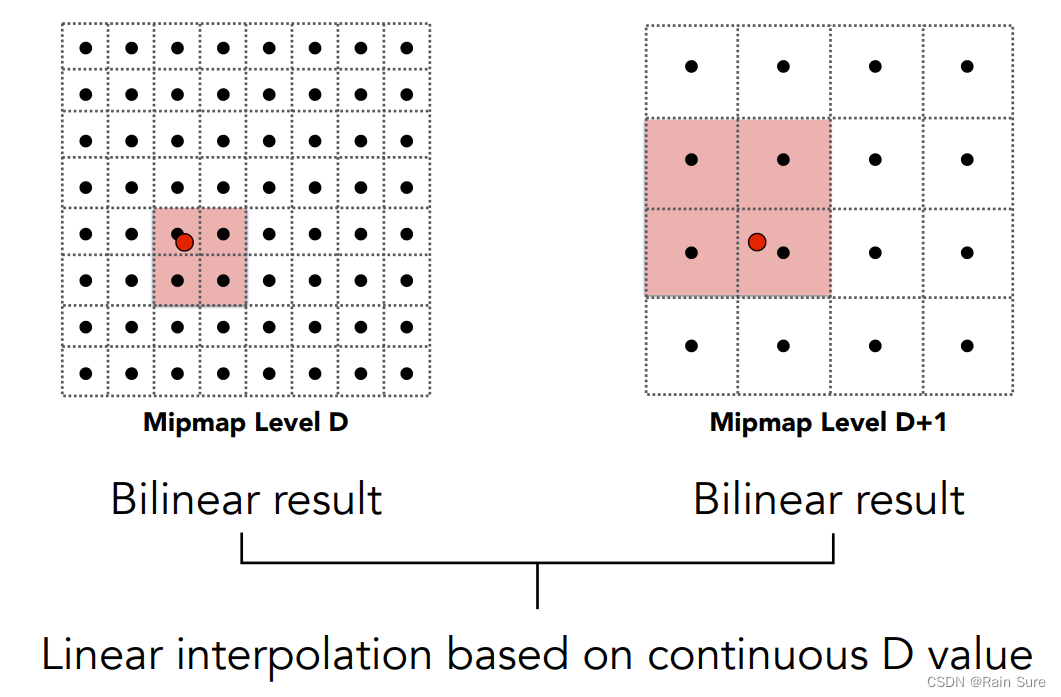
三线性插值：

先在层内部进行双线性插值，再在层与层之间再做一次线性插值。

总共做了三趟插值，所以叫做三线性插值。

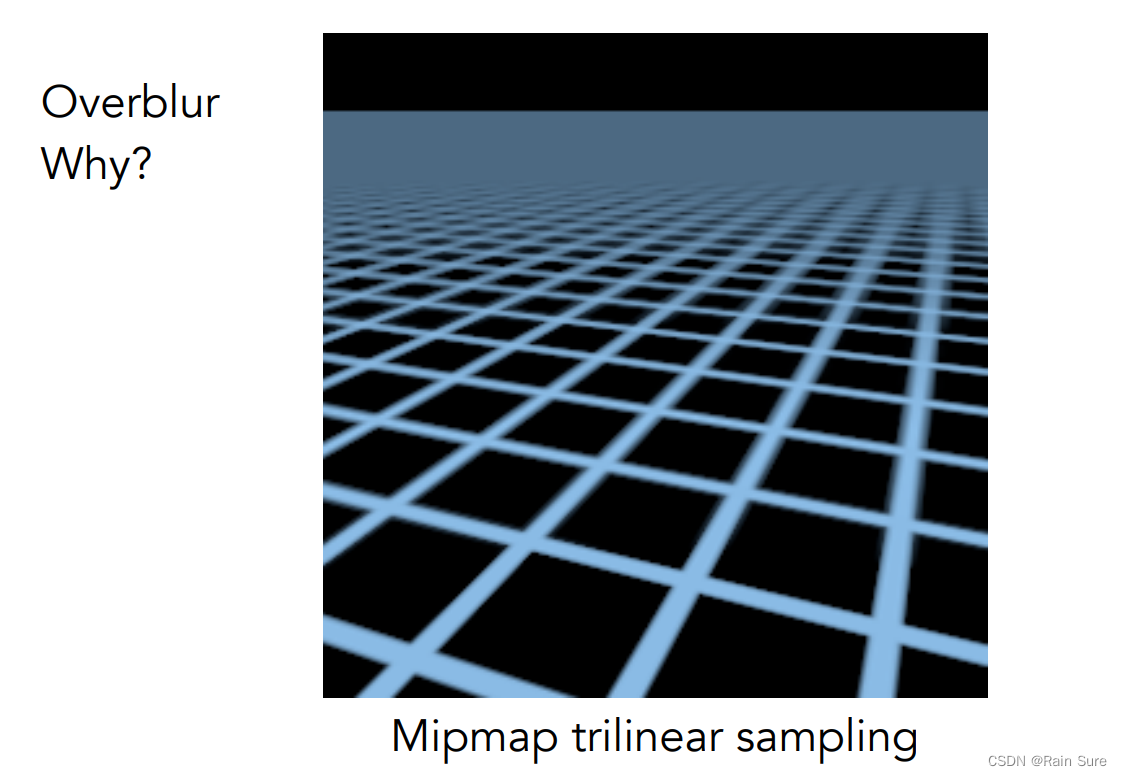
缺点：MipMap在远处的时候，会出现糊掉的情况(Overblur):

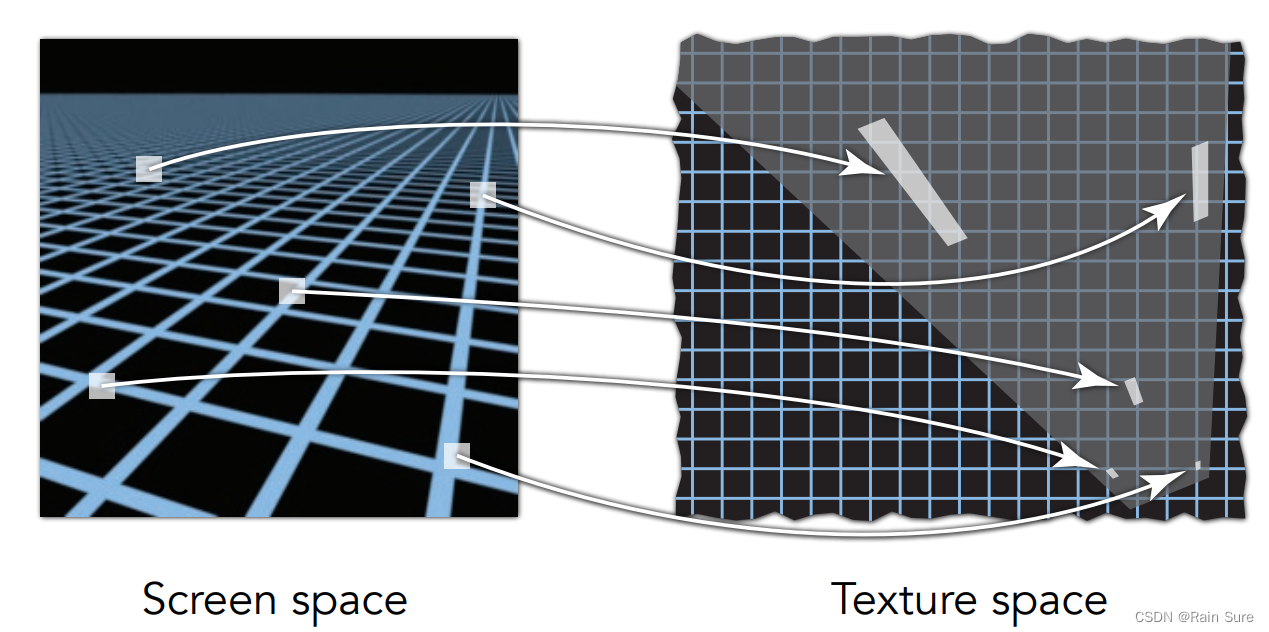
解决方法：各向异性过滤

预处理出来，水平和竖直方向分别压缩的情况：这样就可以得到一个矩形的平均值，而不仅仅限制于一个正方形区域。

但是针对某些特殊情况，例如斜着的长条举行，各向异性过滤仍然不能很好地解决：

另一种解决方法：EWA过滤：

通过分解成多个椭圆来进行查询

缺点是需要多次查询

参考资源

GAMES101 Lecture 09