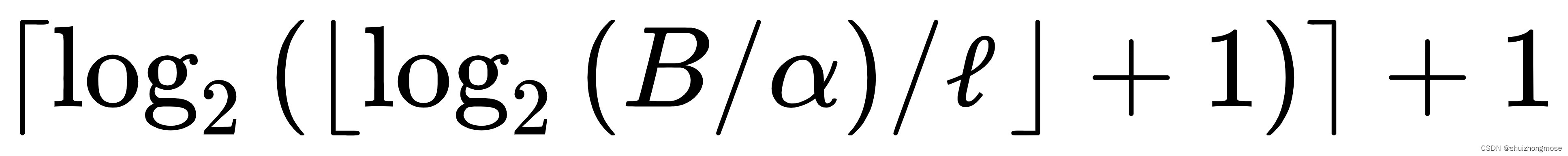1 知识预警
1.1 线性代数
(
A
T
)
T
=
A
(A^\mathrm{T})^\mathrm{T}=A
(AT)T=A$
(
A
+
B
)
T
=
A
T
+
B
T
(A+B)^\mathrm{T}=A^\mathrm{T}+B^\mathrm{T}
(A+B)T=AT+BT
(
λ
A
)
T
=
λ
A
T
(\lambda A)^\mathrm{T}=\lambda A^\mathrm{T}
(λA)T=λAT
(
A
B
)
T
=
B
T
A
T
(AB)^\mathrm{T}=B^\mathrm{T}A^\mathrm{T}
(AB)T=BTAT
(
A
−
1
)
−
1
=
A
(A^{-1})^{-1}=A
(A−1)−1=A
(
A
B
)
−
1
=
B
−
1
A
−
1
(AB)^{-1}=B^{-1}A^{-1}
(AB)−1=B−1A−1
1.2 矩阵微积分
为了书写简便,我们通常把单个函数对多个变量或者多元函数对单个变量的偏导数写成向量和矩阵的形式,使其可以被当成一个整体处理.矩阵微积分(Matrix Calculus)是多元微积分的一种表达方式,即使用矩阵和向量来表示因变量每个成分关于自变量每个成分的偏导数。
标量关于向量的偏导数:对于M维向量 x ∈ R x \in \mathbb{R} x∈R和函数 y = f ( x ) ∈ R y=f(x) \in \mathbb{R} y=f(x)∈R,则关于 x x x的偏导数为:
∂
y
∂
x
=
[
∂
y
∂
x
1
,
⋯
,
∂
y
∂
x
M
]
⊤
∈
R
M
×
1
,
\frac{\partial y}{\partial \boldsymbol{x}}=\left[\frac{\partial y}{\partial x_{1}}, \cdots, \frac{\partial y}{\partial x_{M}}\right]^{\top} \quad \in \mathbb{R}^{M \times 1},
∂x∂y=[∂x1∂y,⋯,∂xM∂y]⊤∈RM×1,
向量关于标量的偏导数:对于标量𝑥 ∈ ℝ和函数𝒚 = 𝑓(𝑥) ∈
R
N
\mathbb{R}^N
RN,则𝒚关于𝑥 的
偏导数为
∂
y
∂
x
=
[
∂
y
1
∂
x
,
⋯
,
∂
y
N
∂
x
]
∈
R
1
×
N
\frac{\partial \boldsymbol{y}}{\partial x}=\left[\frac{\partial y_{1}}{\partial x}, \cdots, \frac{\partial y_{N}}{\partial x}\right] \quad \in \mathbb{R}^{1 \times N}
∂x∂y=[∂x∂y1,⋯,∂x∂yN]∈R1×N
向量关于向量的偏导数 对于 𝑀 维向量 𝒙 ∈ ℝ𝑀 和函数 𝒚 = 𝑓(𝒙) ∈ ℝ𝑁,则
𝑓(𝒙)关于𝒙的偏导数(分母布局)为
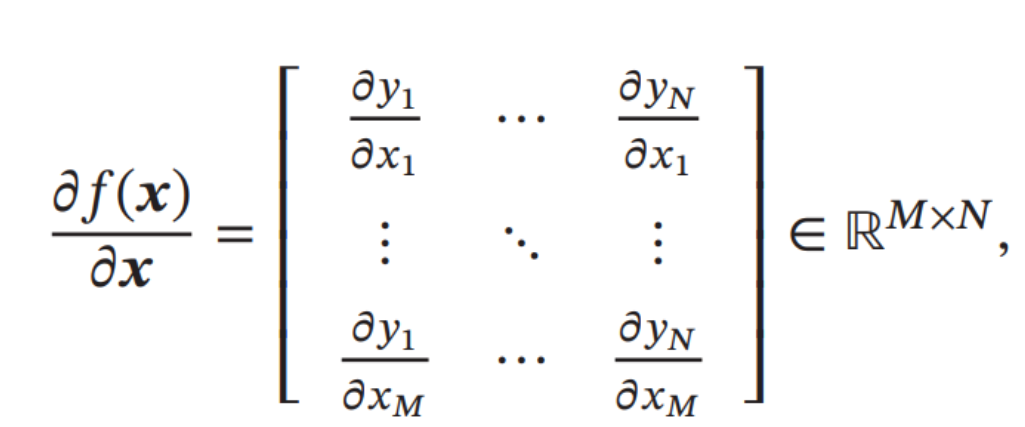
向量函数及其导数
∂
x
∂
x
=
I
\frac{\partial \pmb x}{\partial \pmb x} = I
∂x∂x=I
∂
A
x
∂
x
=
A
T
\frac{\partial \pmb A \pmb x}{\partial \pmb x} = \pmb A^\mathrm{T}
∂x∂Ax=AT
∂
x
T
A
∂
x
=
A
\frac{ \partial \pmb x^\mathrm{T} A}{\partial \pmb x} = \pmb A
∂x∂xTA=A
2 什么是回归分析?
回归分析这是一个来自统计学的概念。回归分析是指一种预测性的建模技术,主要是研究自变量和因变量的关系。通常使用线/曲线来拟合数据点,然后研究如何使曲线到数据点的距离差异最小。如果使用直线进行拟合,则为线性回归(一元线性回归、多元线性回归);如果是对非线性关系进行建模,则为多项式回归。
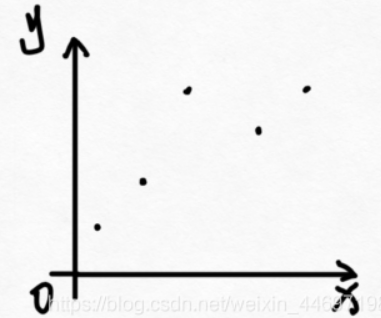
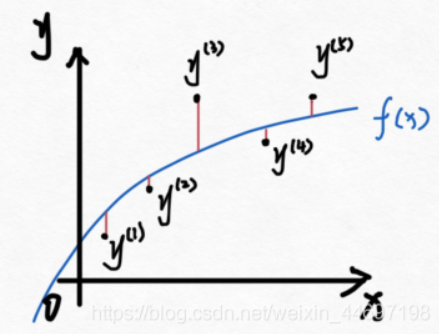
例如,存在以下数据(左图)。然后我们拟合一条曲线
f
(
x
)
f(x)
f(x)右图,回归分析的目标就是要拟合一条曲线,让图中红色线段加起来的和最小。
3 线性回归
线性回归(Linear Regression)是回归分析的一种,是机器学习和统计学中最基础和最广泛应
用的模型,是一种对自变量和因变量之间关系进行建模的回归分析.自变量数量为1时称为简单回归,自变量数量大于1时称为多元回归。
-
假设目标值(因变量)与特征值(自变量)之间线性相关,即满足一个多元一次方程,如: f ( x ) = ( w 1 x 1 + … + w n x n + b ) f(x)=(w_1x_1+…+w_nx_n+b) f(x)=(w1x1+…+wnxn+b)。
-
然后构建损失函数。
-
最后通过令损失函数最小来确定参数。(最关键的一步)
3.1 一元线性回归
一元线性回归(一元:只有一个未知自变量;线性:自变量 x x x的次数都为1次)。
f
(
x
)
=
w
x
+
b
\begin{align} f(x)=wx+b \end{align}
f(x)=wx+b
有
N
N
N组数据,自变量
x
=
(
x
(
1
)
,
x
(
2
)
,
…
,
x
(
n
)
)
x=(x^{(1)},x^{(2)},…,x^{(n)})
x=(x(1),x(2),…,x(n)),因变量
y
=
(
y
(
1
)
,
y
(
2
)
,
…
,
y
(
n
)
)
y=(y^{(1)},y^{(2)},…,y^{(n)})
y=(y(1),y(2),…,y(n)),则训练集
D
=
{
(
x
(
n
)
,
y
(
n
)
)
}
n
=
1
N
\mathcal{D}=\{(x^{(n)} ,y^{(n)})\}_{n=1}^N
D={(x(n),y(n))}n=1N,然后我们假设它们之间的关系是:
y
^
(
n
)
=
f
(
x
)
=
w
x
(
n
)
+
b
\begin{align}\hat y^{(n)}=f(x)=wx^{(n)}+b \end{align}
y^(n)=f(x)=wx(n)+b
那么线性回归的目标就是如何让
f
(
x
)
f(x)
f(x)和
y
y
y之间的差异最小,换句话说就是
a
a
a,
b
b
b取什么值的时候
f
(
x
)
f(x)
f(x)和
y
y
y最接近。
这里我们得先解决另一个问题,就是如何衡量
f
(
x
)
f(x)
f(x)和
y
y
y之间的差异。在回归问题中,均方误差是回归任务中最常用的性能度量。记
J
(
a
,
b
)
J(a,b)
J(a,b)为
f
(
x
)
f(x)
f(x)和
y
y
y之间的差异,即预测值和真实值的差异:
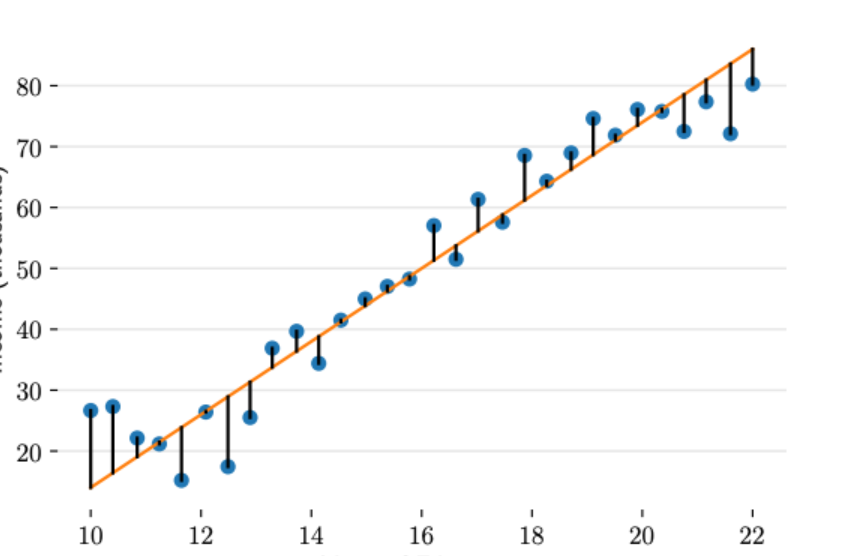
给定一组包含N个训练样本的数据集 D = { ( x ( n ) , y ( n ) ) } n = 1 N \mathcal{D}=\{(x^{(n)} ,y^{(n)})\}_{n=1}^N D={(x(n),y(n))}n=1N,则假设函数为:
L
(
w
,
b
)
=
∑
i
=
1
N
(
f
(
x
(
n
)
)
−
y
(
n
)
)
2
=
(
w
x
(
n
)
+
b
−
y
(
n
)
)
2
\begin{align} \mathcal{L}(w,b) &=\sum_{i=1}^N \left(f(x^{(n)}) - y^{(n)}\right)^2 \\ &=(wx^{(n)}+b-y^{(n)})^2 \end{align}
L(w,b)=i=1∑N(f(x(n))−y(n))2=(wx(n)+b−y(n))2
这里称
L
(
w
,
b
)
\mathcal{L}(w,b)
L(w,b)为损失函数,明显可以看出
L
(
w
,
b
)
\mathcal{L}(w,b)
L(w,b)是二次函数,所以有最小值。当
L
(
w
,
b
)
\mathcal{L}(w,b)
L(w,b)取最小值的时候,
f
(
x
)
f(x)
f(x)和
y
y
y的差异最小,然后我们可以通过最小化
L
(
w
,
b
)
\mathcal{L}(w,b)
L(w,b)来确定
a
a
a和
b
b
b的值。求解该问题有很多方法,首先可以想到求偏导。
3.2 多元线性回归
现实中的数据可能是比较复杂的,自变量也可能不止一个,例如,影响房屋价格也很可能不止房屋面积一个因素,可能还有是否在地铁附近,房间数,层数,建筑年代等诸多因素,表示为
x
=
(
x
1
,
x
2
,
.
.
.
,
x
D
)
x=(x_1,x_2,...,x_D)
x=(x1,x2,...,xD)。不过,这些因素对房价影响的权重是不同的,因此,我们可以使用多个权重
w
=
(
w
1
,
w
2
,
.
.
.
,
w
D
)
w=(w_1,w_2,...,w_D)
w=(w1,w2,...,wD)来表示多个因素与房屋价格的关系:
y
^
=
f
(
x
)
=
(
w
1
x
1
+
…
+
w
D
x
D
+
b
)
\begin{align} \hat{y}=f(x)&=(w_1x_1+…+w_Dx_D+b)\\ \end{align}
y^=f(x)=(w1x1+…+wDxD+b)
给定一组包含
N
N
N个训练样本的数据集
D
=
{
(
x
(
n
)
,
y
(
n
)
)
}
n
=
1
N
\mathcal{D}=\{(x^{(n)} ,y^{(n)})\}_{n=1}^N
D={(x(n),y(n))}n=1N,则假设函数为:
y
^
(
n
)
=
f
(
x
)
=
(
w
1
x
1
(
n
)
+
w
2
x
2
(
n
)
+
…
+
w
D
x
D
(
n
)
+
b
)
=
∑
d
=
1
D
w
d
x
d
(
n
)
+
b
\begin{align} \hat{y}^{(n)}=f(x) &=(w_1x_1^{(n)}+w_2x_2^{(n)}+…+w_Dx_D^{(n)}+b) \\ &= \sum_{d=1}^Dw_dx_d^{(n)}+b \end{align}
y^(n)=f(x)=(w1x1(n)+w2x2(n)+…+wDxD(n)+b)=d=1∑Dwdxd(n)+b
写成向量形式:
y ^ ( n ) = f ( x ( n ) ) = w x ( n ) + b \begin{align} \hat{\pmb{y}}^{(n)}=f( \pmb{x}^{(n)})=\pmb{w} \pmb{x}^{(n)}+b \end{align} y^(n)=f(x(n))=wx(n)+b
为表示方便,重新定义向量 w : = w ⨁ b = [ w 1 w 2 ⋮ w D b ] \pmb w:= \pmb w \bigoplus b=\begin{bmatrix} w_{1} \\ w_{2} \\ {\vdots}\\ w_{D} \\ b \\ \end{bmatrix} w:=w⨁b= w1w2⋮wDb , x : = x ⨁ 1 = [ x 1 x 2 ⋮ x D 1 ] \pmb x:=\pmb x \bigoplus 1=\begin{bmatrix} x_{1} \\ x_{2} \\ {\vdots}\\ x_{D} \\ 1 \\ \end{bmatrix} x:=x⨁1= x1x2⋮xD1 ,写成增广向量的形式:
y ^ = f ( x ) = w T x \begin{align} \hat{\pmb{y}}=f( \pmb{x})=\pmb{w ^\mathrm T} \pmb{x} \end{align} y^=f(x)=wTx
尽管公式 ( 7 ) (7) (7)可以描述变量之间的关系,但是一般机器学习领域更喜欢使用公式 ( 9 ) (9) (9)这样的向量乘法的形式。这不仅因为这样表示起来更简单,也是因为现代计算机对向量计算做了大量优化,无论是CPU还是GPU都喜欢向量计算,并行地处理数据,可以得到成百上千倍的加速比。需要注意的是,公式中不加粗的表示标量,加粗的表示向量或矩阵。
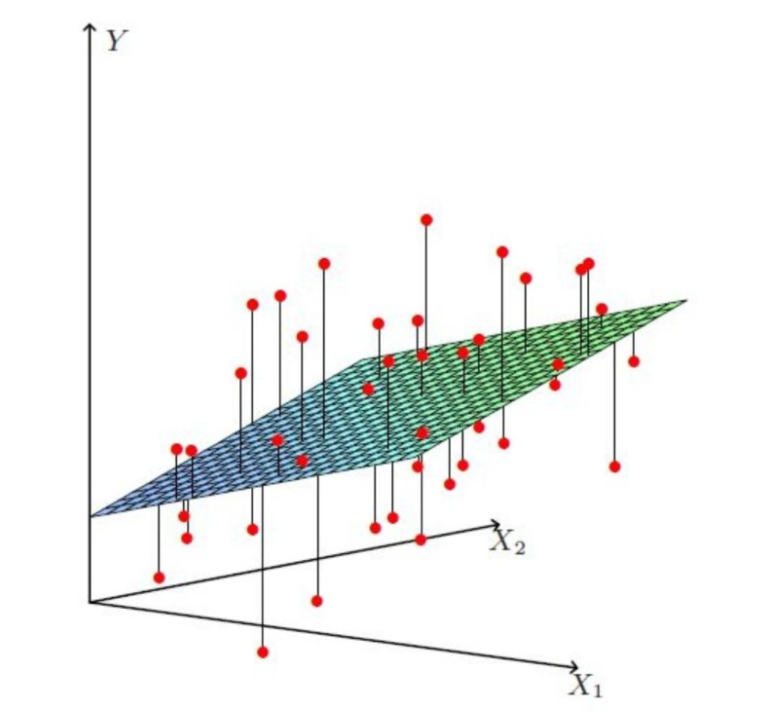
比一元线性回归更为复杂的是,多元线性回归组成的不是直线,是一个多维空间中的超平面,数据点散落在超平面的两侧。多元线性回归的损失函数仍然使用预测值-真实值的平方来计算,损失函数为所有样本点距离超平面的距离之和:
L ( w , b ) = ∑ n = 1 N ( f ( x ( n ) ) − y ( n ) ) 2 = ∑ n = 1 N ( w 1 x 1 ( n ) + w 2 x 2 ( n ) + + … + w D x D ( n ) + b − y ( n ) ) 2 = ∑ n = 1 N ( ( ∑ d = 1 D w d x d ( n ) + b ) − y ( n ) ) 2 ⟺ 1 2 ∑ n = 1 N ( ( ∑ d = 1 D w d x d ( n ) + b ) − y ( n ) ) 2 \begin{align} \mathcal{L}(w,b) &=\sum_{n=1}^N \left(f(x^{(n)}) - y^{(n)}\right)^2 \\ &=\sum_{n=1}^N(w_1x_1^{(n)}+w_2x_2^{(n)}++…+w_Dx_D^{(n)}+b -y^{(n)})^2\\ &=\sum_{n=1}^N \left( \left( \sum_{d=1}^Dw_dx_d^{(n)}+b \right)-y^{(n)} \right)^2\\ &\iff \textcolor{red}{\frac{1}{2} }\sum_{n=1}^N \left( \left( \sum_{d=1}^Dw_dx_d^{(n)}+b \right)-y^{(n)} \right)^2\\ \end{align} L(w,b)=n=1∑N(f(x(n))−y(n))2=n=1∑N(w1x1(n)+w2x2(n)++…+wDxD(n)+b−y(n))2=n=1∑N((d=1∑Dwdxd(n)+b)−y(n))2⟺21n=1∑N((d=1∑Dwdxd(n)+b)−y(n))2
写成矩阵形式,令
X
=
[
x
1
(
1
)
x
1
(
2
)
…
x
1
(
N
)
x
2
(
1
)
x
2
(
2
)
…
x
2
(
N
)
⋮
⋮
⋮
⋮
x
D
(
1
)
x
D
(
2
)
…
x
D
(
N
)
1
1
…
1
]
\pmb X=\begin{bmatrix} x_{1}^{(1)} & x_{1}^{(2)} & {\dots} &x_{1}^{(N)}\\ x_{2}^{(1)} & x_{2}^{(2)} & {\dots} &x_{2}^{(N)}\\ {\vdots} & {\vdots} & {\vdots} & {\vdots}\\ x_{D}^{(1)} &x_{D}^{(2)} & {\dots}&x_{D}^{(N)} \\ 1 & 1 & {\dots} & 1\\ \end{bmatrix}
X=
x1(1)x2(1)⋮xD(1)1x1(2)x2(2)⋮xD(2)1……⋮……x1(N)x2(N)⋮xD(N)1
,
X
\pmb X
X的每一列代表一个样本,
y
=
[
y
(
1
)
y
(
2
)
⋮
y
(
N
)
]
\pmb y=\begin{bmatrix} y^{(1)}\\y^{(2)}\\ \vdots \\y^{(N)}\end{bmatrix}
y=
y(1)y(2)⋮y(N)
则写成矩阵形式:
L
(
w
)
=
1
2
(
X
T
w
−
y
)
T
(
X
T
w
−
y
)
=
1
2
∣
∣
X
T
w
−
y
∣
∣
2
\begin{align} \mathcal{L}(w) &=\frac{1}{2} ( \pmb X^\mathrm{T} \pmb w- \pmb y)^\mathrm{T}( \pmb X^\mathrm{T} \pmb w- \pmb y)\\ &=\frac{1}{2} || \pmb X^\mathrm{T} \pmb w-\pmb y ||^2 \end{align}
L(w)=21(XTw−y)T(XTw−y)=21∣∣XTw−y∣∣2
目标是最小化损失函数式(15),这是一个无约束多元函数求极值问题,有梯度下降、牛顿法、共轭梯度法,智能优化算法(粒子群算法等、遗传算法、鲸鱼算法等),但首先想到的解法是求导令
∂
L
(
w
)
∂
w
=
0
\frac{\partial \mathcal L(w)}{\partial w}=0
∂w∂L(w)=0:
∂ ∂ w L ( w ) = X ( X T w − y ) = X X T w − X y = 0 X X T w = X y w = ( X X T ) − 1 X y \begin{align} \frac{\partial}{\partial w} \mathcal L(w) &=\pmb X (\pmb X^\mathrm{T} \pmb w-\pmb y)\\ &=\pmb X \pmb X^\mathrm{T}\pmb w - \pmb X\pmb y = 0 \\ \pmb X \pmb X^\mathrm{T}\pmb w&=\pmb X\pmb y\\ \pmb w&= (\pmb X \pmb X^\mathrm{T})^{-1}\pmb X \pmb y \end{align} ∂w∂L(w)XXTww=X(XTw−y)=XXTw−Xy=0=Xy=(XXT)−1Xy
以上求偏导令=0的解法,就是最小二乘法,这里的二乘表示用平方来度量观测点与估计点的远近(在古汉语中“平方”称为“二乘”);“最小”指的是参数的估计值要保证各个观测点与估计点的距离的平方和达到最小,是minimize最小化。