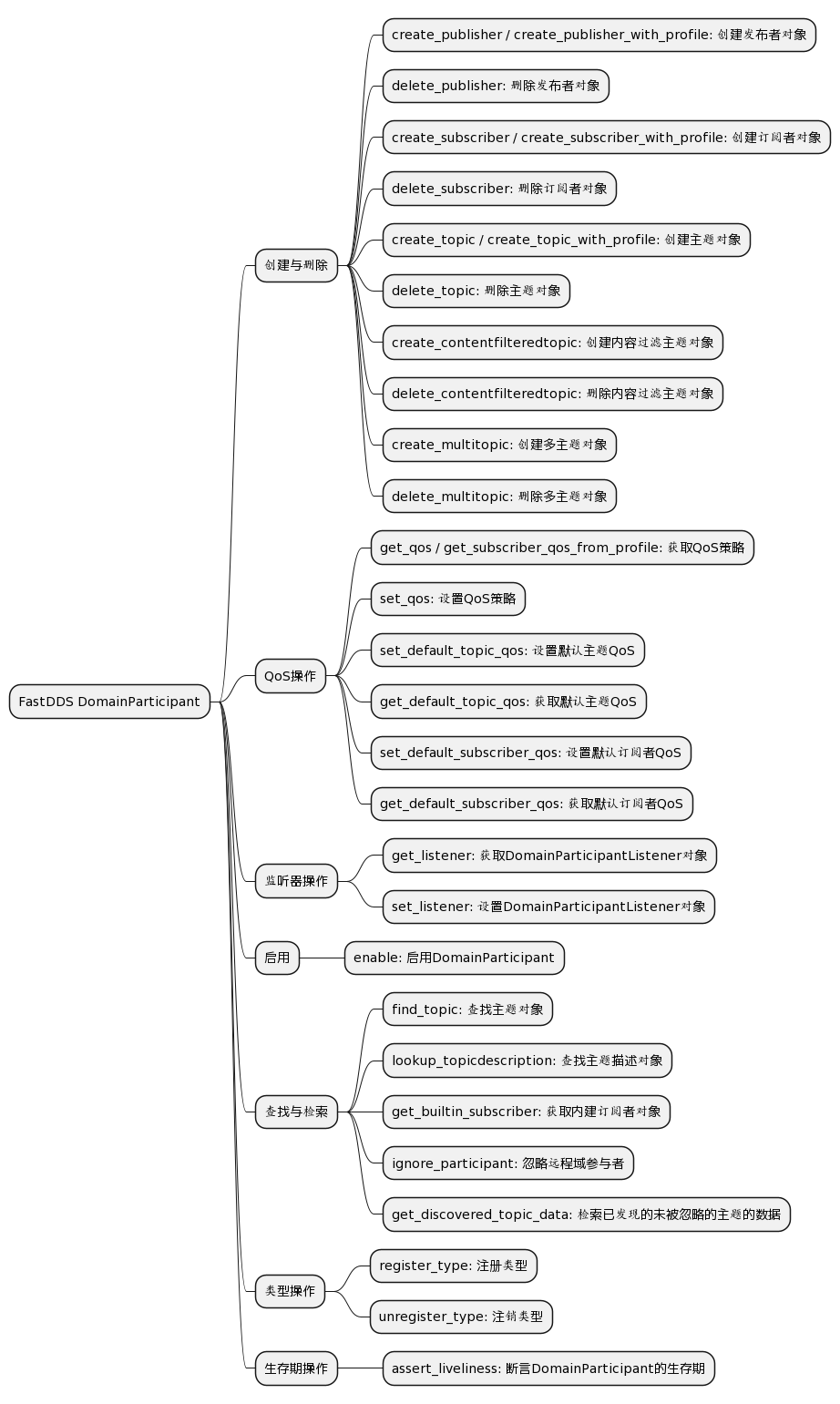
个人主页：平行线也会相交
欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创
收录于专栏【手撕算法系列专栏】【LeetCode】
🍔本专栏旨在提高自己算法能力的同时，记录一下自己的学习过程，希望对大家有所帮助
🍓希望我们一起努力、成长，共同进步。

点击直接跳转到该题目

🥙题目描述

三步问题。有个小孩正在上楼梯，楼梯有n阶台阶，小孩一次可以上1阶、2阶或3阶。实现一种方法，计算小孩有多少种上楼梯的方式。结果可能很大，你需要对结果模1000000007。
示例1：

输入：n = 3
输出：4
说明: 有四种走法

示例2：

输入：n = 5
输出：13

提示:

n范围在[1, 1000000]之间

🎂算法原理+题目解析

步骤1（最重要）状态表示

以dp[i]为结尾，dp[i]表示到达i位置时一共有多少种方法。

步骤2（最难）：状态转移方程

我们以i位置的状态，通过最近的一步或者几步来划分问题。通过题目要求，这里最近的几步分别是dp[i-3]、dp[i-2]、dp[i-1]，所以我们需要找到这几步的状态。
也就是说这里分为三种情况：
从i-3位置跳3步到达i位置，需要先经过i-3位置才能继续跳三步。假设需要x种方法，有多少种方法到达i-3位置，就有多少种方法从起点到达i位置。
从i-2位置跳2步到达i位置，需要先经过i-2位置才能继续跳二步。假设需要y种方法，有多少种方法到达i-2位置，就有多少种方法从起点到达i位置。
从i-1位置跳1步到达i位置，需要先经过i-1位置才能继续跳三步。假设需要z中方法，有多少种方法到达i-1位置，就有多少种方法从起点到达i位置。
所以，到达第i个位置的总方法数=到达i-3位置的总方法数+到达i-2位置的总方法数+到达i-1位置的总方法数。即x+y+z。我们已经知道dp[i]表示到达i位置时一共有多少种方法。所以dp[i-3]=x、dp[i-2]=y、dp[i-1]=z。
故最终的状态表示方程即：dp[i]=dp[i-3]+dp[i-2]+dp[i-1]。

步骤3：初始化

根据题目要求，dp[1]=1、dp[2]=2、dp[3]=4。

步骤4：填表顺序

我们如果想要知道dp[i]位置的状态，就需要知道dp[i-3]、dp[i-2]、dp[i-1]位置的状态，否则无法推导出dp[i]位置的状态，所以我们应该从左往右进行填表。

步骤5：返回值

由于dp[i]表示到达i位置时一共有多少种方法，所以我们直接返回dp[n]就好了。

本题尤其要注意提示部分，由于返回的数据值比较大，所以我们需要进行模运算，尤其是返回值的处理，请看：dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;这里进行模运算的时候并不是统一加完之后一起进行模运算，而每加一次dp值就需要进行模运算，即加一次dp值就需要进行一次模运算、加一次dp值就需要进行一次模运算。

🍰解题代码

class Solution {
public:
    int waysToStep(int n) {
        const int MOD =1e9+7; 
        //创建dp表
        vector<int> dp(n+1);
        
        //初始化处理边界条件
        if(n==1||n==2) return n;
        if(n==3) return 4;
        
        dp[1]=1;dp[2]=2;dp[3]=4;

        //填表
        for(int i=4; i<=n; i++)
            dp[i]=((dp[i-1]+dp[i-2])%MOD+dp[i-3])%MOD;

        //返回值
        return dp[n];
    }
};

🍱总结

该问题依然是属于动态规划类型的题目，思考的时候大体就是按照那5步（状态表示、状态转移方程、初始化来进行边界处理、填表顺序、返回值）来想，在进行代码编写的时候基本就是按照那4步进行编写（创建dp表，初始化、填表、返回值）。