1.什么是跳表-skiplist

skiplist 本质上也是一种查找结构，用于解决算法中的查找问题，跟平衡搜索树和哈希表的价值是一样的，可以作为key 或者 key/value 的查找模型。那么相比而言它的优势是什么的呢？这么等我们学习完它的细节实现，我们再来对比。skiplist是由 William Pugh 发明的，最早出现于他在 1990 年发表的论文《 Skip Lists: A Probabilistic Alternative to Balanced Trees 》。对细节感兴趣的同学可以下载论文原文来阅读。 skiplist，顾名思义，首先它是一个 list 。实际上，它是在有序链表的基础上发展起来的。如果是一个有序的链表，查找数据的时间复杂度是O(N) 。

William Pugh 开始的优化思路：

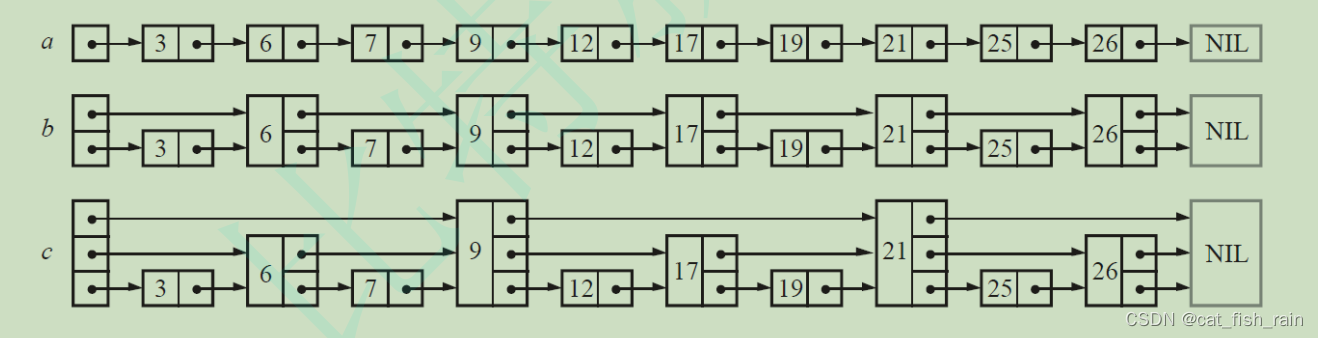
1. 假如我们 每相邻两个节点升高一层，增加一个指针，让指针指向下下个节点 ，如下图 b 所示。这样所有新增加的指针连成了一个新的链表，但它包含的节点个数只有原来的一半。由于新增加的指针，我们不再需要与链表中每个节点逐个进行比较了，需要比较的节点数大概只有原来的一半。

2. 以此类推，我们可以在第二层新产生的链表上，继续为每相邻的两个节点升高一层，增加一个指针，从而产生第三层链表。如下图c ，这样搜索效率就进一步提高了。

3. skiplist 正是受这种多层链表的想法的启发而设计出来的。实际上，按照上面生成链表的方式，上面每一层链表的节点个数，是下面一层的节点个数的一半，这样查找过程就非常类似 二分查找 ，使得查找的时间复杂度可以降低到 O(log n) 。但是这个结构在插入删除数据的时候有很大的问题 ，插入或者删除一个节点之后，就会打乱上下相邻两层链表上节点个数严格的2:1 的对应关系。如果要维持这种对应关系，就必须把新插入的节点后面的所有节点（也包括新插入的节点）重新进行调整，这会让时间复杂度重新蜕化成O(n) 。

4. skiplist 的设计为了避免这种问题，做了一个大胆的处理，不再严格要求对应比例关系，而是

插入一个节点的时候随机出一个层数。这样每次插入和删除都不需要考虑其他节点的层数，

这样就好处理多了。细节过程入下图：

2.skiplist的效率如何保证？

上面我们说到， skiplist 插入一个节点时随机出一个层数，听起来怎么这么随意，如何保证搜索时

的效率呢？这里首先要细节分析的是这个随机层数是怎么来的。一般跳表会设计一个最大层数maxLevel 的限制，其次会设置一个多增加一层的概率p 。那么计算这个随机层数的伪代码如下图：

在 Redis 的 skiplist 实现中，这两个参数的取值为：

p = 1/4

maxLevel = 32

根据前面 randomLevel() 的伪码，我们很容易看出，产生越高的节点层数，概率越低。定量的分析

如下：

节点层数至少为 1 。而大于 1 的节点层数，满足一个概率分布。

节点层数恰好等于 1 的概率为 1-p 。

节点层数大于等于 2 的概率为 p ，而节点层数恰好等于 2 的概率为 p(1-p) 。

节点层数大于等于 3 的概率为 p^2 ，而节点层数恰好等于 3 的概率为 p^2*(1-p) 。

节点层数大于等于 4 的概率为 p^3 ，而节点层数恰好等于 4 的概率为 p^3*(1-p) 。

因此，一个节点的平均层数（也即包含的平均指针数目），计算如下：

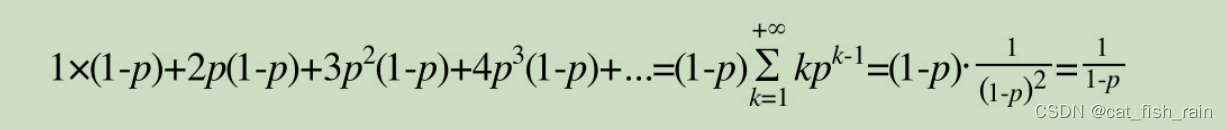
现在很容易计算出：

当p=1/2时，每个节点所包含的平均指针数目为2；
当p=1/4时，每个节点所包含的平均指针数目为1.33。
跳表的平均时间复杂度为 O(logN) ，这个推导的过程较为复杂，需要有一定的数据功底，有兴趣的老铁，可以参考以下文章中的讲解：

铁蕾大佬的博客： Redis内部数据结构详解(6)——skiplist - 铁蕾的个人博客

William_Pugh大佬的论文：ftp://ftp.cs.umd.edu/pub/skipLists/skiplists.pdf

3.skiplist的实现

力扣

#include <iostream>
#include <vector>
#include <algorithm>
#include <stack>
#include <map>
#include <ctime>
#include <queue>
#include <unordered_map>
#include <unordered_set>
#include <deque>
using namespace std;

void PrintVector2D(const vector<vector<int>> &array)
{

    for (const auto &row : array)
    {
        cout << "[";
        for_each(row.begin(), row.end(), [](int num)
                 { cout << num << " "; });
        cout << "]";
        cout << endl;
    }
}

struct ListNode
{
    int val;
    ListNode *next;
    ListNode() : val(0), next(nullptr) {}
    ListNode(int x) : val(x), next(nullptr) {}
    ListNode(int x, ListNode *next) : val(x), next(next) {}
};

struct TreeNode
{
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
    TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(nullptr), right(nullptr) {}
};

struct SkiplistNode
{
    int _val;
    vector<SkiplistNode *> _nextV;

    SkiplistNode(int val, int level) : _val(val), _nextV(level, nullptr) {}
};

class Skiplist
{
    typedef SkiplistNode Node;

public:
    Skiplist()
    {
        srand(time(0));
        _head = new SkiplistNode(-1, 1);
    }

    bool search(int target)
    {

        Node *cur = _head;
        int level = _head->_nextV.size() - 1;

        while (level >= 0)
        {

            //目标值比下一个节点值要打，向右走
            //下一个节点是空（尾）节点，目标值比下一个节点要小，向下走
            if (cur->_nextV[level] && cur->_nextV[level]->_val < target)
            {
                cur = cur->_nextV[level];
            }
            else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val > target)
            {
                --level;
            }
            else
            {
                return true;
            }
        }
        return false;
    }

    vector<Node *> FindPrevNode(int num)
    {

        Node *cur = _head;
        int level = _head->_nextV.size() - 1;

        vector<Node *> prevV(level + 1, _head);

        while (level >= 0)
        {
            //目标值比下一个节点值大，向右走

            if (cur->_nextV[level] && cur->_nextV[level]->_val < num)
            {
                cur = cur->_nextV[level];
            }

            else if (cur->_nextV[level] == nullptr || cur->_nextV[level]->_val >= num)
            {
                prevV[level] = cur;
                --level;
            }
        }
        return prevV;
    }

    void add(int num)
    {

        vector<Node *> prevV = FindPrevNode(num);
        int n = RandomLevel();

        Node *newnode = new Node(num, n);

        if (n > _head->_nextV.size())
        {
            _head->_nextV.resize(n, nullptr);
            prevV.resize(n, _head);
        }

        for (size_t i = 0; i < n; i++)
        {
            newnode->_nextV[i] = prevV[i]->_nextV[i];
            prevV[i]->_nextV[i] = newnode;
        }
    }

    bool erase(int num)
    {

        vector<Node *> prevV = FindPrevNode(num);

        //下一层下一个不是val,val 不再表中

        if (prevV[0]->_nextV[0] == nullptr || prevV[0]->_nextV[0]->_val != num)
        {
            return false;
        }

        else
        {
            Node *del = prevV[0]->_nextV[0];

            for (size_t i = 0; i < del->_nextV.size(); i++)
            {

                prevV[i]->_nextV[i] = del->_nextV[i];
            }

            delete del;

            int i = _head->_nextV.size() - 1;
            while (i >= 0)
            {

                if (_head->_nextV[i] == nullptr)
                    --i;
                else
                    break;
            }
            _head->_nextV.resize(i + 1);
            return true;
        }
    }

    int RandomLevel()
    {
        size_t level = 1;
        while (rand() <= RAND_MAX * _p && level < _maxLevel)
        {
            ++level;
        }
        return level;
    }

    void Print()
    {

        Node *cur = _head;
        while (cur)
        {
            printf("%2d\n", cur->_val);
            for (auto e : cur->_nextV)
            {
                printf("%2s", "\u2193");
            }
            printf("\n");
            cur = cur->_nextV[0];
        }
    }

private:
    Node *_head;
    size_t _maxLevel = 32;
    double _p = 0.25;
};

int main()
{

    system("pause");
    return 0;
}