📋📋📋本文目录如下:⛳️⛳️⛳️
目录
1 概述
2 最优潮流
3 电力系统强大的CVX
4 直流电网中最优潮流(OPF)的凸优化
4.1 Matlab代码
4.2 运行结果
5 微电网中最优潮流(OPF)的凸优化
5.1 Matlab代码
5.2 结果
6 写在最后
💥💥💥💞💞💞欢迎来到本博客❤️❤️❤️💥💥💥

1 概述
微电网有望在未来的智能电网概念中发挥基本作用。特别是直流微电网,由于其在效率、可靠性和可控性方面的优势,正获得越来越多的关注。直流微电网由于没有无功功率或频率控制,因此可以实现高效率和简化控制;由于具有孤岛运行的能力,因此可以实现高可靠性;由于许多发电和存储技术已经是直流的(如太阳能光伏发电、电池),因此可以实现简单的集成。此外,大多数家用电器可以适应直流操作。在一个典型的直流微电网中,电力电子转换器可以作为恒定电流或恒定功率运行。在后一种情况下,电网的模型变成了非线性的,需要用功率流算法进行静止状态分析。这个问题是非线性/非凸性的,需要用数值算法来解决。当然,由于问题的非线性性质,这类算法的收敛性并不总是得到保证。一个算法甚至可能发散或趋向于一个不现实的解决方案。
2 最优潮流
最优潮流(OPF)是指在满足电网约束的同时,以最小的成本将负荷分配给电厂。描述为在满足网络(潮流)约束的情况下最小化所有承诺的工厂的总燃料成本的优化问题。
更多知识点查看:最优潮流
3 电力系统强大的CVX
本文程序需要安装CVX,我在前面的文章对这一强大工具进行讲解:
电力系统强大的CVX学习(Matlab&Python)
4 直流电网中最优潮流(OPF)的凸优化
4.1 Matlab代码
%% 直流电网中最优潮流(OPF)的凸优化
clc
clear all
Vnom = 400E3;
Pnom = 1E9;
Znom = Vnom*Vnom/Pnom;
%% 线路数据
% N1 N2 Ohm
Lines =[1 2 3.42
2 3 2.28
2 4 5.70
3 4 4.56
4 5 1.90
3 6 1.90
5 6 2.85];
Lines(:,3) = Lines(:,3)/Znom; % in pu
%% 节点数据
% Node Pmin(kW) Pmax(MW) Droop(pu)
Nodes =[1 -2400 2400 0.50
2 0 0 0.00
3 -2400 2400 0.50
4 -2400 2400 0.50
5 800 800 0.00
6 1600 1600 0.00];
Nodes(:,2:3) = Nodes(:,2:3)*1E6/Pnom;
NumE = length(Lines(:,1)); %线路数
NumN = length(Nodes(:,1)); % 节点数
Pmin = Nodes(:,2);
Pmax = Nodes(:,3);
H = Nodes(:,4);
%% 矩阵G
G = zeros(NumN,NumN);
for k = 1:NumE
n1 = Lines(k,1);
n2 = Lines(k,2);
gkm = 1/(Lines(k,3));
G(n1,n1) = G(n1,n1) + gkm;
G(n2,n2) = G(n2,n2) + gkm;
G(n1,n2) = G(n1,n2) - gkm;
G(n2,n1) = G(n2,n1) - gkm;
end
%不考虑松弛节点,因此节点数等于线数,因为网格是径向的。
U = ones(NumE,1);
%% 电力系统强大的求解器CVX
cvx_begin
variable V(NumN);
variable P(NumN);
minimize (V'*G*V);
subject to
P == G*V-sum(G)' + V.*sum(G)';
P <= Pmax;
P >= Pmin;
V >= 0.9;
cvx_end
[V, P]
%
U = ones(NumN,1);
V = U;
P = diag(V)*(G*V)+H.*(U-V);
tic
for k = 1:10
cvx_begin quiet
variable dV(NumN);
variable dP(NumN);
minimize ((V+dV)'*G*(V+dV));
subject to
-[diag(H)-diag(V)*G-diag(G*V)]*dV == dP;
P+dP-H.*(U-V)+H.*dV <= Pmax;
P+dP-H.*(U-V)+H.*dV >= Pmin;
V+dV >= 0.9;
V+dV <= 1.1;
cvx_end
if norm([dV;dP])<1E-5
break
end
disp('-----------------------------------------------');
disp(k);
disp(cvx_status);
disp(cvx_optval);
V = V + dV;
P = diag(V)*(G*V)+H.*(U-V);
disp([dV, dP, V, P])%
gr(k) = cvx_optval;
end
toc
%% 可视化
plot(gr,'Color','r','Marker','*','LineWidth',2);
grid on;4.2 运行结果

5 微电网中最优潮流(OPF)的凸优化
5.1 Matlab代码
%% 微电网中最优潮流(OPF)的凸优化
clc
clear all
R = 1.5E-3;
Vnom = 380;
Pnom = 1000;
Znom = Vnom*Vnom/Pnom;
%% 线路数据
% N1 N2 lenght(m)
Lines =[1 2 50
2 3 15
2 4 20
4 5 18
2 6 23
6 7 17
7 8 21
7 9 13
8 10 15];
Lines(:,3) = Lines(:,3)*R/Znom; % in pu
%% 节点数据
% Node Pmin(kW) Pmax(kW) Droop(pu)
Nodes =[1 0.00 0.00 0.00
2 -10.00 -7.50 0.50
3 -10.00 -6.30 0.60
4 0.00 10.00 0.50
5 -10.00 -8.00 0.50
6 -10.00 -9.00 0.60
7 0.00 9.00 0.50
8 0.00 9.00 0.60
9 0.00 9.00 0.50
10 -10.00 -5.50 0.60];
Nodes(:,2:3) = Nodes(:,2:3)/Pnom*1000;
NumE = length(Lines(:,1)); % 线路数
NumN = length(Nodes(:,1)); % 节点数
Pmin = Nodes(:,2);
Pmax = Nodes(:,3);
H = Nodes(:,4);
%% 矩阵G
G = zeros(NumN,NumN);
for k = 1:NumE
n1 = Lines(k,1);
n2 = Lines(k,2);
gkm = 1/(Lines(k,3));
G(n1,n1) = G(n1,n1) + gkm;
G(n2,n2) = G(n2,n2) + gkm;
G(n1,n2) = G(n1,n2) - gkm;
G(n2,n1) = G(n2,n1) - gkm;
end
%不考虑松弛节点,因此节点数等于线数,因为网格是径向的。
U = ones(NumE,1);
%% 电力系统强大的求解器CVX
cvx_begin
variable V(NumN);
variable P(NumN);
minimize (V'*G*V);
subject to
P == G*V-sum(G)' + V.*sum(G)';
P <= Pmax;
P >= Pmin;
V >= 0.9;
cvx_end
[V, P]
%
U = ones(NumN,1);
V = U;
P = diag(V)*(G*V)+H.*(U-V);
for k = 1:10
cvx_begin quiet
variable dV(NumN);
variable dP(NumN);
minimize ((V+dV)'*G*(V+dV));
subject to
-[diag(H)-diag(V)*G-diag(G*V)]*dV == dP;
P+dP-H.*(U-V)+H.*dV <= Pmax;
P+dP-H.*(U-V)+H.*dV >= Pmin;
V+dV >= 0.9;
V+dV <= 1.1;
cvx_end
if norm([dV;dP])<1E-4
break
end
disp('-----------------------------------------------');
disp(k);
disp(cvx_status);
disp(cvx_optval);
V = V + dV;
P = diag(V)*(G*V)+H.*(U-V);
disp([dV, dP, V, P])
gr(k) = cvx_optval;
end
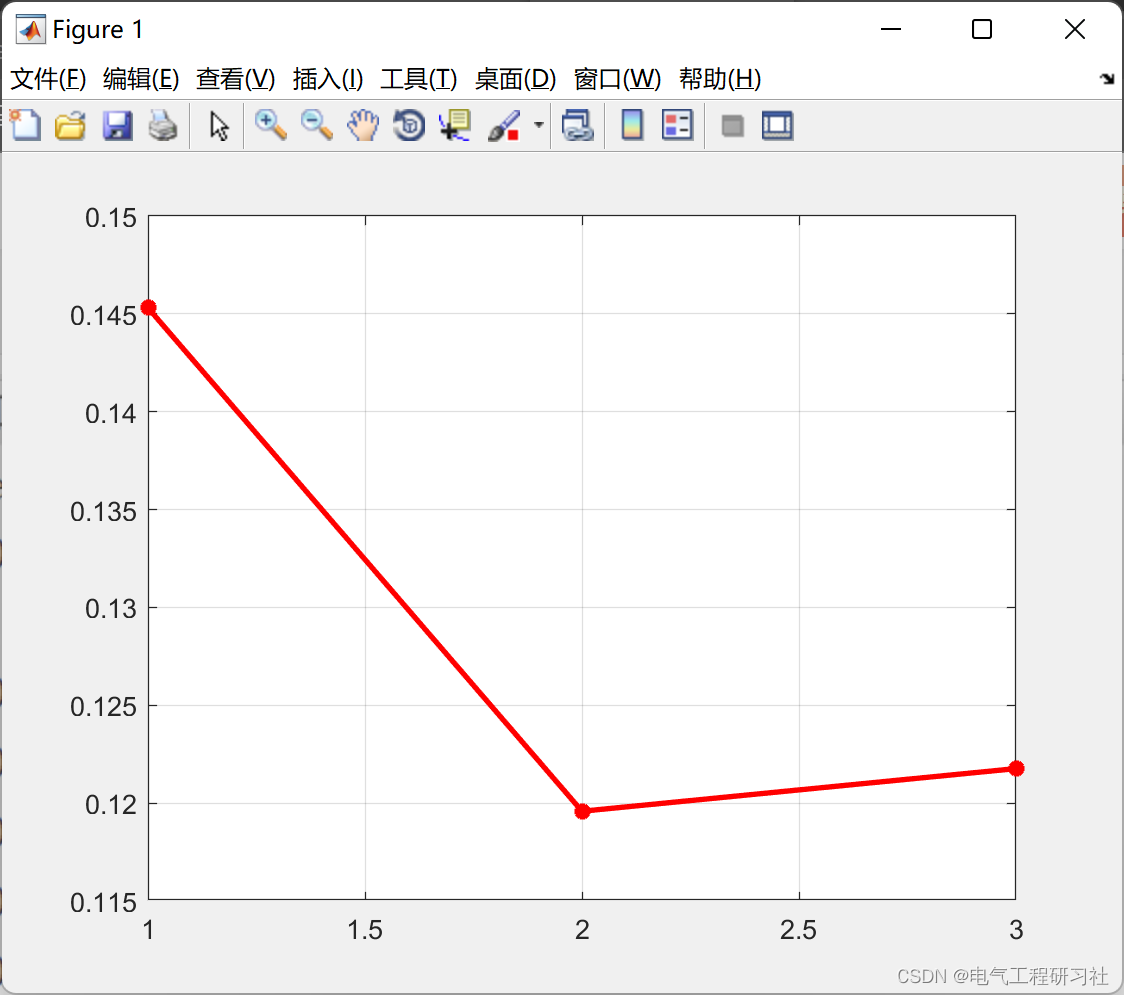
%% 可视化
plot(gr,'Color','r','Marker','*','LineWidth',2);
grid on;5.2 结果

6 写在最后
部分理论引用网络文献,若有侵权请联系博主删除。