经典假设

1、左右视图成功匹配的窗口，具有相同的像素

这个是最经典的假设，几乎所有视差图计算都用上了他，通过匹配左右窗口像素，得到最佳匹配对应的x轴坐标差，就是视差

2、像素P的视差只与其领域有关

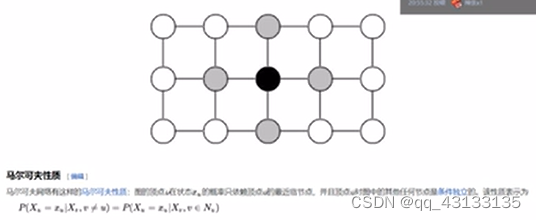
这个是基于马尔可夫性质，做代价聚合的时候，基于这个假设就用周围的像素视差对中间的视差进行聚合。

3、相近颜色的点具有相近的视差

如果一个平面只采集到几个有效视差，就可以基于这个假设，拟合一个平面去确定其他位置的视差。

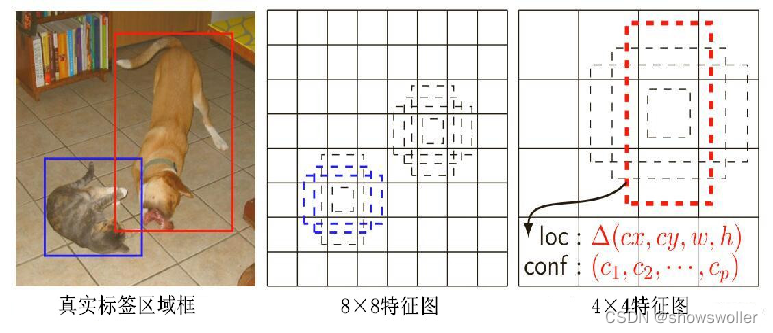
4、视差非连续区，应具有颜色差或亮度差

如上图的边界区，就是视差不连续的

上述这些假设都作为各类算法的切入点，详细可以观看 立体匹配理论与实战

立体匹配

一般分为四种：局部、全局、半全局、基于深度学习的匹配，前三种都是传统的算法。

代价计算

如经典的SDA匹配，使用左视图的窗口减去右视图的窗口，得到SDA值最小很可能就是真实视差。不过这样计算出来的一般都比较粗糙，我们一般只用来做初始代价计算，然后得到DSI（视差空间影像），这是一个三维数组（尺寸是w×h×d），其深度d代表视差，我们在每个候选视差位置计算得到的代价就填入该数组（可以用于后续的代价聚合）：

代价聚合

就是用周围像素的代价聚合到中间去，方法很多，什么双边滤波，置信权重，交叉线，扫描线等等。像SGM之类的就用来这个，效果不错。

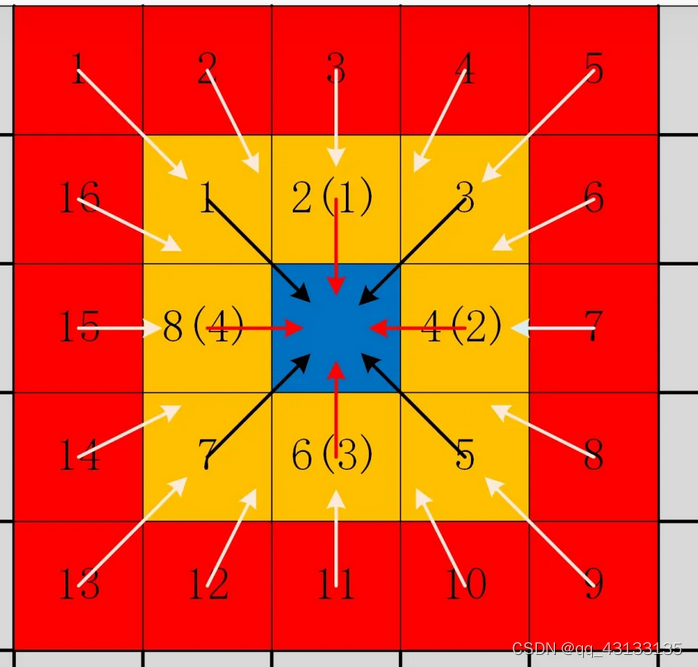
视差估计

聚合完用赢家通吃，得到最佳视差。当然如果直接用全局视差估计方法，比如图割，则不需要进行聚合，DSI计算完直接进行图割即可，不过全局方法会比较慢就是了。

视差优化

比如左右一致性检查的话，分别求出左右图像的视差，若同一个目标位置视差不一致则剔除。

再比如小连通域剔除，比如有一些散落的小白点，可以通过这个方法剔除这种错误

最后可以用平滑滤波，中值滤波这种去一下噪声。

结尾