用vit的时候读了一下transformer的思想,前几天面试结束之后发现对QKV又有点忘记了, 写一篇文章来记录一下
参考链接: 哔哩哔哩:在线激情讲解transformer&Attention注意力机制(上)在线激情讲解transformer&Attention注意力机制(上)_哔哩哔哩_bilibili
Attention is all you need介绍
更具体的介绍可以去阅读论文
在Attention is all you need这篇文章中提出了著名的Transformer模型
Transformer中抛弃了传统的CNN和RNN,整个网络结构完全是由Attention机制组成。
更准确地讲,Transformer由且仅由self-Attenion和Feed Forward Neural Network组成。
一个基于Transformer的可训练的神经网络可以通过堆叠Transformer的形式进行搭建,作者的实验是通过搭建编码器和解码器各6层,总共12层的Encoder-Decoder,并在机器翻译中取得了BLEU值得新高。
Attenion机制
在深度学习中,注意力机制的目标是从大量的信息中选择出更有用的信息。
而Attention is all you need这篇文章体现注意力机制的核心就是下面这个公式了
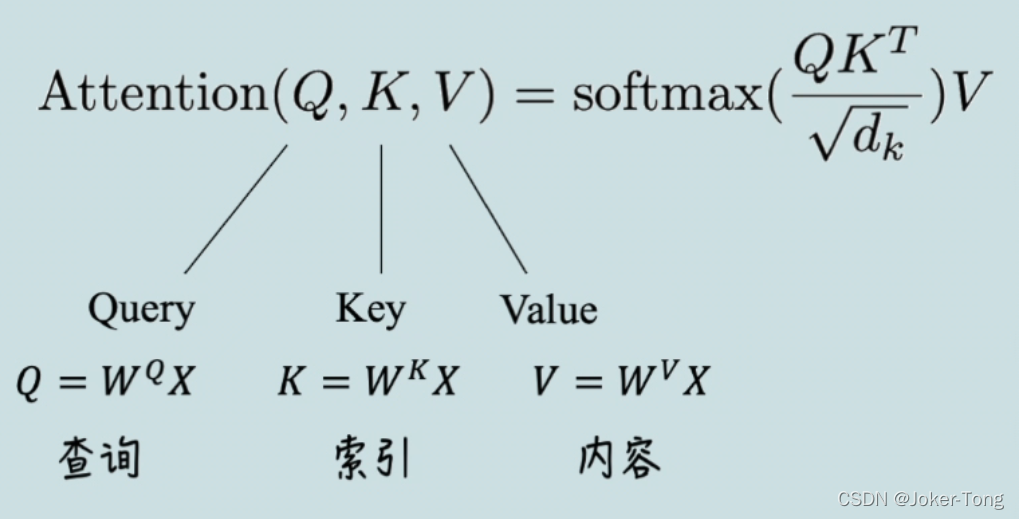
刚刚看到这个公式的时候我也是很蒙的,查了很多资料才搞懂,这里再次推荐一个B站的up主,讲的很形象, 本文的素材也是部分来自于此
在线激情讲解transformer&Attention注意力机制(上) 在线激情讲解transformer&Attention注意力机制(上)_哔哩哔哩_bilibili
Q,K,V是由输入的词向量x经过线性变换得到的,其中各个矩阵w可以经过学习得到, 这种变换可以提升模型的拟合能力, 得到的Q,K,V 可以理解为
Q: 要查询的信息
K: 被查询的向量
V: 查询得到的值
总结一下:
首先Q、K、V都源于输入特征本身,是根据输入特征产生的向量,但目前我们现在无需关注是如何产生这组向量的。
V可以看做表示单个输入特征的向量。当我们直接把一组V输入到网络中进行训练,那这个网络就是没有引入Attention机制的网络。
但如果引入Attention,就需要将这组V分别乘以一组权重α \alphaα,那么就可以做到有重点性地关注输入特征,如同人的注意力一般。
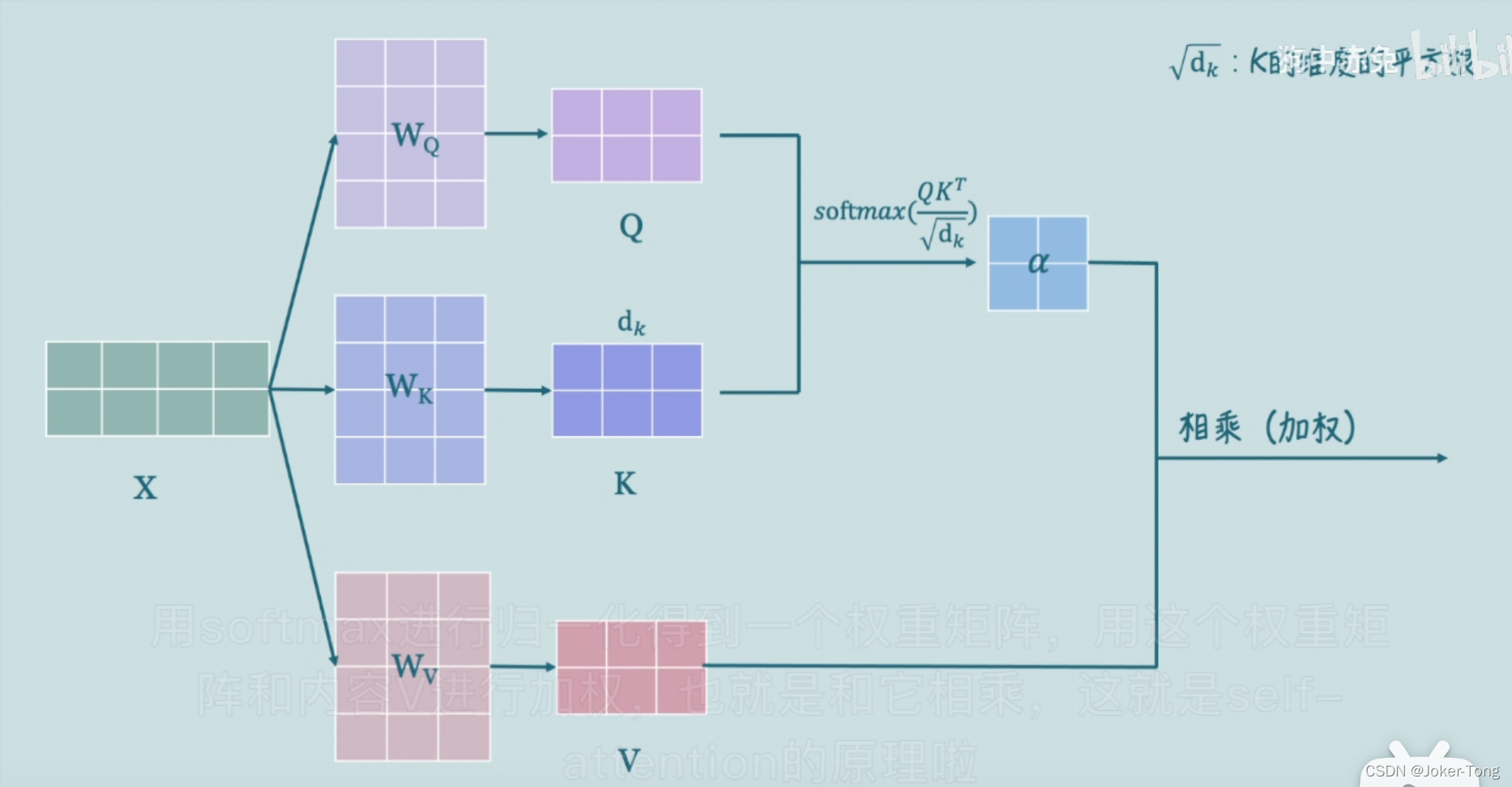
下面就用一个通俗的例子来解释如何学习到α \alphaα并且使用attention机制
通俗易懂的例子 海王与备胎
有一个海王,有N个备胎,他想要从自己的备胎中寻找出最符合自己期望的那个,便于他分配注意力并且来管理时间。
在这个案例中
Q 表示渣男对备胎的要求
K 表示渣男自身的条件 因为备胎们也会看渣男的条件是否让她们满意
V 表示匹配的结果
无论是渣男还是备胎, 都有着自己的一套Q K V 来记录他们选择的情况

现在我们的渣男要开始筛选备胎了, 对他来说,当然是备胎的条件越符合他的理想越好
放在Q,K,V上来讲就是渣男的Q与备胎的K之间的相似度越高越好
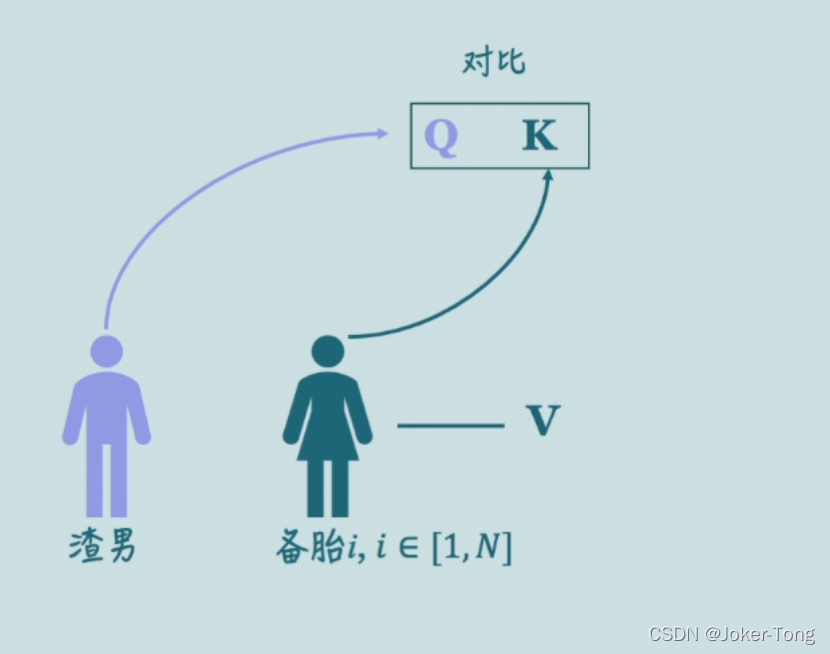
现在的问题就是如何计算他们的相似度了
点乘拓展:
在向量中,AB点乘的结果反应了他们之间的相似度, (A在B上的投影与B的模相乘得到的结果)
如果AB垂直,那么他们点乘为0, 也就是他们的相似度为0
因此AB点乘的结果越大, 我们就可以认为两个向量的相似度越高
在渣男选择备胎的过程中, 由于他们选择的条件Q,K是矩阵的形式, 因此计算矩阵之间的相似度我们采用 来实现
相当于计算了Q的每一行与K的每一行的点乘结果(结合下图中2行3列的例子来理解) 也就得到了Q的每一行与K的每一行之间的相似度结果
最后通过softmax来进行归一化, 得到一个直观的0~1之间的相似度结果
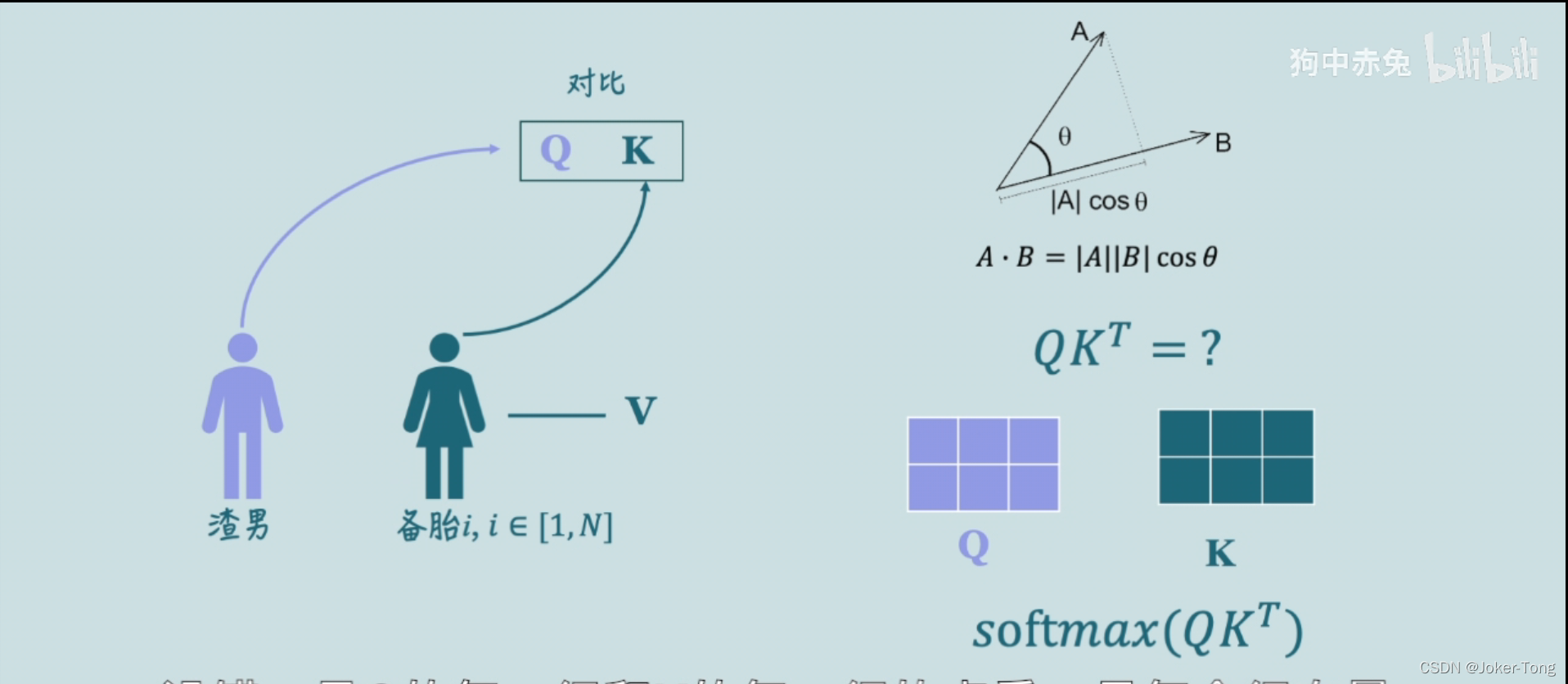
渣男与备胎之间的这些结果共同构成了权值, 也就是核心式中的左半部分。
对于也许很多人会有疑问,为什么要除以
,能不能除以其他的东西呢,为什么是除不是乘呢? 主要原因如下
1. 首先要除以一个数,防止输入softmax的值过大,导致偏导数趋近于0;(另一个角度来看: 如果权重矩阵里面有0.9这种高注意力的权重,那么会导致注意力几乎都被它所分走,除以一个数可以让注意力的分布更加均匀)
2. 是词向量/隐藏层的维度, 选择
可以使得q*k的符合N(0,1)的分布,类似于归一化。
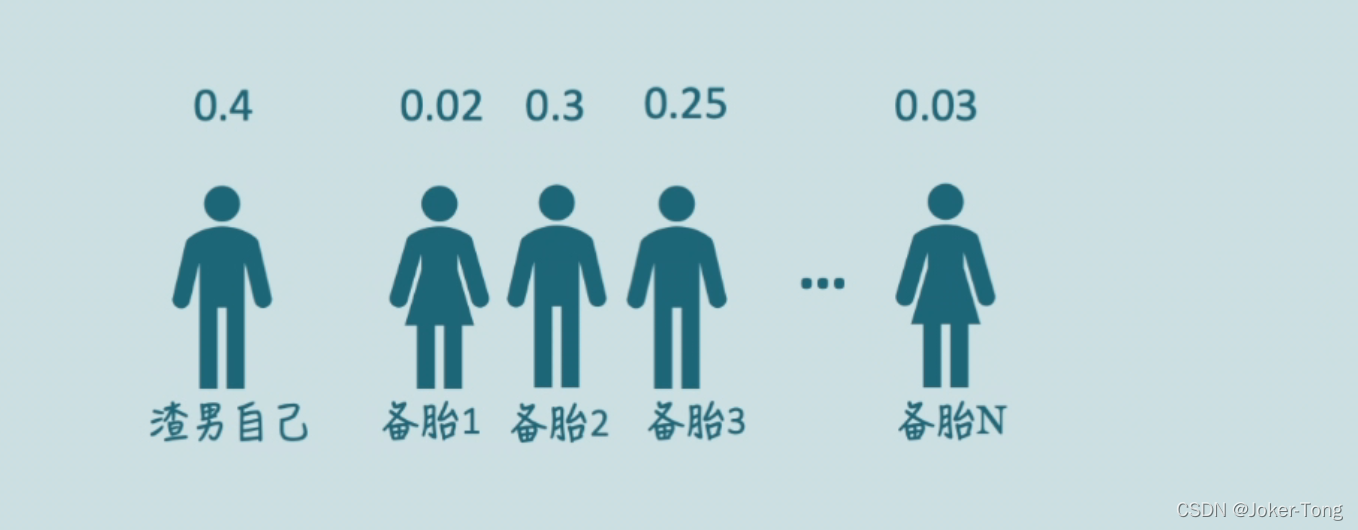
利用上面计算后得到的权重矩阵来对每个备胎加权,也就是
A t t e n t i o n ( K , Q , V ) = α ∗ V
这样渣男就知道自己该对谁付出更多的注意力了,也有可能渣男比较自恋, 备胎都不太满足他的要求, 他的理想型可能是自己这种类型的, 那么他最需要关注的就是他自己
原文链接:https://blog.csdn.net/Weary_PJ/article/details/123531732

![[附源码]Python计算机毕业设计Django疫情期间小学生作业线上管理系统](https://img-blog.csdnimg.cn/31597253376a4e3084e85db5cdd0d6e4.png)

![[附源码]Python计算机毕业设计Django智能家电商城](https://img-blog.csdnimg.cn/71c136aab6b3465a8d2c8bf67061f916.png)









![[附源码]Python计算机毕业设计Django在线教育系统](https://img-blog.csdnimg.cn/d9d8c81e2a1b4367b2e5d03d343be793.png)