一、MATLAB简介
- MATLAB(Matrix Laboratory, 即矩阵实验室)是MathWork公司推出的一套高效率的数值计算和可视化软件.
- MATLAB是当今科学界最具影响力、也是最具活力的软件, 它起源于矩阵运算, 并已经发展成一种高度集成的计算机语言.
- 它提供了强大的科学运算、灵活的程序设计流程、高质量的图形可视化与界面设计、便捷的与其他程序和语言接口的功能.
A. MATLAB发展简史
1、 MATLAB的开发单位:
美国Mathworks公司,Cleve Moler博士
2、几个不同的发展时期
- 70年代末,Cleve Moler为讲授矩阵理论和数据分析编写了Linpack与Eispack软件包。
- 1984年,成立公司Mathworks,推出第二代MATLAB。内核用C编写。
- 1990年,推出系统仿真工具Simulink。
- 1993年,Matlab 4.0——Windows版。
- 1994年,Matlab 4.2——开始广受重视和应用。
- 1999年,Matlab 5.3——32位运算。
- 2000年11月,Matlab 6.0。
- 2001年5月,Matlab 6.1。
- 2002年8月,matlab 6.5—— 加入JIT加速器。
B. MATLAB的特点
- 一个变量可以直接当作一个矩阵。
- 一个元素可以直接当作一个复数。
- 用解释方式对程序加以执行。
- 数据可以通过MATLAB绘图功能实现可视化,最复杂的可视效果可以是三维坐标中的立体曲面图。
- 不仅能进行数值运算,还能进行符号运算及系统仿真。
- 有多达30多个工具箱。
- 与其他语言程序或应用程序有方便的接口。例如:C、Fortran、Word等。
- 大量繁杂的数学运算和分析可调用MATLAB的函数直接求解。
- “教育部全国计算机专业课程指导委员会”已将MATLAB作为推荐课程。
- MATLAB建立在C/C++语言基础之上, 抽象程度更高, 也更加接近人类的自然语言, 因而在编写程序时可以更多关注问题的整体处理上, 而不是数据的细节处理.
- MATLAB内置了大量的函数, 用户可以直接使用而不需要再自己编写. 由于MATLAB设计的开放性, 许多领域的专家都为MATLAB编写了各种程序工具箱. 这些工具箱提供了用户在特别应用领域所需的许多函数, 这使得用户不必花大量的时间编写程序就可以直接调用这些函数, 达到事半功倍的效果.
- MATLAB使用非常简洁的语句来表达丰富的含义, 简单易懂, 与C/C++等高级程序设计语言相比代码量少很多, 因而编程速度快, 非常适合做数学运算.
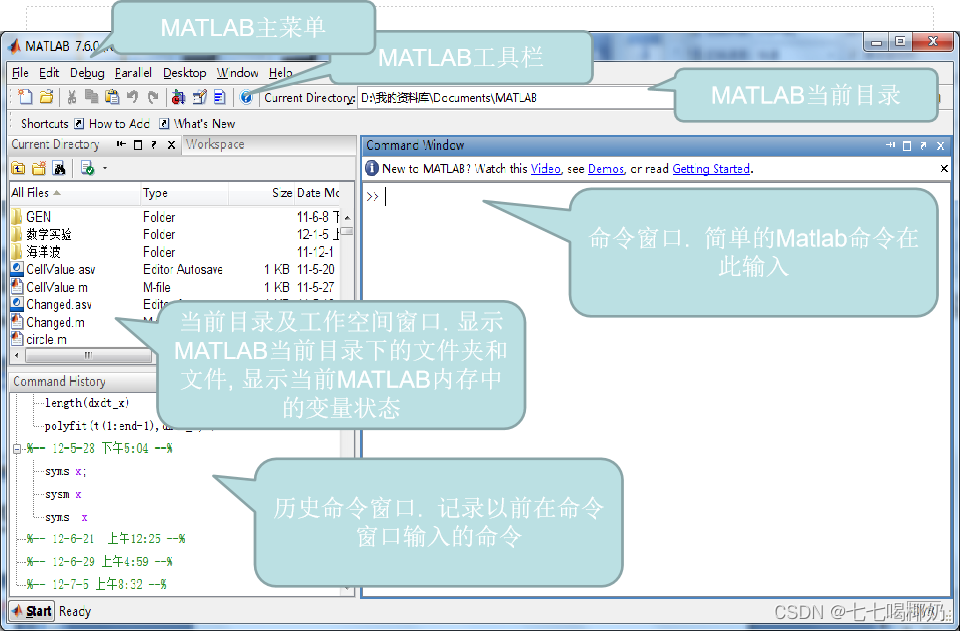
二、 MATLAB基本语法
- MATLAB的基本运算对象是数组(矩阵), 即使是1个数也当作一个1×1的矩阵来看待;
- MATLAB语法与其它高级程序设计语言相似, 符合一般的书写习惯;
- MATLAB语句可以以分号来结束, 也可以不用. 若以分号结束,则在命令窗口中不显示计算结果, 否则显示结果;
- 变量无需预先定义, 可在需要时直接使用;
- MATLAB的代码区分大小写;
- 以%作为注释界定符.
1、数组的定义
a=5 %或 a=[5]
A=[2 0 4 1]
B=[4 1 6; 5 9 4; 3 1 2] %这是个3*3矩阵规则1:
以方括号为界定符, 元素之间用空格或逗号分隔, 两行之间用分号分隔; 各行元素个数必须相同;
A=1:10
B=1:3:10
C=10:-1:1
X=linspace(-pi,pi,50)
对应的:
A=[1 2 3 4 5 6 7 8 9 10]
B=[1 4 7 10]
C=[10 9 8 7 6 5 4 3 2 1]
X=[-3.1416 -3.0134 -2.8851 ... 2.8851 3.0134 3.1416]
规则2:
- 产生等差数列使用a:s:b, 从a开始, 步长为s, 最后一个数不超过b;
- linspace(a,b,n)产生n个数, 将区间[a,b]分成n-1等份.
A=zeros(3,3) %全零
B=ones(3,3) %全一
C=eye(3,3) %单位矩阵
规则3:
特殊矩阵由相应的命令生成, 行数和列数在参数中指定.
A=rand(3,3) %0~1均匀分布随机数矩阵
B=1+9*rand(3,3) %1~10均匀分布随机数矩阵
C=randn(3,3) %标准正态分布随机数矩阵
规则4:
- a~b均匀分布随机数矩阵使用a+(b-a)*rand(m,n);
- a为期望b为方差的正态分布随机数矩阵使用a+b*randn(m,n).
2、数组元素的存取操作
A(1) %这个是取向量中的第一个元素
B(1,2) %第一行第二列元素
B(1,:) %这是第一行所有矩阵
B(:,1)
B(2:3,1:2)
规则:
- 取向量的元素使用A(n);
- 取矩阵的元素使用A(m,n);
- 取子矩阵使用A(m1:m2,n1:n2);
- 表示“所有” 使用“:”
- 使用size(A)来获取 数组 A的行数和列数
>> A=[1 3 5 7 9]
A =
1 3 5 7 9
>> A(2)
ans =
3
>> A(6)=11
A =
1 3 5 7 9 11
>> A(1:end)
ans =
1 3 5 7 9 11
>> A(end:-1:1)
ans =
11 9 7 5 3 1
>> length(A)
ans =
6
>> A=eye(3,3)
A =
1 0 0
0 1 0
0 0 1
>> A(1,2)=2
A =
1 2 0
0 1 0
0 0 1
>> A(2,:)=[1 2 3]
A =
1 2 0
1 2 3
0 0 1
>> A(:,3)=A(:,2)
A =
1 2 2
1 2 2
0 0 0
>> size(A)
ans =
3 3
3、算术运算
A+B
A-B
%矩阵运算,如果参与运算的变量中有一个是标量, 则MATLAB将标量扩展成维数相同的矩阵, 与另一矩阵做运算
A*B
A/B
A\B
A^2
%数组运算
A.*B %A与B元素对应相乘
A./B %A与B元素对应相除
A.^2 %A的元素和平方4 、数组变形
1.C=[A B]
![]()
2.C=[A;B]
![]()
4.C=A’
![]()
4.C=repmat(A,m,n)
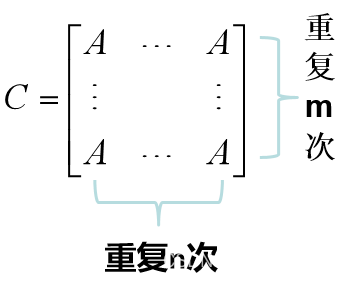
5.C=A(:) %将A的所有元素排成一列
6.A(1,:)=[] %删除A的第1行
>> A=eye(2,2) %产生2阶单位矩阵
A =
1 0
0 1
>> B=rand(2,2) %产生2阶随机数矩阵
B =
0.9649 0.9706
0.1576 0.9572
>> C=[A B] %矩阵横向合并
C =
1.0000 0 0.9649 0.9706
0 1.0000 0.1576 0.9572
>> C=[A;B] %矩阵纵向合并
C =
1.0000 0
0 1.0000
0.9649 0.9706
0.1576 0.9572
>> C=A’ %矩阵转置
C =
1 0
0 1
>> C=repmat(A,1,2) %矩阵重复
C =
1 0 1 0
0 1 0 1
>> C=A(:) %排成一列
C =
1
0
0
1
>> A(1,:)=[] %删除一行
A =
0 1
5、举例
解线性方程组
6x1+3x2+4x3=3
-2 x1+5 x2+7 x3=-4
8 x1-4 x2-3 x3=-7
A = [6 3 4; -2 5 7; 8 -4 -3]
B = [3;-4; -7]
X = A\B
X = A^(-1)*B
X = inv(A)*B
X = linsolve(A,B)
得到:
X =
0.6000
7.0000
-5.4000
6、常用函数
| 分类 | 函数名 | 意义 |
| 基本数学函数 | abs(x) | 实数的绝对值或复数的模 |
| sqrt(x) | 开平方 | |
| real(z) | 复数z的实部 | |
| imag(z) | 复数z的虚部 | |
| round(x) | 取整,四舍五入 | |
| fix(x) | 取整,无论正负,舍去小数至最近整数 | |
| floor(x) | 取整,舍去正小数至最近整数 | |
| ceil(x) | 取整,加入正小数至最近整数 | |
| exp(x) | 自然指数 | |
| pow2(x) | 2的指数 |
| 分类 | 函数名 | 意义 |
| 基本数学函数 | rem(x,y) | 求x除以y的馀数 |
| gcd(x,y) | 整数x和y的最大公因数 | |
| lcm(x,y) | 整数x和y的最小公倍数 | |
| log(x) | 以e为底的对数,即自然对数或 | |
| log2(x) | 以2为底的对数 | |
| log10(x) | 以10为底的对数 | |
| sign(x) | 符号函数. 当x<0时, sign(x)=-1; 当x=0时, sign(x)=0; 当x>0时, sign(x)=1. |
| 分类 | 函数名 | 意义 |
| 三角函数 | sin(x) | 正弦函数 |
| cos(x) | 余弦函数 | |
| tan(x) | 正切函数 | |
| asin(x) | 反正弦函数 | |
| acos(x) | 反余弦函数 | |
| atan(x) | 反正切函数 | |
| sinh(x) | 双曲正弦函数 | |
| cosh(x) | 双曲余弦函数 | |
| tanh(x) | 双曲正切函数 | |
| asinh(x) | 反双曲正弦函数 | |
| acosh(x) | 反双曲余弦函数 | |
| atanh(x) | 反双曲正切函数 |
| 分类 | 函数名 | 意义 |
| 杂项 | min(x) | 向量x的元素的最小值 |
| max(x) | 向量x的元素的最大值 | |
| mean(x) | 向量x的元素的平均值 | |
| diff(x) | 向量x的相邻元素的差 | |
| length(x) | 向量x的元素个数 | |
| size(x) | 数组元素个数 | |
| sort(x) | 对向量x的元素进行排序 | |
| norm(x) | 向量x的欧氏长度 | |
| sum(x) | 向量x的元素总和 | |
| prod(x) | 向量x的元素总乘积 | |
| cumsum(x) | 向量x的累计元素总和 |
| 分类 | 函数名 | 意义 |
| 矩阵计算 | det(A) | 矩阵行列式 |
| rank(A) | 矩阵的秩 | |
| inv(A) | 矩阵的逆 | |
| norm(A) | 矩阵范数 | |
| trace(A) | 矩阵的迹 | |
| eig(A) | 矩阵特征值和特征向量 | |
| rref(A) | 化为行阶梯形 | |
| cond(A) | 矩阵条件数 | |
| lu(A) | LU分解 | |
| chol(A) | Cholesky分解 |